
- •§1. Общее уравнение линий второго порядка. Приведение общего уравнения к простейшим уравнениям линий второго порядка
- •§2. Линии, определяемые общим уравнением линий второго порядка.
- •§3. Эллипс и его каноническое уравнение
- •§4.Исследования формы эллипса. Эксцентриситет эллипса.
- •§5.Директрисы эллипса и их свойства.
- •§6. Эллипс, как образ окружности при равномерном сжатии его диаметра. Параметрическое уравнение Эллипса
- •§7. Исследование форм гиперболы
- •§8. Исследование форм гиперболы.
- •§9. Эксцентриситет и директрисы гиперболы.
- •§10. Параметрическое уравнение гиперболы. Сопряжённые гиперболы
- •§11.Парабола и ее каноническое уравнение
- •§12.Общие определения эллипса, гиперболы и параболы через эксцентриситет.
- •§13.Полярное уравнение эллипса, гиперболы и параболы.
- •§14. Взаимное расположение прямой и линии 2го порядка. Асимптотическое направление. Классификация линий 2го порядка по их асимптотическим направлениям.
- •§15. Касательная и нормаль линии 2го порядка, их уравнения.
- •§16. Оптические свойства линий 2го порядка.
- •§17 Центр линий 2го порядка. Их классификация по характеру места центров.
- •§18 Диаметр, сопряженный данному неасимтотическому направлению. Сопряженные направления и диаметры. Особые и неособые направления.
- •§19 Главное направленние. Главный диаметр.
- •§20. Уравнение линий второго порядка, отнесенное к двум ее сопряженным диаметрам.
- •§21. Уравнение линий второго порядка в одск, если направление осей является главными.
- •§22.Определение канонического уравнения линии 2-го порядка при помощи ортогональных инвариантов.
- •§23. Таблица для определения вида линии 2-го порядка по ортогональным инвариантам.
- •§24. Построение центральной линии 2-го порядка заданной общим у-нием.
- •§27.Побудова лінії 2 порядку, як канонічний перетин.
§15. Касательная и нормаль линии 2го порядка, их уравнения.
Пусть относительно ОДСК задана линия 2го порядка общим уравнением вида:
2F(x;y)=a11x2+2a12xy+a22y2+
+2a13x+2a23y+a33=0
(1)
и пусть задана некоторая прямая
![]() (2).
(2).
В §14 исследовалось
взаимное расположение линии (1) и прямой
(2) и их общие точки находились из
уравнения: Lt2+2Mt+N=0
(3),
где L=a11l2+2a12lm+a22m2;
M=l(a11x0+a12y0+a13)+m(a12x0+a22y0+a23)=lF'x(x0;y0)+mF'y(x0;y0);
N=2F(x0;y0)
(4)
. Прямая асимптотического направления
(L≠0),
для которой уравнение (3) имеет 1 (двойной,
парный) корень, называется касательной
линией (1), а соответствующая этому точка
называется точкой касания. Пусть
M0(x0;y0)
в (1) – следовательно в уравнении (3) N=0
и (3): Lt2+2Mt=0
(5) ↔
 Поскольку
решение (5) - единственное, то М=0 и по (4)
получаем: lF'x(x0;y0)+mF'y(x0;y0)=0
(6).
Поскольку
решение (5) - единственное, то М=0 и по (4)
получаем: lF'x(x0;y0)+mF'y(x0;y0)=0
(6).
 Таким
образом доказали следующую теорему:
Теорема:
прямая (2)
является касательной к линии (1) в точке
М0(x0;y0)
↔, когда справедлива пропорция (7). В
предположении, что (7) имеет смысл и
задаёт неасимптотическое направление.
Заметим, что направление прямой (2)
берётся с точностью до колинеарности
вектора u={l,m},
т.е. характеризуется пропорцией l/m.
Таким образом координаты направления
вектора
Таким
образом доказали следующую теорему:
Теорема:
прямая (2)
является касательной к линии (1) в точке
М0(x0;y0)
↔, когда справедлива пропорция (7). В
предположении, что (7) имеет смысл и
задаёт неасимптотическое направление.
Заметим, что направление прямой (2)
берётся с точностью до колинеарности
вектора u={l,m},
т.е. характеризуется пропорцией l/m.
Таким образом координаты направления
вектора
![]() можно выразить следующим образом:
можно выразить следующим образом:
![]()
Тогда уравнение касательной имеет вид:
F'x(x0;y0)(x-x0)+F'y(x0;y0)(y-y0)=0 (9).
А уравнение нормали:
F'x(x0;y0)(y-y0)-F'y(x0;y0)(x-x0)=0 (10).
Если
![]() ,
то т. М0(x0;y0):
,
то т. М0(x0;y0):
![]()
Называется особой
точкой линии (1) и в ней касательной не
существует. Найдём уравнение касательной
для канонических уравнений линии 2го
порядка:1.)![]()
![]()
![]()
![]()
![]()
![]()
2.)
![]()
![]()
![]()
3.) y2=2px; Fx'=-p; Fy'=y;
-p(x-x0)+y0(y-y0)=0;
y0y=y02+px-px0=2px0; y0y=p(x+x0)
4.) x2-y2=0 (11). В этом случае линия состоит из 2х прямых: y=x,y=-x, пересекающихся в т. (0;0). Очевидно, уравнение (9) в т. (0;0) выполняется тождественно, а при (x0;y0)=(0;0) уравнение (9) даёт одну из прямых y=x,y=-x; но поскольку эти прямые являются прямыми асимптотами направления, то касательными они не могут быть. Таким образом (11) ни в одной точке отличной от (0;0) касания не имеет. Любая прямая проходящая через (0;0) будет касательной к (11) в этой точке.
5.) y2=1 (12) Линия (12) состоит из 2х параллельных прямых y=1,y=-1. Уравнение (9) даёт 1 из этих прямых, следовательно ни в одной точке линии (12) касательной не существует.
6.) y2=0 (13) Линия (13) состоит из 2х совпадающих прямых y=0. Уравнение (9) в этом случае удовлетворяется тождественно, следовательно любая прямая проходит через т. М0(х;0) и отличныая от y=0 является касательной к линии (13). Следовательно для линий 2го порядка распадающихся на пару прямых касательные существуют только в общих точках этих прямых и для любой такой точки каждая прямая проходящая через неё (отличная от данной) будет касательной. Последний вывод находится в некотором противоречии с общепринятым представлением о касательной. Если прямая имеет асимптоту направления (L=0), то уравнение (3) будет линейным и тогда 2Mt+N=0: 1.) если 1 корень, то прямая пересекает линию в 1 точке, но касательной не является;
2.) если не имеет корней, то прямая не имеет с линией ни одной общей точки;
3.) L=0, M=0, N=0: бесконечное число решений – прямая целиком принадлежит линии (1). Поскольку эти случаи рассматривают полностью полученное уравнение, то прямая имеющая 3 общие точки с линией – целиком в этой линии. Найдём условие при котором прямая Ax+By+C=0 (14) является касательной к эллипсу, гиперболе, параболе:
1.)![]() (15);M0(x0;y0)
принадлежит эллипсу, т.е.
(15);M0(x0;y0)
принадлежит эллипсу, т.е.
![]() (16).
Уравнение касательной к эллипсув этой
точке имеет вид:
(16).
Уравнение касательной к эллипсув этой
точке имеет вид:
![]() (17).
Тогда (17)
совпадает с (14) в случае:
(17).
Тогда (17)
совпадает с (14) в случае:
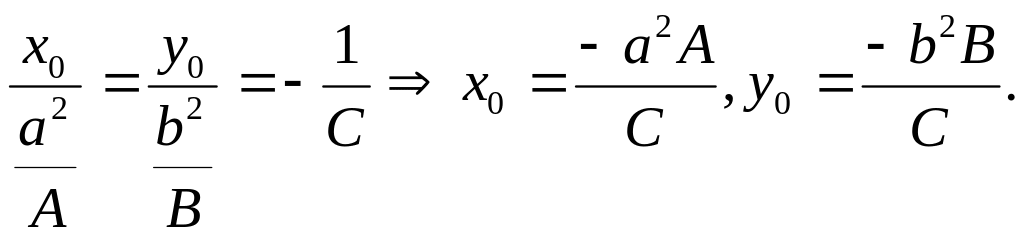
Подставим это в
(16), получим:
![]() (18)
(18)
(18) – критерий того, что (14) касательная к (15).
2.)![]() (19);
(19);![]() (20);
(20);![]() (21);
(21);

a2A2-b2B2=C2 (22). (22) Критерий того, что (14) касательная к параболе (19).
3.)y2=2px(23);
M0(x0;y0)→y20=2px0(24); y0y=p(x+x0);
-px+yy0-px0=0;
![]()
![]()
