§6. Эллипс, как образ окружности при равномерном сжатии его диаметра. Параметрическое уравнение Эллипса

Зобразимо на площині деяку пряму l

І нехай M дов. m площини

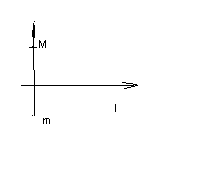
Поставимо у відповідність на m так що k- коефіцієнт стискання. Якщо l прийняти за Ox в ПДСК, то то

якщо то ми мємо розташування площини

Теорема

При рівномірному стисненні площини до d образом кола буде еліпс. Справедливе і протилежне. Кожен еліпс отримується як образ кола при рівномірному стиснені площини до d цього кола

Доведення

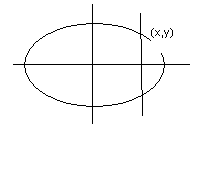
проведемо стиснення площини до Ox з k є (0,1) і нехай образом з

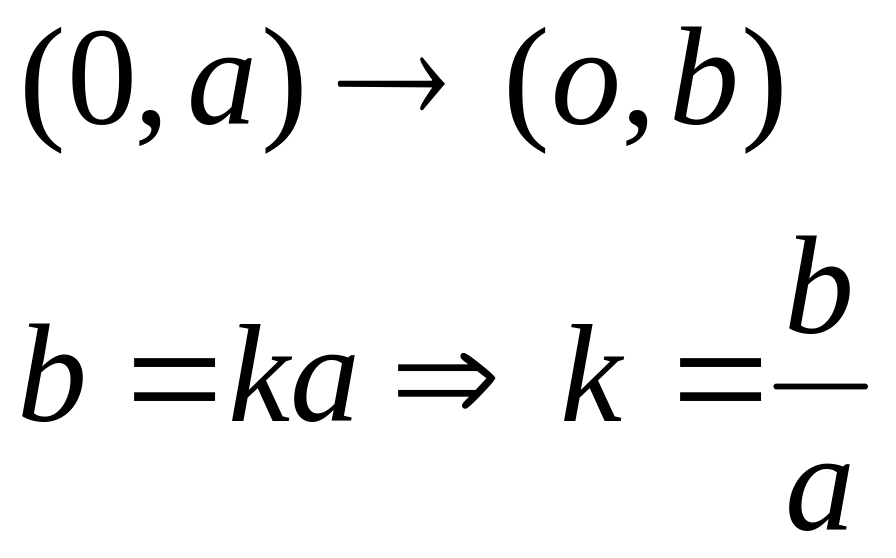
В цьому випадку будемо мати

Протилежне твердження доводиться аналогічно

Нехай M(x.y) є еліпсу а P(X.Y)

Позначимо через кут між Ob та Ox

параметричне рівняння еліпса

наз. ексцентричним кутом точки еліпса

§7. Исследование форм гиперболы

ПДСК на площині і нехай здана гіпербола

(1)

1)Оскільки в (1) x та y входять з парними степенями то якщо точка (x,y) належить гіперболі то і точки ( ) також належать гіперболі , таким чином осі координат є осями симетрії гіперболи

2)Із (1)- між прямими x=a та x=-a нема жодної точки гіперболи, таким чином вісь Oy не перетинається гіперболою ця вісь наз. умовною

Ox перетинається в двох точках - вершини гіперболи, а OX дійсна вісь

a-дійсна піввісь b-умовна піввісь

3)Знайдемо ГМТ гіперболи в першій чверті

а потім зобразимо симетрію відносно OX та OY

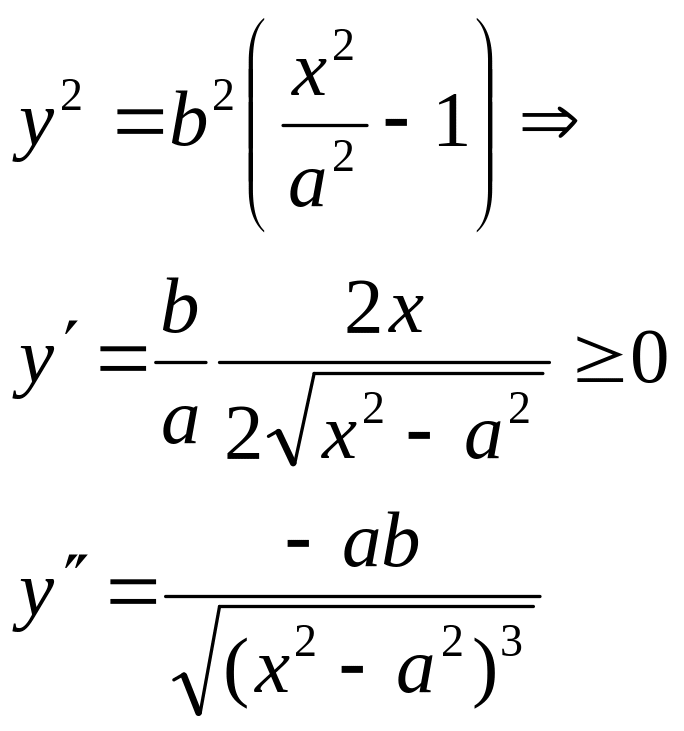
Асимптоти

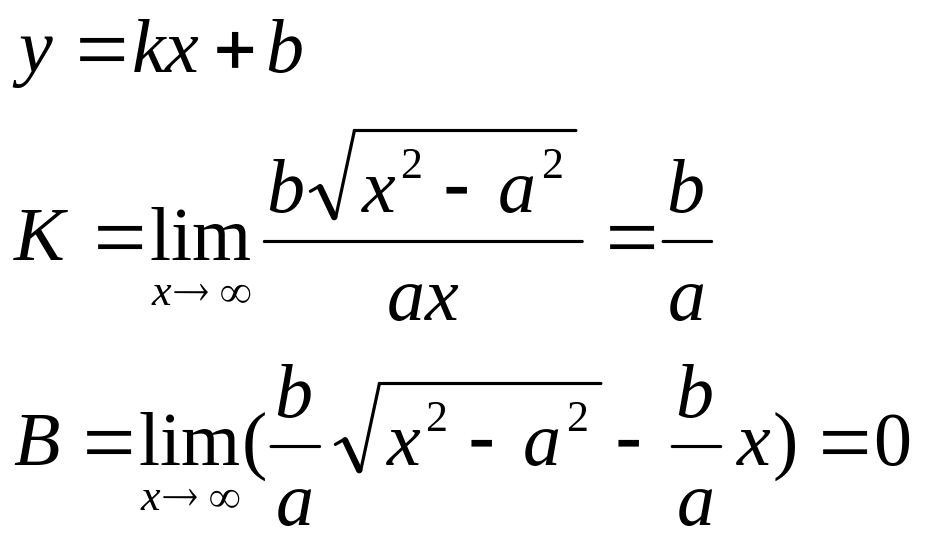
- асимптоти розташовані вище графіка

Парабола у якої піввісі – рівні називається рівносторонньою

§8. Исследование форм гиперболы.

Рассмотрим ПДСК, пусть имеем:

1) т.к. в (1) х и у входят с чётными степенями, то если т (х,у) лежит на гиперболе, то точки также лежат на гиперболе => (ОХ) и (ОУ) являются осями симметрии, а точка О является центром симметрии.

2) между прямыми х=а, х=-а нет ни одной точки гиперболы, т.е. ось ОУ не пересекает гиперболу и называется мнимой осью гиперболы.

А(-а,0), В(а,0) они называются вершинами гиперболы, а ОХ называют действительной осью гиперболы.

3) Найдем ГМТ гиперболы в 1 ой четверти, а затем сделаем симметрию относительно ОХ, ОУ, понятно, что у можно выразить через х.

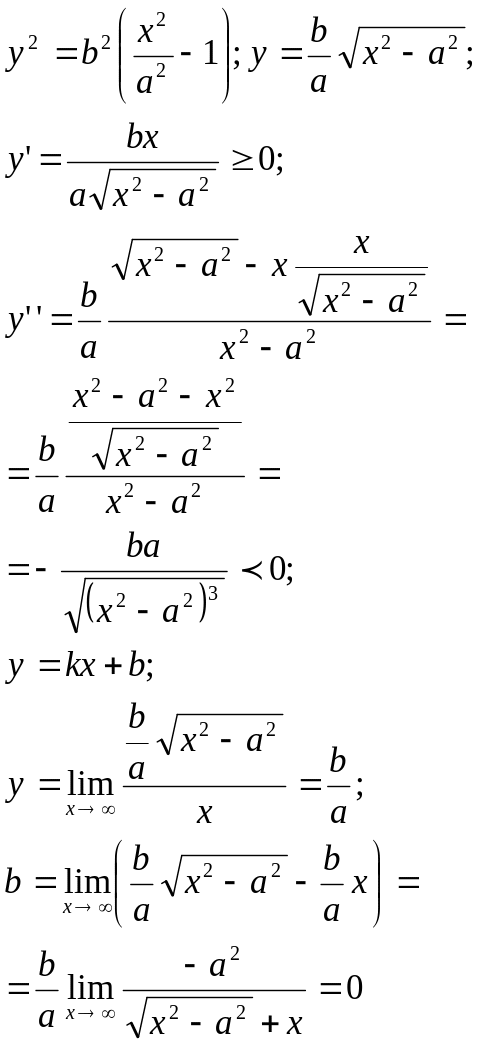
Гипербола имеет наклонную асимптоту , при этом поскольку асимптота лежит выше Гиперболы.

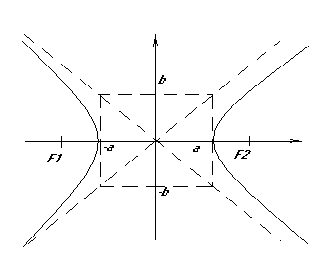
Гипербола, у которой полуоси равны называется раносторонней

Верно и обратное, если асимптоты взаимно перпендикулярны, то её полуоси равны.

§9. Эксцентриситет и директрисы гиперболы.

Отношением расстояний от центра гиперболы до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы.

Если гипербола задана уравением:

,то ксцентриситет:

Используя определение эксцентриситета имеем формулы:

Две прямые перпендикулярны к действительной оси гиперболы и отстающие от центра гиперболы на расстояние для гиперболы (1) они имеют вид:

, т.к. , то директрисы находятся между ветками гиперболы.

ТЕОРЕМА:

Для того, чтобы точка лежала на гиперболе необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса гиперболы к расстоянию от этой же точки до директрисы, соответствующего фокуса, было величиной постоянной, равной эксцентриситету гиперболы

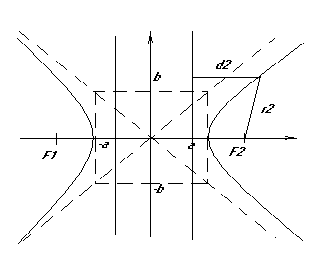
т.М принадлежит гиперболе т.и т.т., когда

Доказательство: проведём док-во для фокуса F2 и соотв. директрисе, для F2 док-во аналогично.Необходимость: пусть т. М лежит на гиперболе, докажем, что для неё выполняется (*).

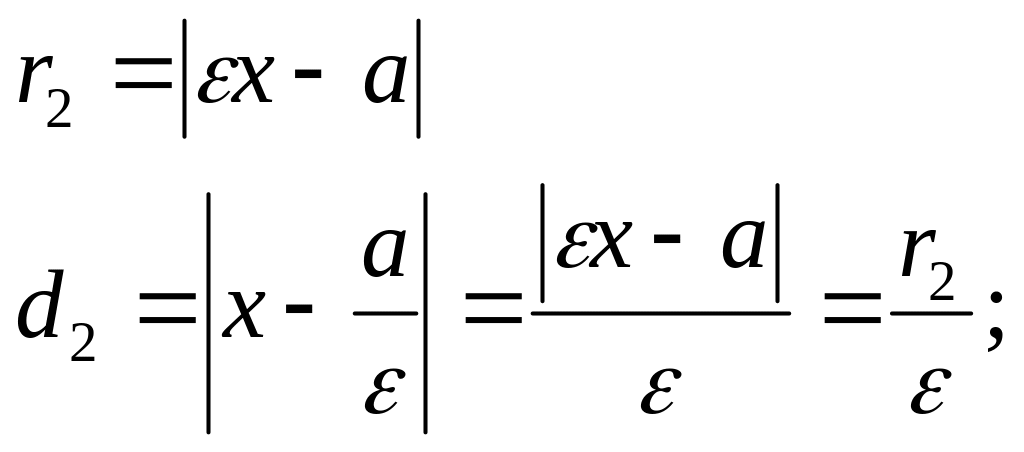
Достаточность:

Пусть для т. М выполняется (*), покажем, что она принадлежит гиперболе, поскольку:

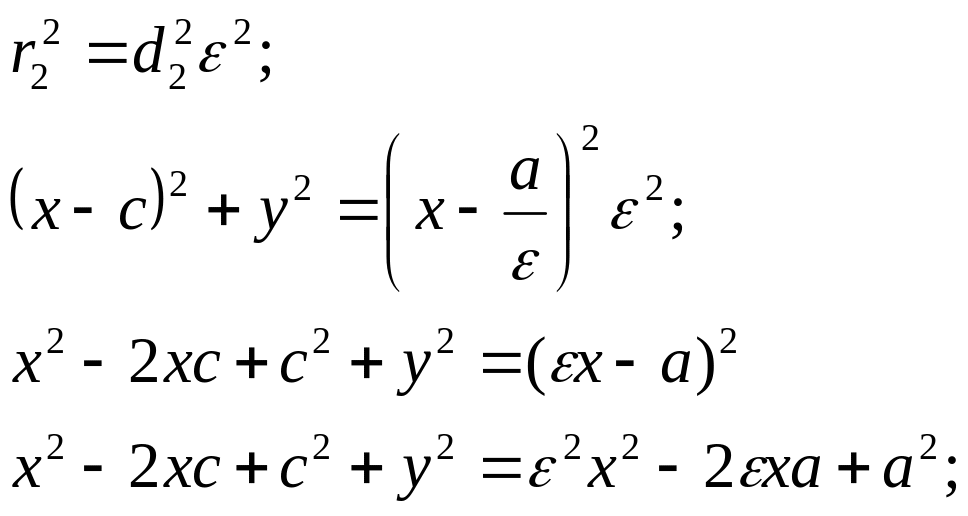
Заменим на своё выражение :

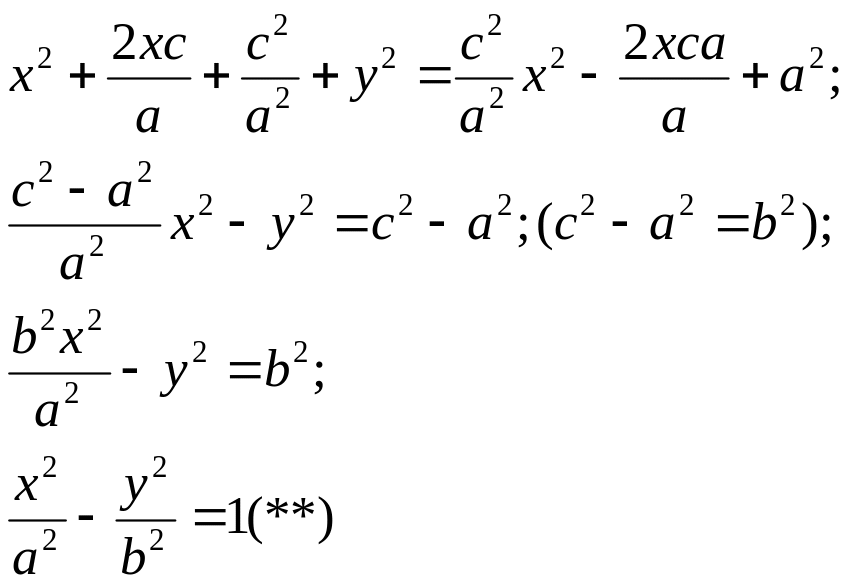Следовательно, т. М удовлетворяет уравнению (**), а значит лежит на гиперболе.

Обозначим расстояние от фокуса до директрисы через m, если заданы m и e(эксцентриситет), то можно всегда найти уравнение соответствующей гиперболы.

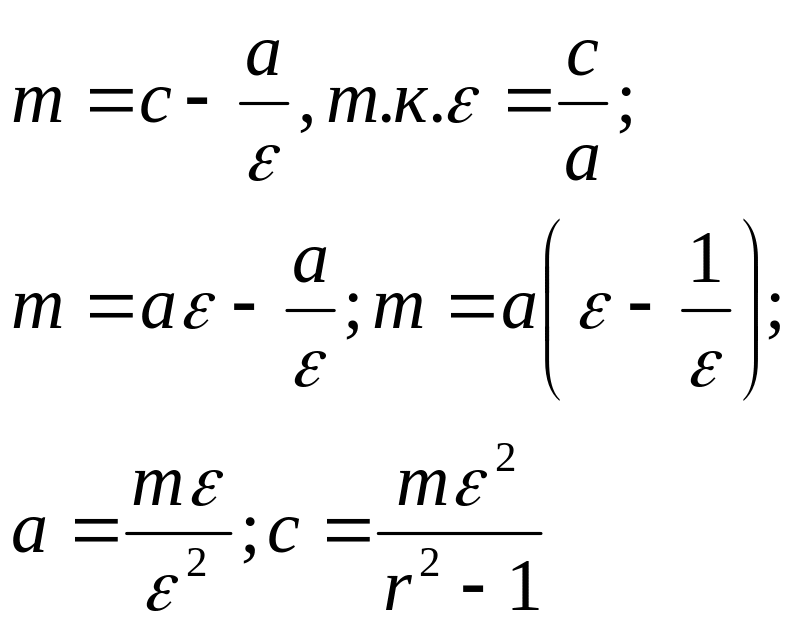
Если на плоскости заданы производные F и прямая d и , то всегда существует и при том только одна гипербола c заданными параметрами, следовательно, можно дать ещё одно определение гиперболы.

Гиперболой называется ГМТ на плоскости для каждой из которых отношение расстояния от данной точки к F до расстояния от данной точки к прямой d, не проходящих через F, есть величина постоянная, большая 1.