
- •§1. Общее уравнение линий второго порядка. Приведение общего уравнения к простейшим уравнениям линий второго порядка
- •§2. Линии, определяемые общим уравнением линий второго порядка.
- •§3. Эллипс и его каноническое уравнение
- •§4.Исследования формы эллипса. Эксцентриситет эллипса.
- •§5.Директрисы эллипса и их свойства.
- •§6. Эллипс, как образ окружности при равномерном сжатии его диаметра. Параметрическое уравнение Эллипса
- •§7. Исследование форм гиперболы
- •§8. Исследование форм гиперболы.
- •§9. Эксцентриситет и директрисы гиперболы.
- •§10. Параметрическое уравнение гиперболы. Сопряжённые гиперболы
- •§11.Парабола и ее каноническое уравнение
- •§12.Общие определения эллипса, гиперболы и параболы через эксцентриситет.
- •§13.Полярное уравнение эллипса, гиперболы и параболы.
- •§14. Взаимное расположение прямой и линии 2го порядка. Асимптотическое направление. Классификация линий 2го порядка по их асимптотическим направлениям.
- •§15. Касательная и нормаль линии 2го порядка, их уравнения.
- •§16. Оптические свойства линий 2го порядка.
- •§17 Центр линий 2го порядка. Их классификация по характеру места центров.
- •§18 Диаметр, сопряженный данному неасимтотическому направлению. Сопряженные направления и диаметры. Особые и неособые направления.
- •§19 Главное направленние. Главный диаметр.
- •§20. Уравнение линий второго порядка, отнесенное к двум ее сопряженным диаметрам.
- •§21. Уравнение линий второго порядка в одск, если направление осей является главными.
- •§22.Определение канонического уравнения линии 2-го порядка при помощи ортогональных инвариантов.
- •§23. Таблица для определения вида линии 2-го порядка по ортогональным инвариантам.
- •§24. Построение центральной линии 2-го порядка заданной общим у-нием.
- •§27.Побудова лінії 2 порядку, як канонічний перетин.
§1. Общее уравнение линий второго порядка. Приведение общего уравнения к простейшим уравнениям линий второго порядка
Линией второго
порядка называется ГМТ, которое в
некоторой декартовой системе координат
задается уравнением:
![]() (1)
(1)
где хотя бы один из коэффициентов а11, а12, а22 , отличен от нуля. Систему координат можно предполагать ОДСК, однако не сужая общности можно считать, что уравнение (1) задано в ПДСК. Теорема: общее уравнение линии второго порядка вида (1) задано относительно ПДСК. При помощи поворота осей координат и переноса можно привести к одному из следующих трех видов:
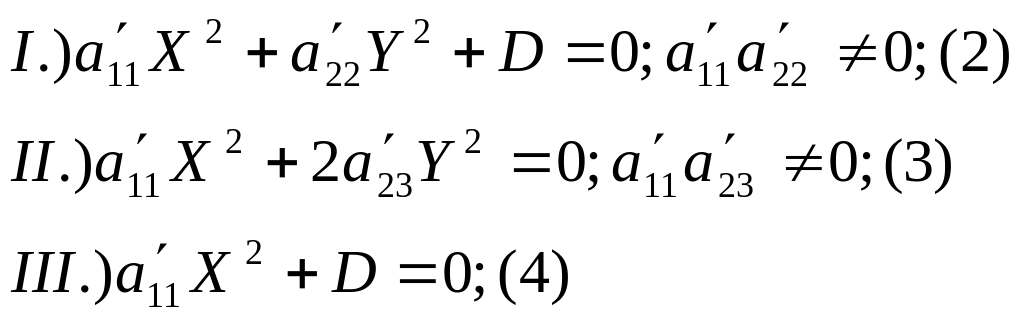 Уравнения
(2),(3),(4) называются простейшими уравнениями
линий второго порядка. Доказательство:
покажем, что можно от исходной ПДСК
перейти к новой ПДСК путем поворота
осей на угол α так, что в новой ПДСК будет
отсутствовать член с ху. Предположим,
что а12≠0,
тогда повернем ОХ и ОУ на некоторый угол
α, тогда координаты т. М(х,у) в системе
ХОУ через координаты (х`, у`) уже в новой
системе Х`ОУ` имеют вид:
Уравнения
(2),(3),(4) называются простейшими уравнениями
линий второго порядка. Доказательство:
покажем, что можно от исходной ПДСК
перейти к новой ПДСК путем поворота
осей на угол α так, что в новой ПДСК будет
отсутствовать член с ху. Предположим,
что а12≠0,
тогда повернем ОХ и ОУ на некоторый угол
α, тогда координаты т. М(х,у) в системе
ХОУ через координаты (х`, у`) уже в новой
системе Х`ОУ` имеют вид:
![]() (5)
(5)
Подставим (5) в уравнение (1), в итоге получим:
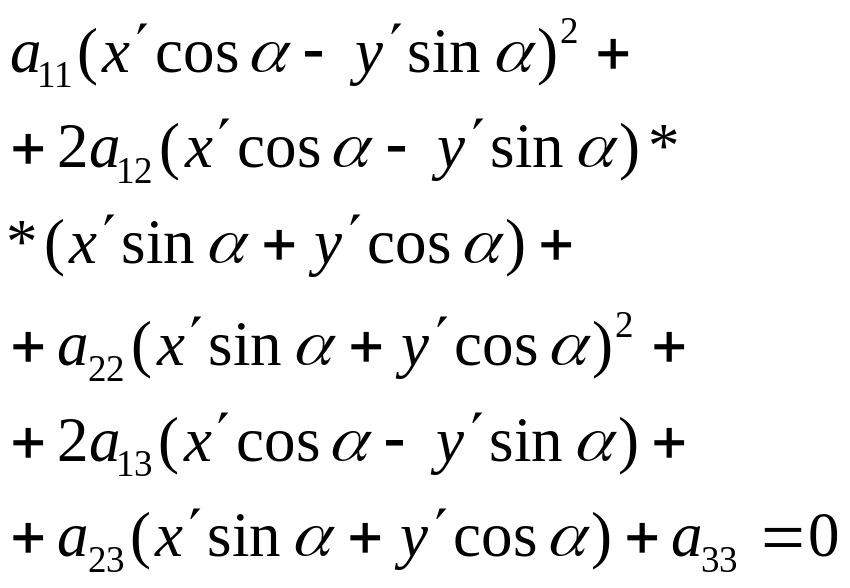
приведя подобные, выразив х`, у`, получим уравнение вида:
![]()
Где:
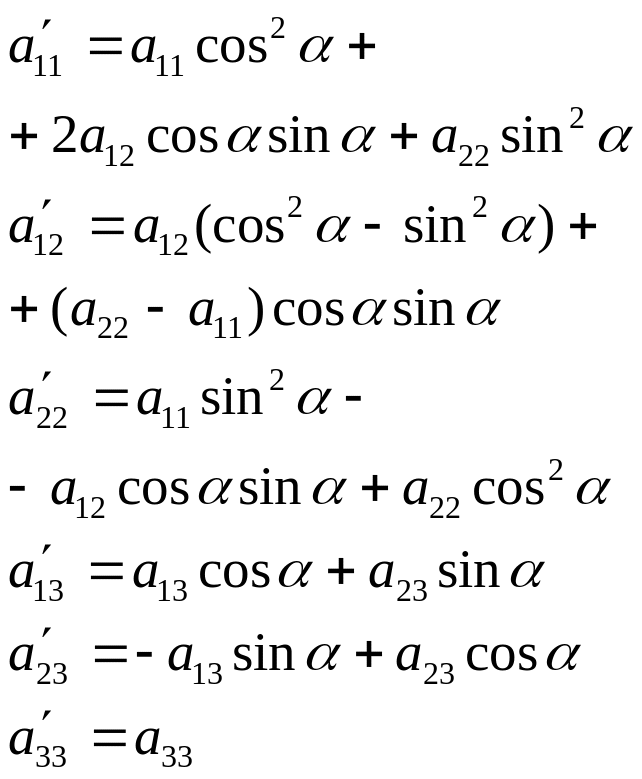
Поскольку
![]() должен быть равен нулю, то получаем
уравнение
должен быть равен нулю, то получаем
уравнение
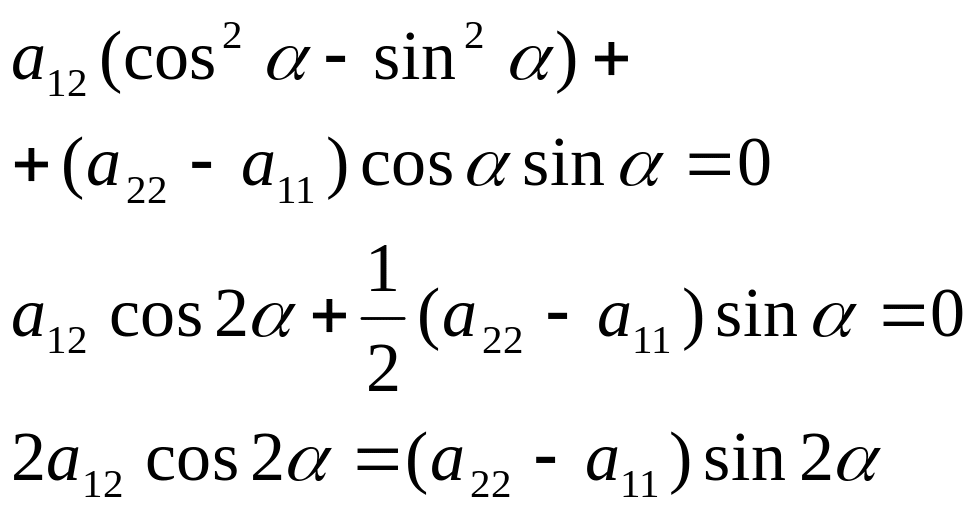 (7)
(7)
Поскольку:![]() (8)
(8)
Решая уравнение (8) находим угол α. Следовательно, при повороте плоскости ХОУ на полученый угол α в уравнении (6) будет отсутствовать член х`у`. таким образом, существует ПДСК, в которой уравнение вида (1) имеет вид (9):
1.) Если
![]() .
Выделим в уравнении (9) полные квадраты
возле
.
Выделим в уравнении (9) полные квадраты
возле
![]() и
и![]() .
Получим: (10)
.
Получим: (10)
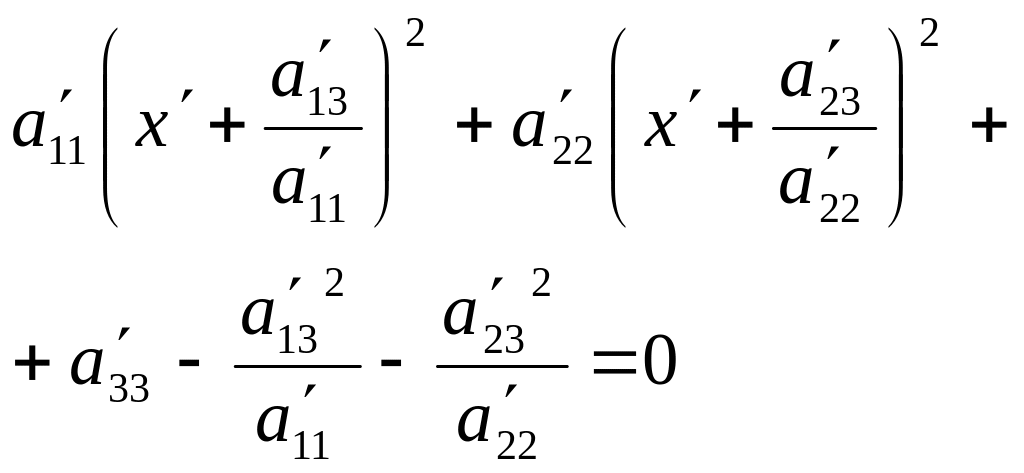
Произведем
параллельный перенос осей ОХ` и ОУ` так,
чтобы точка О перешла в О`. О`![]() тогда мы получим новую систему координат
ХО`У, где
тогда мы получим новую систему координат
ХО`У, где
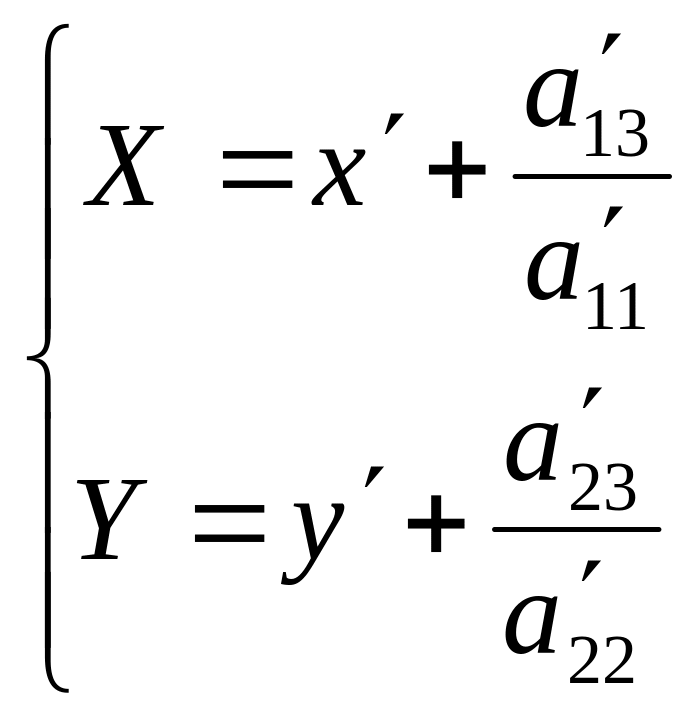
Тогда в новой
системе координат уравнение (9) имеет
вид
![]() , где
, где
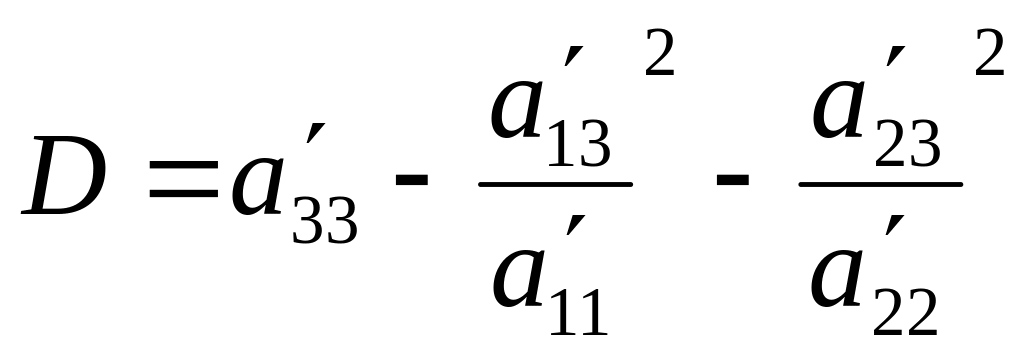 ,
то есть получим уравнение (2);
,
то есть получим уравнение (2);
2.)Если![]()
Пусть,
![]() тогда уравнение (9) имеет вид (11):
тогда уравнение (9) имеет вид (11):
![]()
Выделим полный
квадрат возле
![]() :
:
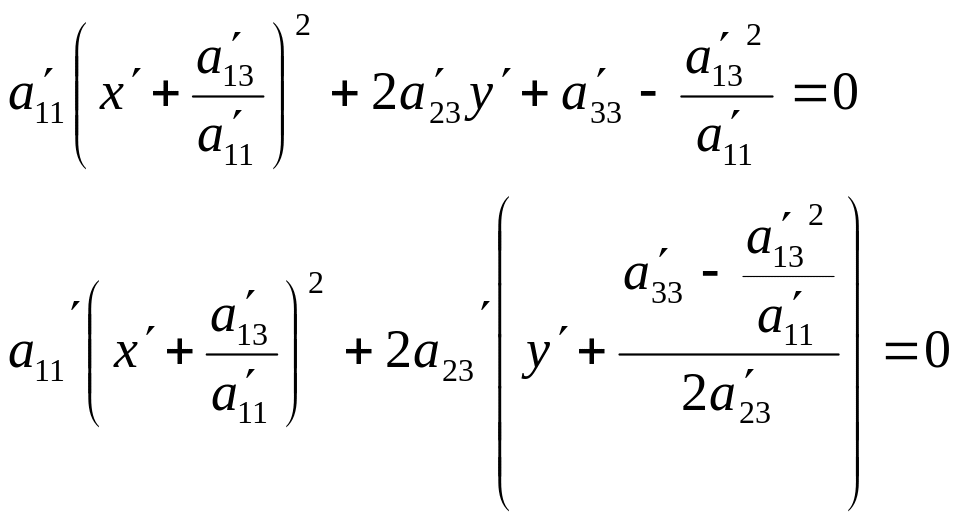
Произведем
параллельный перенос оси ОХ` и ОУ` так,
чтобы новым началом координат стала
точка О`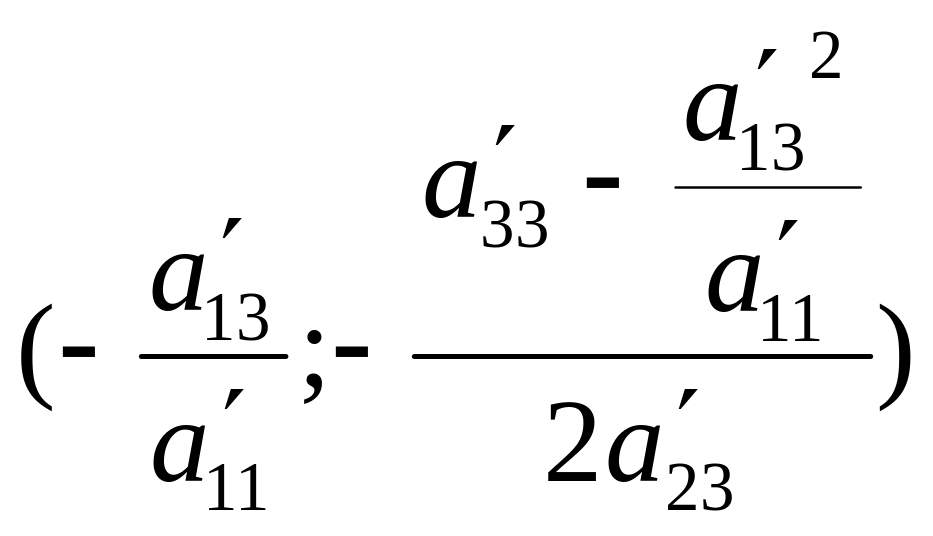
В результате получим
новую систему координат ХО`У, где
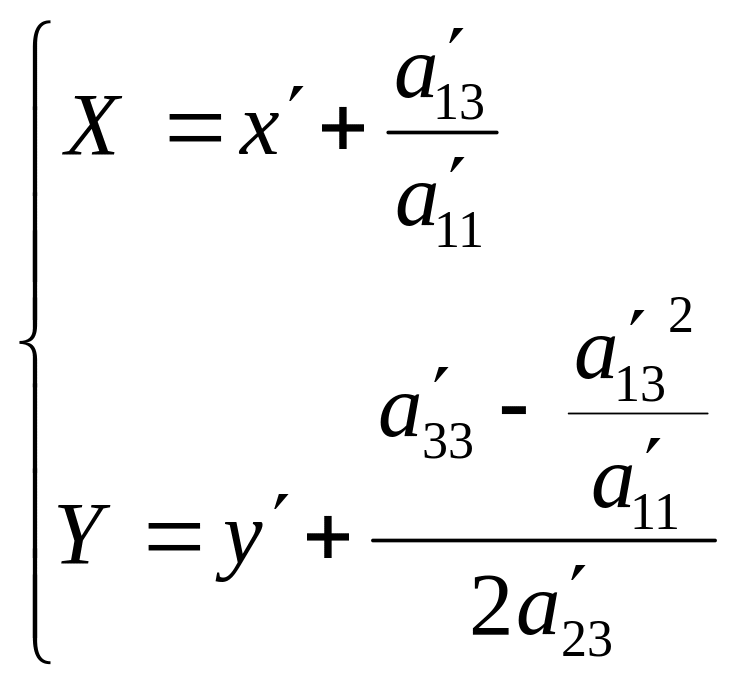
В результате
уравнение (1) примет вид
![]() ,
то есть уравнение, вида (3).
,
то есть уравнение, вида (3).
3.)Если![]() Пусть например
Пусть например
![]() .
Тогда уравнение (9) имеет вид
.
Тогда уравнение (9) имеет вид
![]() (12).
Выделяем полный квадрат
(12).
Выделяем полный квадрат
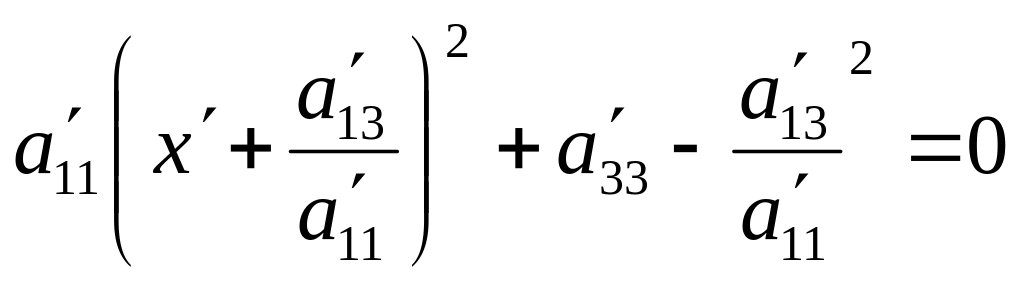 (13). Перенесем
оси координат так, что бы новым центром
О`(
(13). Перенесем
оси координат так, что бы новым центром
О`(![]() ;0).
Получим новую систему координат ХО`У,
где
;0).
Получим новую систему координат ХО`У,
где
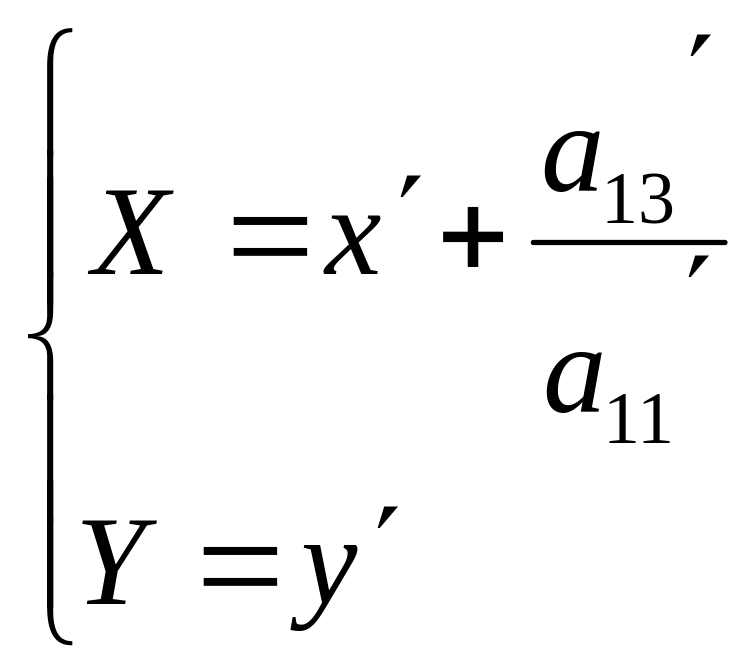
Тогда уравнение
(1) примет вид
![]() ,
то есть (4).
,
то есть (4).
§2. Линии, определяемые общим уравнением линий второго порядка.
Груп. |
№ |
Урав-ие |
Название |
І |
1
2
3
4
5 |
|
Эллипс
Мнимый эллипс
Две мн. пере- сек. прям.
Гипербола
Две пересек. прямые |
ІІ |
6 |
|
Парабола |
ІІI |
7
8
9 |
|
2 паралл. пр.
2 мн. парал. пр.
Две совп. пр. |
Доказательство:
Перейдем от ОДСК к ПДСК при этом очевидно порядок линий не меняется, и следовательно, уравнение будет иметь тот же вид. Уравнение (1) задано в ПДСК. Общее уравнение вида (1) может быть приведено к одному из следующих видов:
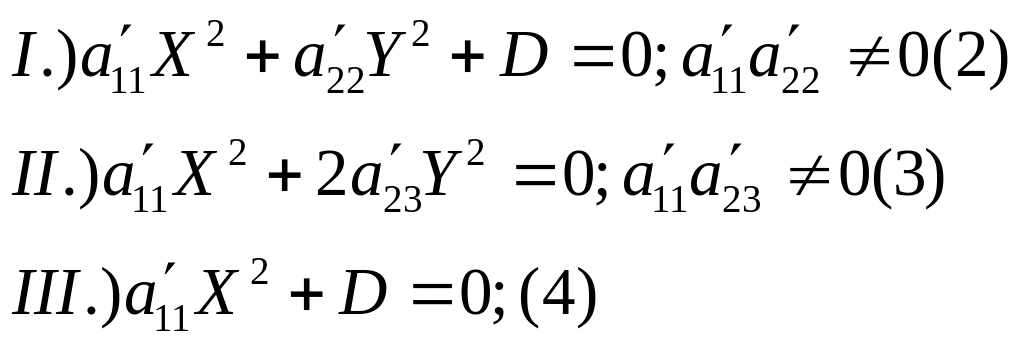
Пусть имеем уравнение вида (2):
І.
1.)
![]() и
D
имеет противоположный им знак
и
D
имеет противоположный им знак
![]() ,
,
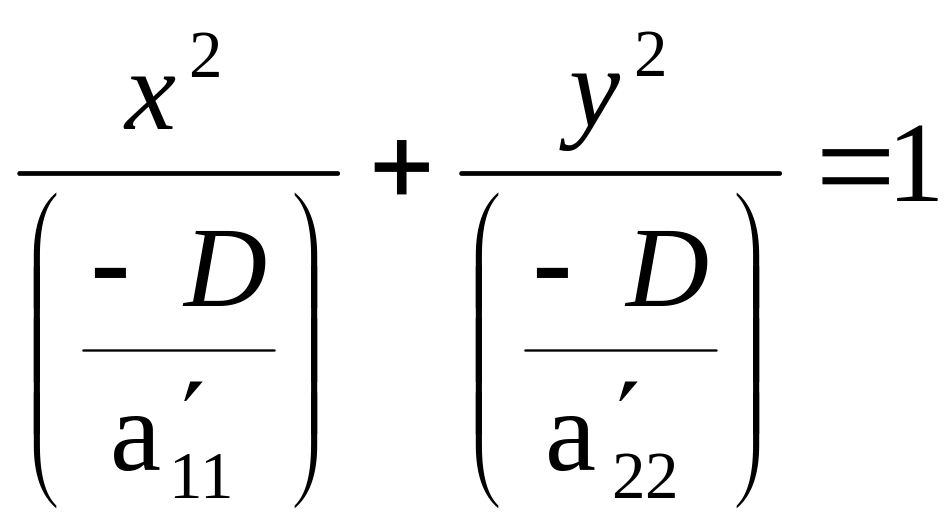
Обозначим через
![]() Получаем
Получаем
![]() →эллипс.
→эллипс.
2.)
![]() ,
D
– одного знака
,
D
– одного знака
![]() ,
,
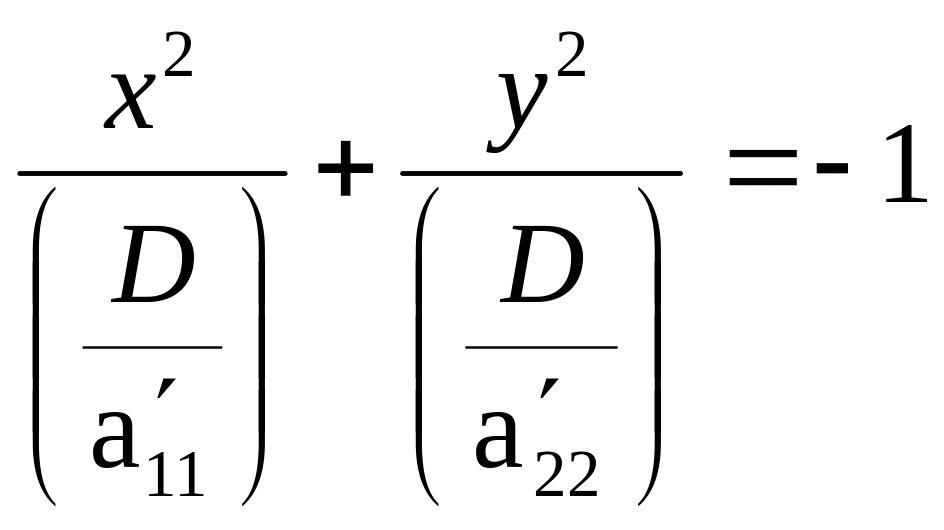 .
.
Обозначим:
![]()
получим
![]()
→мнимый эллипс.
3.)![]() ,
,
![]() ,
,
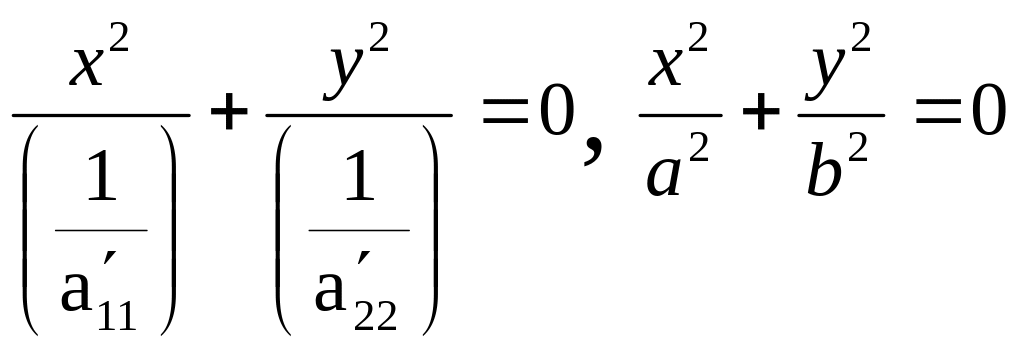
→2 мнимые пересекающиеся прямые.
4.)![]() ,
,
![]() ,
,
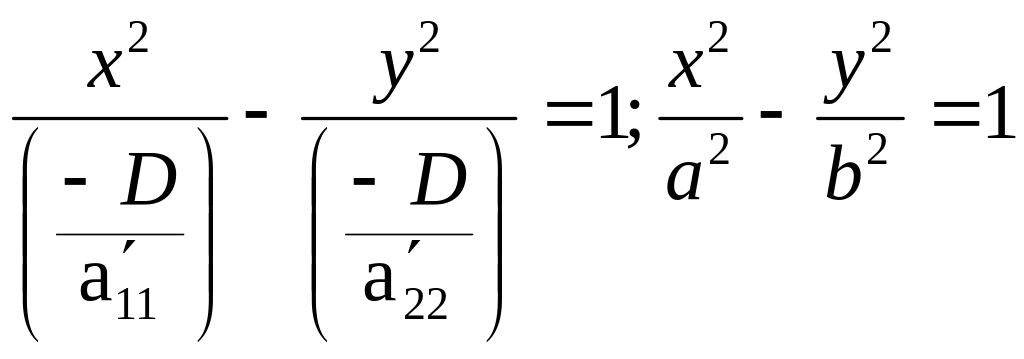
→гипербола.
5.)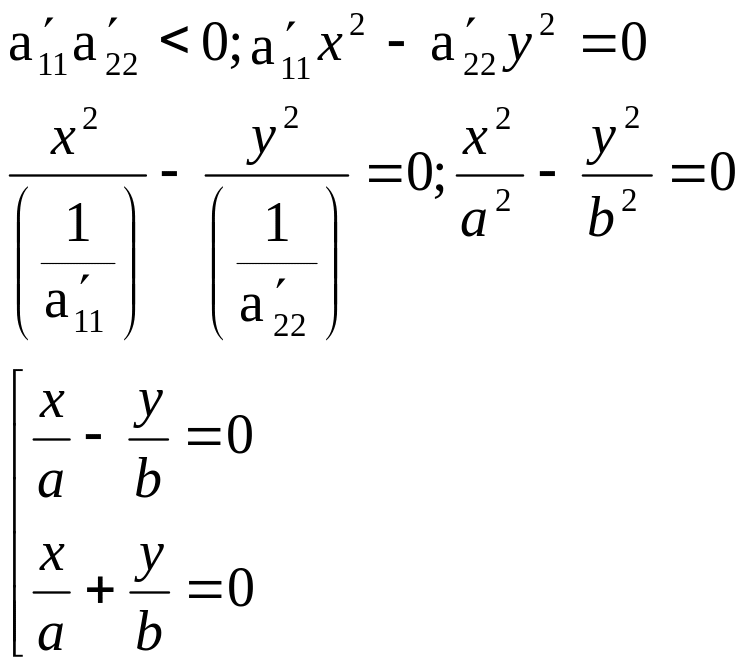
→2 пересекающиеся прямые.
ІІ.
6.)
Обозначив через
![]() получим
получим
![]() →парабола.
→парабола.
ІІІ.
7.)
Уравнение вида (4) можно привести к
![]() ,
получим
,
получим
![]() →2
параллельные прямые.
→2
параллельные прямые.
8.)
![]() ,
получаем х2
= - а2
,
получаем х2
= - а2
→2 мнимые параллельные прямые.
9.) D=0, получаем х2 =0 →2 совпадающие прямые.
