21. Первісна та невизначений інтеграл. Таблиця інтегралів.
Функція
зветься первісною функції
на деякому інтервалі дійсних чисел,
якщо
—
похідна функції
на цьому інтервалі, тобто в усіх внутрішніх
точках інтервалу виконується рівність
Можна довести, що у будь-якої неперервної на інтервалі функції існує первісна, яка також є неперервною функцією на цьому інтервалі.
Якщо
— будь-яка первісна функція
то
,
де C
- довільна стала, — також первісна цієї
функції і "невизначений інтеграл
функції
" посилається до множини
яка складається з усіх первісних функції
де С— довільна константа.
Із означення невизначеного інтеграла випливають такі властивості інтегрування:
1)
;
2)
;
3)
(метод заміни змінних, метод підстановки);
4)
(інтегрування частинами).
Наведемо таблицю основних інтегралів. Доведення кожної рівності полягає у її диференціюванні.
(n-1)
, у тому числі
;
;
;
;
,
у тому числі
;
;
;
;
;
,
у тому числі
;
,
у тому числі
;
.
22. Основні методи інтегрування
Основні методи інтегрування: безпосереднє інтегрування, інтегрування методом заміни змінної , інтегрування частинами.
Метод табличної (безпосередньої) інтеграції полягає в тому, що за допомогою еквівалентних перетворень функції і на підставі властивостей невизначеного інтеграла задані інтеграли перетворяться до табличних. Це дає можливість безпосередньо записати первісну.
Приклад
При безпосередній інтеграції часто застосовується прийом підведення функції під знак диференціала.
У підинтегральному виразі потрібно відшукати функцію, яку приймаємо за f׳(x) і підводимо під знак диференціала .
Інтеграція підстановкою
Метод полягає в перетворенні аргументу підінтегральної функції по деякій формулі, розрахованій на те, щоб інтеграл з новою змінною виявився простішим для обчислення. Після обчислення інтеграла з новою змінною потрібно повернутися до первинної змінної інтеграції.
Приклад
Знайти інтеграл
Застосуємо підстановку x = 2sint, тоді dx = 2costdt
Інтеграл з новою змінною виявляється табличним:
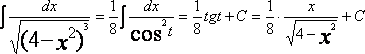
Інтеграція по частинах.
Формула методу інтеграції по частинах має вигляд:
Тут U, V – дві функції аргументу х, що диференціюються.
Метод інтеграції по частинах полягає в наступному.
Підінтегральну функцію початкового інтеграла розглядаємо як добуток функції U і диференціала деякої функції dV. За диференціал dV ми повинні вибрати вираз, для якого зможемо знайти первісну.
Після цього застосовуємо формулу методу інтеграції по частинах. Застосовувати формулу має сенс у тому випадку, коли інтеграл виявиться простішим початкового або подібний до нього. Для отримання остаточного результату іноді потрібно застосувати метод послідовно кілька разів.
Приклад
Покладемо
U = x, dV = cosxdx. Тоді dU = dx
23. Визначений інтеграл. Формула Ньютона-Лейбніца.
Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний смисл цього визначеного інтеграла — це площа криволінійної фігури, обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
Якщо у функції існує первісна , то
Ця формула називається формулою Ньютона-Лейбніца, або основною формулою інтегрального числення. Вона дає практичний і зручний спосіб обчислення визначеного інтеграла за значеннями первісної на кінцях відрізку інтегрування.