14. Похідна функції, таблиця похідних, диференціал.

Похідною функції y=f(x) в точці х називається границя відно­шення приросту функції до приросту аргументу, коли приріст аргу­менту прямує до нуля.

Похідна може позначатись f’(x), y’,

Правила диференціювання:

Нехай функції u=f(x) i v=g(x) мають у певній точці х₀ похідні u’, v’

1. Похідна від суми (різниці) двох функцій: (u ±v)’= u’ ±v’

2. Похідна від добутку двох функцій: (uv)' = u’v + uv’

3. Похідна від частки двох функцій: ,

4. Похідна складної функції: якщо y=f(u), u=g(x), то y’=f’(u)u’

Таблиця похідних:

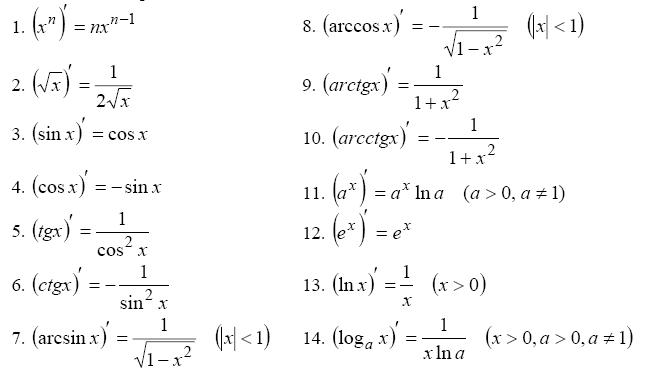
Якщо функція y=f(x) диференційована в точці х, тобто має в цій

точці скінченну похідну y’, то де при Звідси .

Головна частина приросту функції , лінійна відносно , нази­вається диференціалом функції і позначається dy :

dy=y’ або dy=y’

Справедлива формула або яка застосовується в наближених обчисленнях.

15. Наближені обчислення за допомогою диференціала. Похідні та диференціали вищих порядків.

Якщо функція y=f(x) диференційована в точці х, тобто має в цій

точці скінченну похідну y’, то де при Звідси .

Головна частина приросту функції , лінійна відносно , нази­вається диференціалом функції і позначається dy :

dy=y’ або dy=y’

Справедлива формула або яка застосовується в наближених обчисленнях.

Нехай функція y=f(x) визначена та має похідну першого порядку на інтервалі (a,b). Тоді її похідна y’=f’(x) також буде функцією, що визначена на інтервалі (a,b).Якщо ця функція сама є диференційованою в деякій точці х інтервалу (a,b), тобто має в цій точці похідну, то вказана похідна називається другою похідною або похідною 2-го порядку і позначається

y’’=(y’)’=f’’(x) або .

Аналогічно можна ввести поняття третьої похідної, потім четвертої і т.д.

Похідною n-го порядку називається похідна від похідної (n-1)-го порядку і позначається

Для похідних n-го порядку справедливі правила:

1. (u+v)⁽ⁿ⁾=u⁽ⁿ⁾+v⁽ⁿ⁾.

2.

Остання формула носить назву формули Лейбніця.

Якщо у' є диференційованою функцією, то можна визначити ди­ференціал другого порядку. Другим диференціалом (або диферен­ціалом другого порядку) називається диференціал від диференціала функції, тобто

d(dy)=d(y’dx)=d’’dx²=d²y або d²y=y’’dx²

Диференціалом n-го порядку називається перший диференціал від диференціала (n-1)-го порядку

dⁿy=d(d^n-1y)=y⁽ⁿ⁾dxⁿ

16. До основних теорем диференціального числення належать теорема Ролля, Лагранжа, Коші, Лопіталя та Ферма.

Правило Лопіталя для розкриття невизначеностей типу і полягає в такому : якщо функції f(x) і g(x) нескінченно малі або нескінченно великі при х →а, диференційовані в околі точки х=а, g(x)≠0 в околі цієї точки, існує , то існує і справедлива рівність

17. Точка x₀ називається точкою локального максимуму (мінімуму) функції y= f(x), якщо f(x₀) є найбільшим (найменшим) значенням функції в деякому околі цієї точки. Точки локального максимуму і мінімуму функції називаються точками екстремуму цієї функції.

Необхідна ознака існування екстремуму : якщо неперервна функція f(x) має в точці x= x₀ екстремум, то похідна функції f′(x)=0 або не існує. Точки, в яких похідна дорівнює нулю або не існує, називаються критичними (стаціонарними, підозрілими на екстремум)

Достатня ознака існування екстремуму функції за першою похідною. Якщо при переході через критичну точку x₀ похідна диференційованої функції y= f(x) змінює свій знак з плюса на мінус, то точка x₀ – це точка екстремуму, а якщо з мінуса на плюс, то точка мінімуму.

Достатня ознака існування екстремуму функції за другою похідною. Якщо функція f(x) має в критичній точці x₀ скінченну другу похідну, то вона має в точці x₀ локальний максимум, якщо f′′(x)<0, і локальний мінімум, якщо f′′(x)>0.

Якщо функція f(x) неперервна на відрізку [a,b], то вона досягає на цьому відрізку своїх найбільшого та найменшого значень. Для знаходження цих значень необхідно знайти всі критичні точки на [a,b], обчислити значення f(x) в цих точках і в точках х=а, х=b та серед знайдених значень вибрати найбільше і найменше.

Загальна схема дослідження функції та побудови графіка:

Знайти область визначення функції

Дослідити ф-ю на парність/непарність, періодичність

Знайти вертикальні асимптоти

Дослідити поведінку функції на нескінченності, знайти горизонтальні та похилі асимптоти

Знайти екстремуми та інтервали монотонності ф-ї

Знайти інтервал опуклості ф-ї та точки перегину

Знайти точки перегину з осями координат

Побудувати асимптоти, точки перегину з осями, екстремальні точки, точки перегину та графік.

18. Частинною похідною від функції z=f(x,y) за незалежною змінною х називається скінченна границя

= = f′_x(x,y)

обчислена при постійному y.

Частинною похідною від функції z=f(x,y) за незалежною змінною y називається скінченна границя

= = f′_y(x,y) , обчислена при постійному х.

Для частинних похідних справедливі звичайні правила та формули диференціювання.

Частинними похідними другого порядку від функції z=f(x,y) називаються частинні похідні від її частинних похідних першого порядку

z′′_xx= = ( )

z′′_xy= = ( )

z′′_yx= = ( )

z′′_yy= = ( )

19. Диференціал функції багатьох змінних

20. Екстремум функції багатьох змінних

Означення 1.2. Значення функції z у точці екстремуму (максимуму або мінімуму) називається локальним екстремумом (максимумом або мінімумом) цієї функції.

Функція декількох змінних, зрештою, як і функція однієї змінної, може мати декілька або безліч локальних екстремумів, а може не мати жодного.