2.2.Кратчайшие пути от фиксированной вершины

Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опирается на действия, которые в общих чертах можно представить следующим образом: при данной матрице весов дуг , вычисляет некоторые верхние ограничения D[v] на расстояния от s до всех вершин . Каждый раз, когда устанавливается, что

D[u] + A[u,v] < D[v] (2.1)

оценку D[v] улучшают: D[v] = D[u] + A[u,v].

Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно. Легко показать, что значение каждой из переменных D[v] равно тогда d(s,v) – расстоянию от s до v. Для определения расстояния от s до t вычисляются расстояния от s до всех вершин графа. Не известен ни один алгоритм нахождения расстояния между двумя фиксированными вершинами, который был бы существенным образом более эффективен, нежели известные алгоритмы определения расстояния от фиксированной вершины до всех остальных.

Описанная общая схема является неполной, так как она не определяет очередности, в которой выбираются вершины u и v для проверки условия (2.1). Эта очередность оказывает сильное влияние на эффективность алгоритма. Рассмотрим более детально методы нахождения расстояния от фиксированной вершины, называемой источником, всегда обозначаемого через s, до всех остальных вершин графа.

Рассмотрим сначала алгоритм для общего случая, в котором предполагается только отсутствие контуров с отрицательной длиной. Ориентированный граф G в своих кольцевых структурах так же как в 2.1 содержит номера вершин (n) и веса дуг (a). В отличие от 2.1 номера вершин связаны не с приходящими дугами, а с выходящими.

Алгоритм 2.2 = proc (G:graph; s:int) returns (D:array of int) effects 1. для i = 1 до n D[i] = ; D[s] = 0 2. c = graph.fetch(G,s); i = circ.size(c) 3. пока i > 0 3.1. D[circ.element(c).n] = circ.element(c).a 3.2. circ.change(c); i = i – 1 4. для k = 1 до n-2 4.1. для v = 1 до n 4.1.1. если v < > s, то 4.1.1.1. для u = 1 до n 4.1.1.1.1. c = graph.fetch(G,u) 4.1.1.1.2. для i = 1 до circ.size(c) если (circ.element(c).n < > v), то circ.change(c) иначе 4.1.1.1.2.1. a = circ.element(c).a + D[u] 4.1.1.1.2.2. если (a < D[v]), то D[v] = a

Рис.2.2.Процедура нахождения расстояния от источника до всех вершин ориентированного графа – метод Форда-Беллмана.

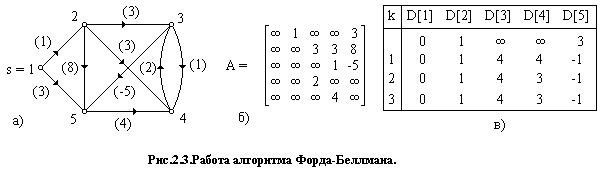Работа алгоритма Форда-Беллмана проиллюстрирована на рис.2.3, веса дуг даны числами в скобках.

2.3.Случай неотрицательных весов – алгоритм Дейкстры

Известны более эффективные алгоритмы для двух важных случаев, таких как: веса всех дуг неотрицательны или граф бесконтурен. Первый случай решается с помощью алгоритма Дейкстры. Веса дуг содержатся в массиве A[n, n]. Дополнительно введен массив B[n] признаков вхождения (1) или исключения (0) вершины из множества вершин графа. В исходном состоянии B[i] = 1 для всех вершин.

Алгоритм 2.3 = proc (A,B:array of int; s:int) returns (D:array of int) effects 1. для i = 1 до n D[i] =A[s, i]; D[s] = 0; B[s] = 0; k = n –1; 2. пока k > 0 2.1. b = 2.2. для i = 1 до n если ((B[i] = 1) и (D[i] < b)), то 2.2.1. b = D[i] 2.2.2. u = i 2.3. B[u] = 0; k = k – 1 2.4. для i = 1 до n если (B[i] = 1), то D[i] = min(D[i], D[u] + A[u, i])

Р ис.2.4.Алгоритм нахождения расстояния от источника до всех остальных вершин в графе с неотрицательными весами дуг – метод Дейкстры.

Работа алгоритма Дейкстры проиллюстрирована на рис.2.5 ( V = {1,2, . . . ,6}, веса дуг даны в скобках, значения , обозначены кружками, минимальные значения – двойными кружками).