
- •Составители: доц. Валерий Леонидович Шур
- •§1. Числовые ряды
- •§2. Признаки сходимости числовых рядов
- •§3. Знакопеременные ряды
- •§4. Степенные ряды
- •§5. Применение степенных рядов к вычислению определенных интегралов и к решению дифференциальных уравнений
- •§6. Ряды Фурье
- •Индивидуальные домашние задания
- •Библиографический список
§5. Применение степенных рядов к вычислению определенных интегралов и к решению дифференциальных уравнений
Рядом Тейлора
функции
относительно точки
![]() называется степенной ряд вида
называется степенной ряд вида
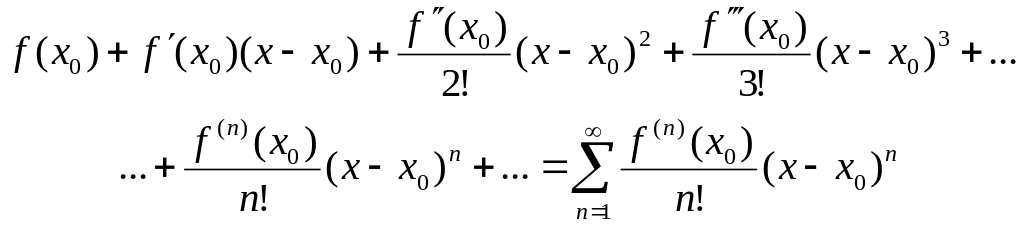
Коэффициенты этого ряда
![]()
называются коэффициентами Тейлора функции .
Укажем
алгоритм разложения функции
в ряд Тейлора
по степеням
![]() .
.
1) Записать общий вид ряда Тейлора.
2) Найти производные
![]() .
Установить закономерность для
.
Установить закономерность для
![]() .
.
3) Вычислить значение
функции и значения производных для
![]() .
Установить закономерность.
.
Установить закономерность.
4) Подставить найденные значения в ряд Тейлора.
5) Найти область сходимости ряда Тейлора.
6) Записать разложение в ряд с указанием области сходимости.
Пример 5.1.
Разложить в ряд Тейлора по степеням
![]() функцию
функцию
![]() .
.
Решение.
1) Записываем ряд
Тейлора,
![]() :
:
![]()
![]() .
.
2) Находим производные:
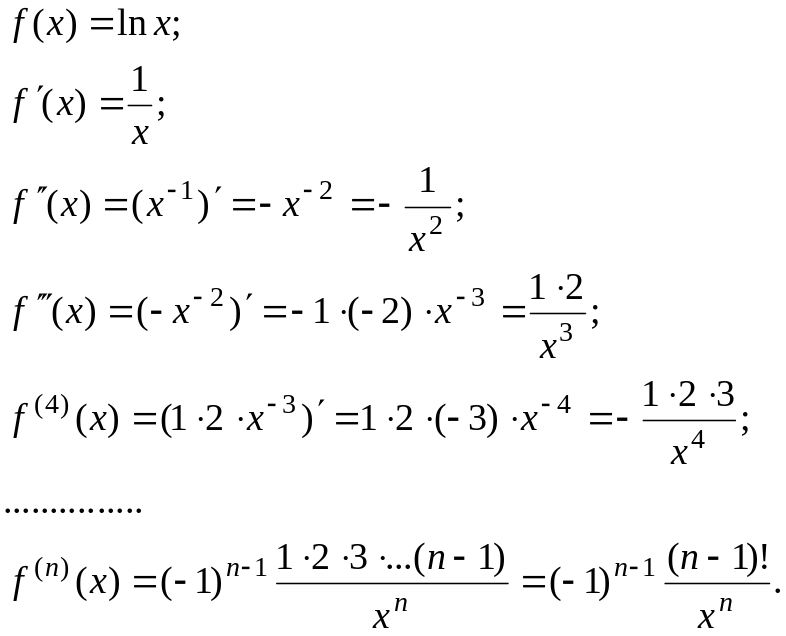
3) Вычисляем значение
функции и значения производных при
![]() :
:
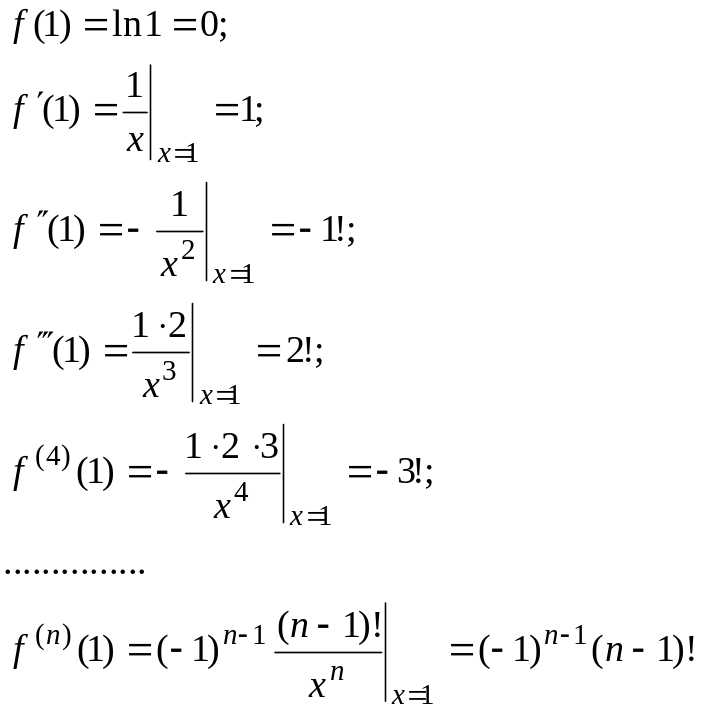
4) Подставляем найденные значения в ряд Тейлора:
![]()
![]() (1)
(1)
5) Находим область сходимости ряда Тейлора (1):
![]() ,
Следовательно, интервал сходимости
,
Следовательно, интервал сходимости
![]() .
.
Исследуем ряд на
концах интервала. При
![]() ряд (1) имеет вид
ряд (1) имеет вид
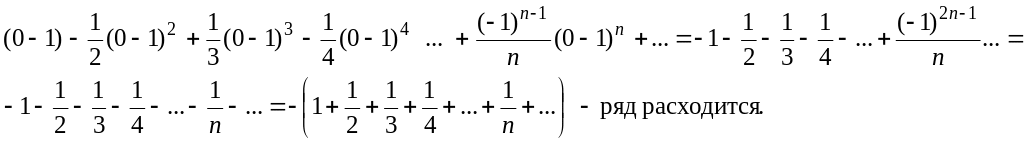 При
При
![]() ряд (1) имеет вид
ряд (1) имеет вид
![]()
Это знакочередующийся
ряд и, применяя признак Лейбница, получаем
![]() ,
то есть он сходится. Так как ряд,
составленный из абсолютных величин
,
то есть он сходится. Так как ряд,
составленный из абсолютных величин
![]() расходится, то при
ряд (1) сходится условно.
расходится, то при
ряд (1) сходится условно.
Область сходимости
ряда (1)
![]() .
.
6) Записываем
разложение функции
![]() по степеням
с указанием области сходимости:
по степеням
с указанием области сходимости:
![]()
Ряд Тейлора
![]() ,
при
,
называют рядом
Маклорена.
,
при
,
называют рядом
Маклорена.
Приведем разложения в ряд Маклорена для некоторых элементарных функций:
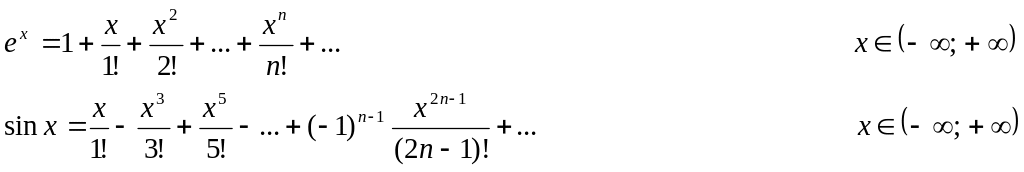
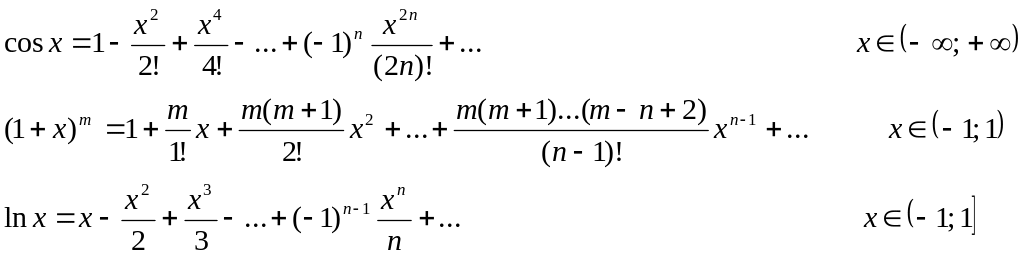
Степенной ряд можно почленно интегрировать и дифференцировать в любой точке его интервала сходимости.
Пример 5.2.
Вычислить определенный интеграл
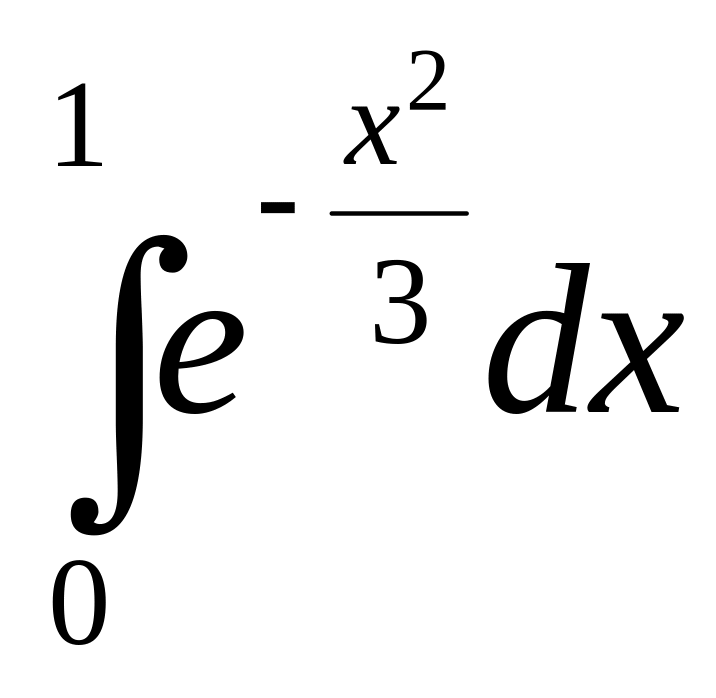 с точностью до 0,001.
с точностью до 0,001.
Решение. Разложим подынтегральную функцию в ряд. Имеем
![]()
Заменяя t
на
![]() получим
получим
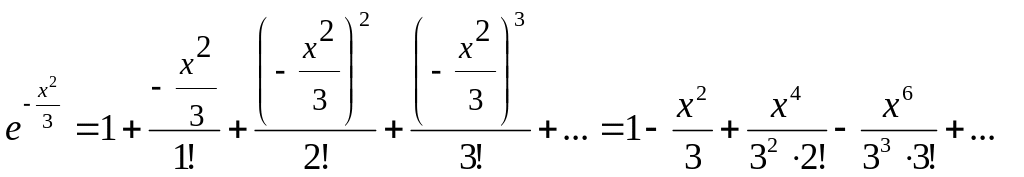 .
.
Подставляя разложение подынтегральной функции в интеграл, получаем:
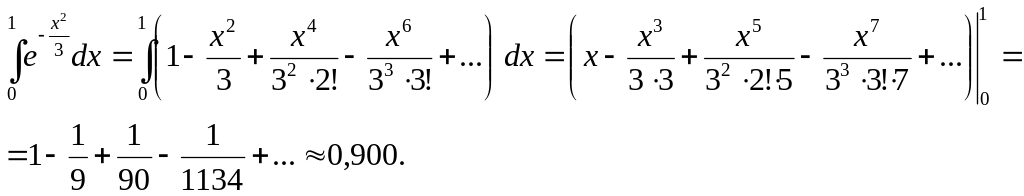
Можно ограничиться первыми тремя членами ряда, так как четвертый член знакочередующегося ряда меньше 0,001, поэтому сумма ряда, начинающегося с четвертого члена, будет меньше 0,001 и, в рамках заданной точности, весь этот ряд можно отбросить.
Пример 5.3.
Найти три первых отличных от нуля члена
разложения в степенной ряд решения
![]() дифференциального уравнения
дифференциального уравнения
![]() ,
удовлетворяющего начальному условию
,
удовлетворяющего начальному условию
![]() .
.
Решение. Для решения поставленной задачи воспользуемся методом последовательного дифференцирования. Будем искать решение с помощью ряда Маклорена.
![]() .
.
Из начального
условия
,
тогда
![]() .
Для нахождения следующего коэффициента
продифференцируем обе части уравнения
,
получим
.
Для нахождения следующего коэффициента
продифференцируем обе части уравнения
,
получим
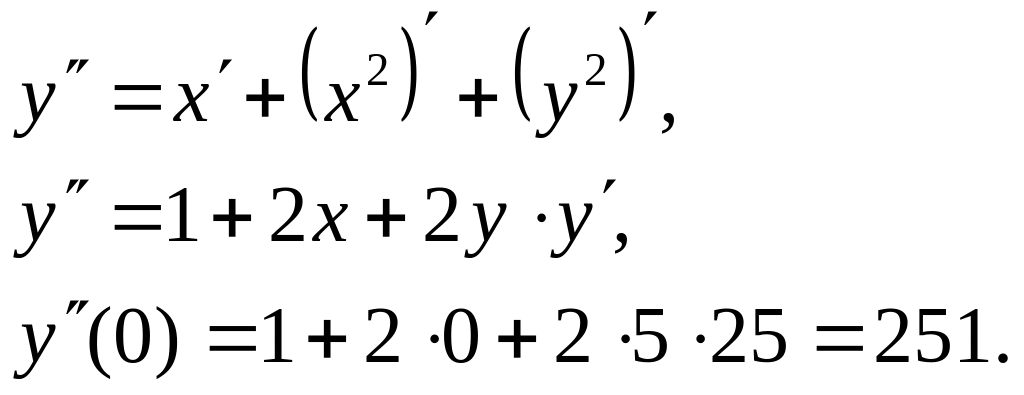
Решение дифференциального уравнения имеет вид
![]() .
.
Пример 5.4. Найти
решение дифференциального уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() .
.
Решение. Для решения задачи воспользуемся методом неопределенных коэффициентов. Разложим свободный коэффициент уравнения в степенной ряд
![]() .
.
Решение уравнения
будем искать в виде
![]() .
.
Тогда
![]()
Из начальных
условий находим:
![]() .
.
Для нахождения
следующих коэффициентов подставляем
полученные разложения для
![]() в дифференциальное уравнение
в дифференциальное уравнение
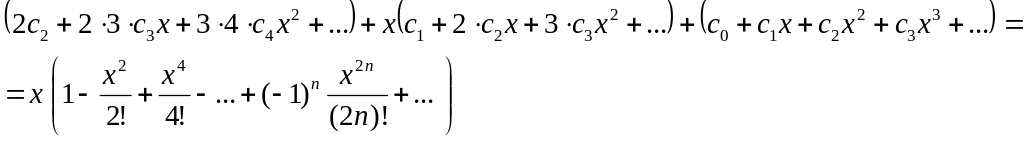
Приравняем
коэффициенты при одинаковых степенях
![]() :
:
|
|
|
|
|
|
|
|
|
|
Учитывая, что
находим, что
![]() ,
,
![]() . Таким образом, решение уравнения имеет
вид
. Таким образом, решение уравнения имеет
вид
![]() ,
,
то есть
![]() .
.
