Задание n 18 Тема: Элементы специальной теории относительности

Объем воды в Мировом океане равен 1,37·10⁹ км³. Если температура воды повысится на 1°С, увеличение массы воды составит _______ . (Плотность морской воды 1,03 г/см³, удельная теплоемкость 4,19 кДж/(кг·К).)

			6,57·107 кг
			65,7 т
			65,7 кг
			6,57·10-2 кг

Решение: Из закона взаимосвязи массы и энергии следует, что изменение энергии покоя сопровождается изменением массы тела, причем эти изменения пропорциональны друг другу:  , где  – скорость света в вакууме. Изменение температуры воды в Мировом океане означает, что вода получила количество теплоты, равное , где  – удельная теплоемкость воды,  – ее плотность,  – объем. Тогда увеличение массы воды составит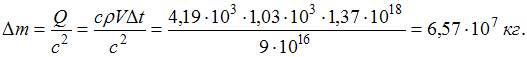 

Задание n 1 Тема: Свободные и вынужденные колебания

Пружинный маятник с жесткостью пружины  совершает вынужденные колебания со слабым коэффициентом затухания  которые подчиняются дифференциальному уравнению 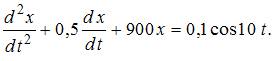 Амплитуда колебаний будет максимальна, если массу груза увеличить в _____ раз(-а).

9

Решение: Дифференциальное уравнение вынужденных колебаний имеет вид  , где  коэффициент затухания,  собственная круговая частота колебаний;  амплитудное значение вынуждающей силы, деленное на массу;  частота вынуждающей силы. При слабом затухании (коэффициент затухания значительно меньше собственной частоты колебаний маятника) амплитуда колебаний будет максимальна, если частота вынуждающей силы совпадет с собственной частотой колебаний маятника (явление резонанса). Собственная частота колебаний равна:  частота вынуждающей силы  . Для пружинного маятника 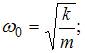 значит, масса груза 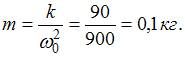 Чтобы частота вынуждающей силы совпала с собственной частотой колебаний маятника, масса должна быть равна 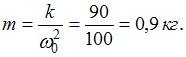 Следовательно, массу груза нужно увеличить в 9 раз.

Задание n 2 Тема: Сложение гармонических колебаний

Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными  и  . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний. 1.  2.  3. 

1
2
3

Решение: Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле  , где  и  – амплитуды складываемых колебаний, ( ) – разность их фаз. Если амплитуда результирующего колебания  , то  . Тогда  и разность фаз складываемых колебаний равна  . Если  , то  . Тогда  , следовательно,  . Если  , то  . Тогда  , следовательно,  .