
- •Екзаменаційний білет № 1
- •Екзаменаційний білет № 2
- •Національний технічний університет України „Київський політехнічний інститут”
- •Екзаменаційний білет № 3
- •Розв’язати інтегральне рівняння: .
- •Екзаменаційний білет № 4
- •Екзаменаційний білет № 5
- •Обчислити .
- •Екзаменаційний білет № 6
- •Обчислити .
- •Розв’язати інтегральне рівняння .
- •Екзаменаційний білет № 7
- •Обчислити .
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 8
- •Обчислити .
- •Національний технічний університет України „Київський політехнічний інститут”
- •Екзаменаційний білет № 9
- •Обчислити .
- •Екзаменаційний білет № 10
- •Обчислити .
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 11
- •Обчислити .
- •Розв’язати інтегральне рівняння: .
- •Екзаменаційний білет № 12
- •Обчислити , де .
- •Екзаменаційний білет № 13
- •Обчислити .
- •Розв’язати інтегральне рівняння: .
- •Екзаменаційний білет № 14
- •Обчислити .
- •Екзаменаційний білет № 15
- •Обчислити .
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 16
- •Обчислити .
- •Розв’язати інтегральне рівняння: .
- •Екзаменаційний білет № 17
- •Обчислити .
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 18
- •Обчислити .
- •Розв’язати інтегральне рівняння: .
- •Екзаменаційний білет № 19
- •Обчислити .
- •Екзаменаційний білет № 20
- •Обчислити .
- •Екзаменаційний білет № 21
- •Обчислити .
- •Екзаменаційний білет № 22
- •Обчислити .
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 23
- •Обчислити .
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 24
- •Обчислити .
- •Екзаменаційний білет № 25
- •Обчислити .
- •Екзаменаційний білет № 26
- •Обчислити .
- •Екзаменаційний білет № 27
- •Розв’язати задачу Коші: .
- •Екзаменаційний білет № 28
- •Обчислити .
- •Екзаменаційний білет № 29
- •Обчислити .
- •Екзаменаційний білет № 30
- •Обчислити
Національний технічний університет України „Київський політехнічний інститут”
(назва вищого навчального закладу)
Факультет ФМФ семестр 6
Навчальний предмет Теорія функцій комплексної змінної
Екзаменаційний білет № 1
Означення похідної функції комплексної змінної. Означення диференційованої (моногенної), аналітичної функції. Необхідна та достатня умова диференційованості: формулювання та доведення. Умова Коші-Рімана (Даламбера-Ейлера).
Означення лишку у нескінченно віддаленій точці. Обчислення таких лишків. Узагальнення основної теореми про лишки: формулювання та доведення.
Нехай
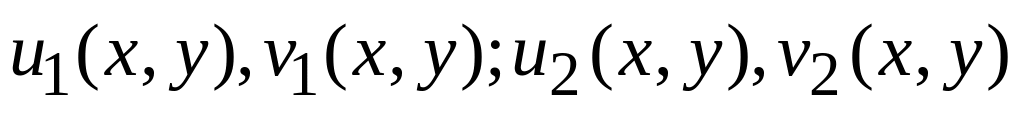 - дві пари спряжених гармонічних функцій
в області D, причому
- дві пари спряжених гармонічних функцій
в області D, причому
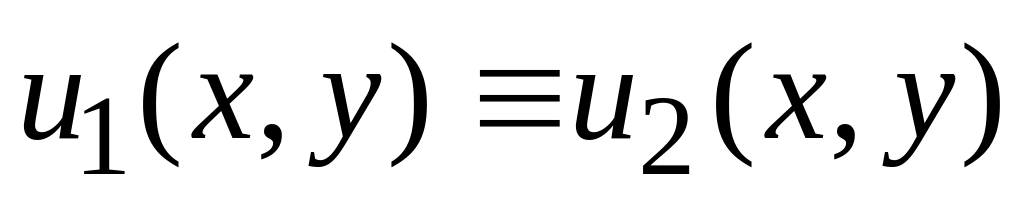 .
Довести, що
.
Довести, що
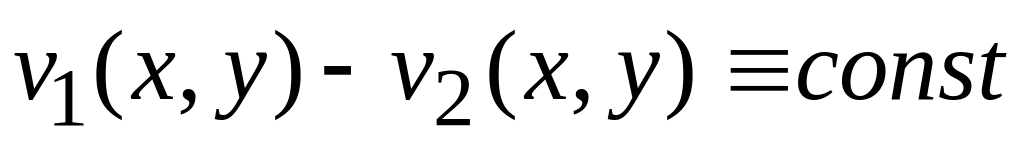 .
.Знайти особливі точки функції
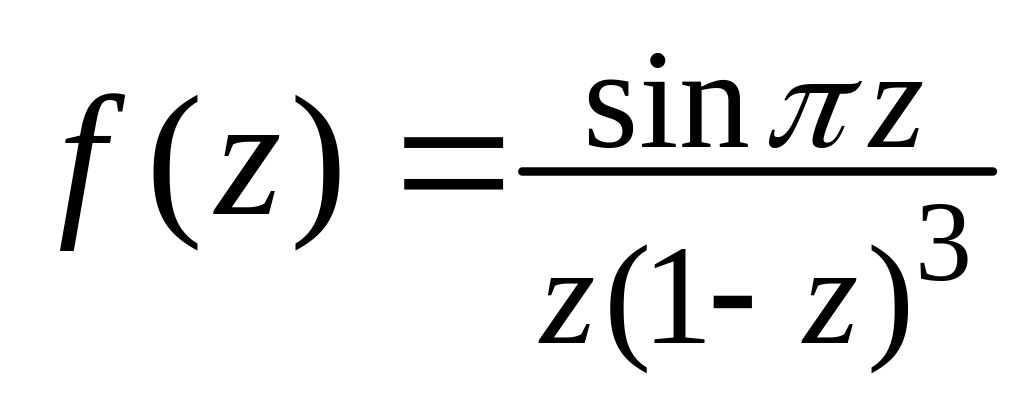 ,
встановити їх тип, обчислити лишки.
,
встановити їх тип, обчислити лишки.Розв’язати інтегральне рівняння
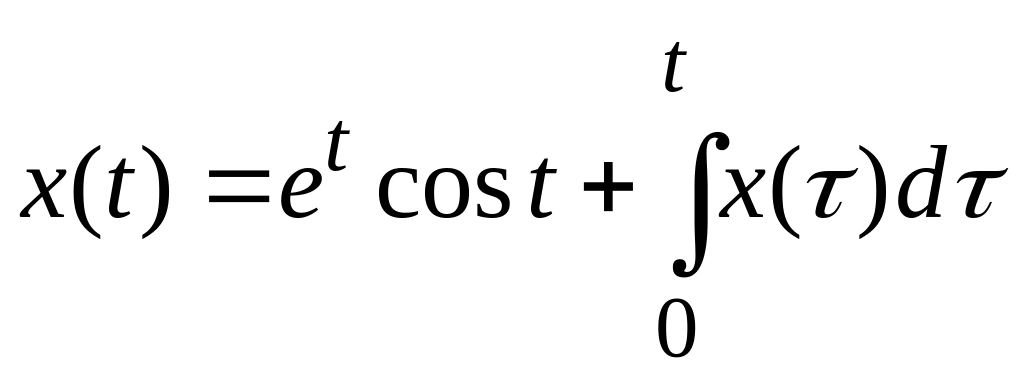 .
.
Затверджено на засіданні кафедри математичного аналізу та теорії ймовірностей
протокол № 10 від „14” травня 2008 р.
Зав. кафедри Булдигін В.В. Екзаменатор Горленко С.В.
Національний технічний університет України „Київський політехнічний інститут”
(назва вищого навчального закладу)
Факультет ФМФ семестр 6
Навчальний предмет Теорія функцій комплексної змінної
Екзаменаційний білет № 2
Геометричний зміст модуля та аргументу похідної функції комплексної змінної. Поняття про конформні відображення 1-го та 2-го роду, приклади.
Означення логарифмічного лишку функції відносно контуру. Теорема про зв’язок логарифмічного лишку функції з кількістю її нулів та полюсів в області: формулювання та доведення.
Функцію
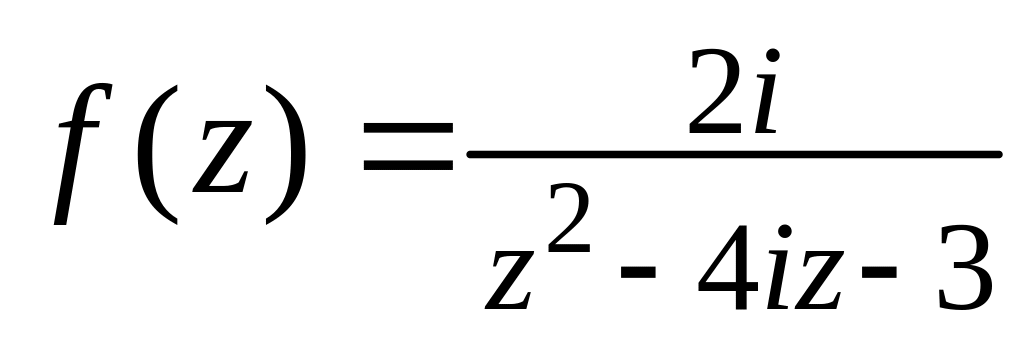 розвинути в ряд Лорана в околі особливої
точки
розвинути в ряд Лорана в околі особливої
точки
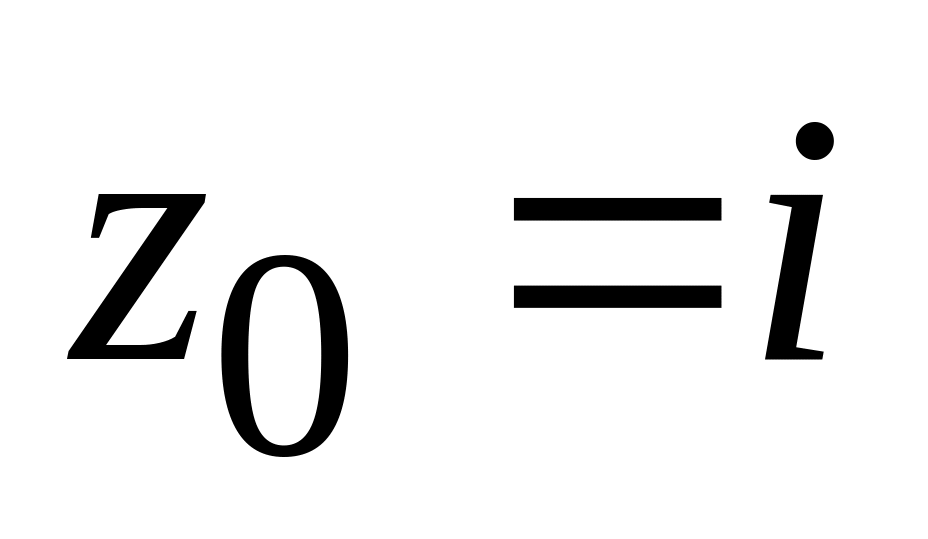 .
Вказати область збіжності отриманого
ряду та знайти
.
Вказати область збіжності отриманого
ряду та знайти
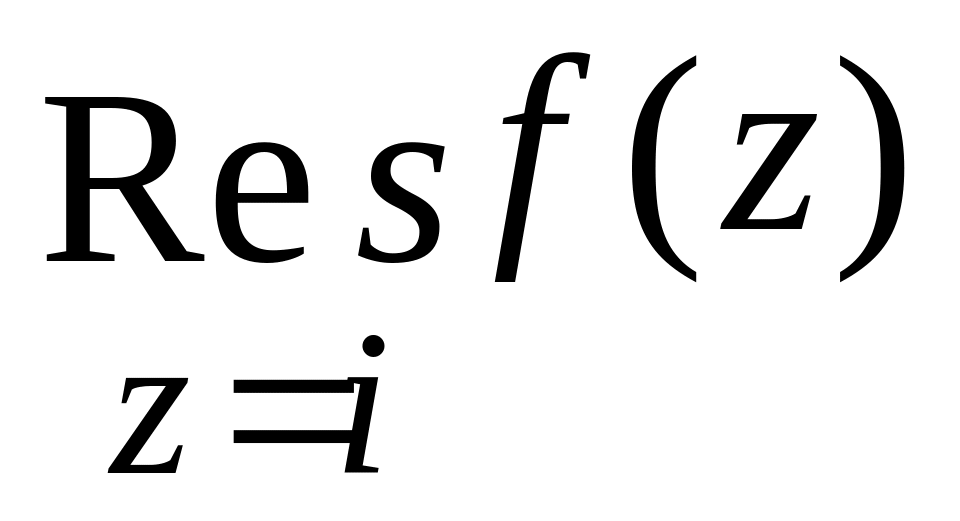 .
.Обчислити
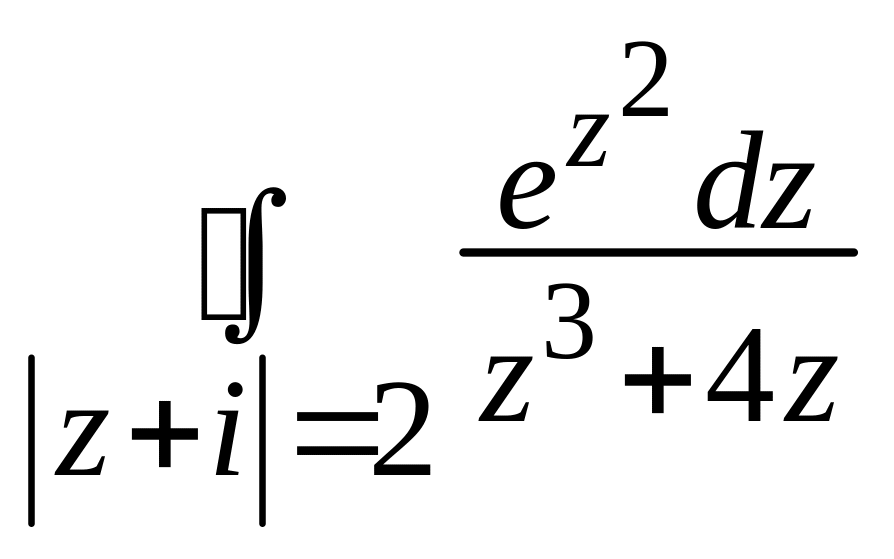 .
.Розв’язати задачу Коші:
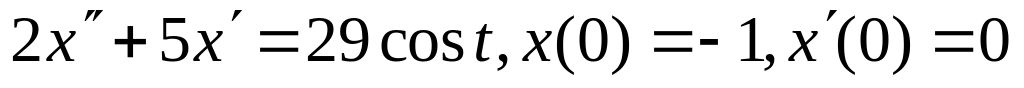 .
.
Затверджено на засіданні кафедри математичного аналізу та теорії ймовірностей
протокол № 10 від „14” травня 2008 р.
Зав. кафедри Булдигін В.В. Екзаменатор Горленко С.В.
Національний технічний університет України „Київський політехнічний інститут”
(назва вищого навчального закладу)
Факультет ФМФ семестр 6
Навчальний предмет Теорія функцій комплексної змінної
Екзаменаційний білет № 3
Дробово-лінійна функція комплексної змінної: означення та доведення кругової властивості.
Принцип аргументу: формулювання та доведення. Знаходження кількості нулів аналітичної в області функції.
Обчислити
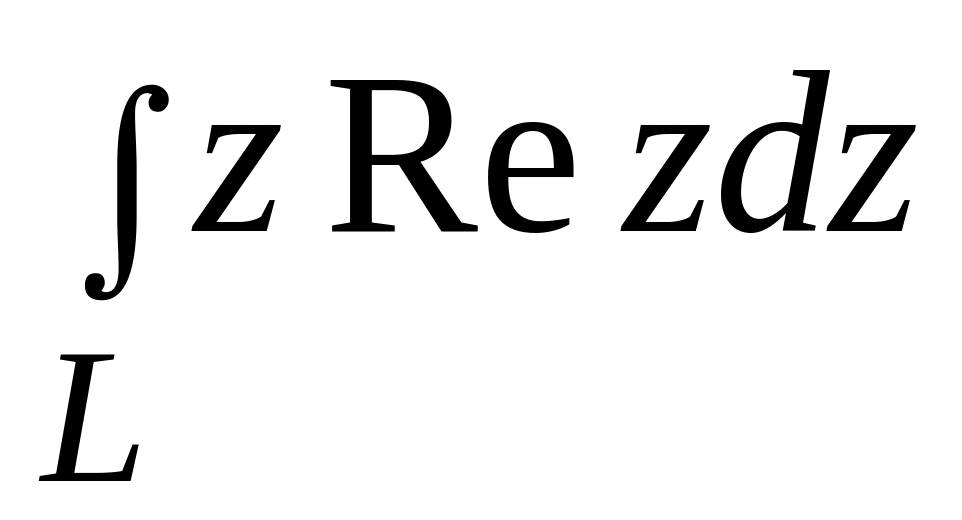 ,
де
,
де
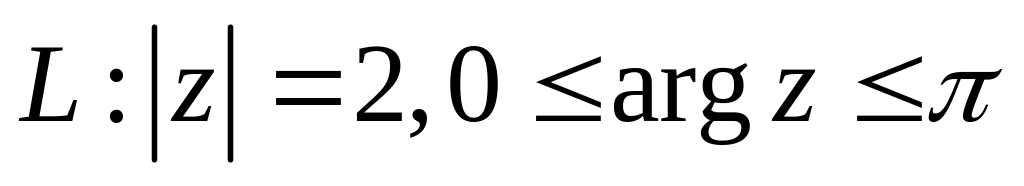 .
.Знайти всі можливі виду розвинення функції
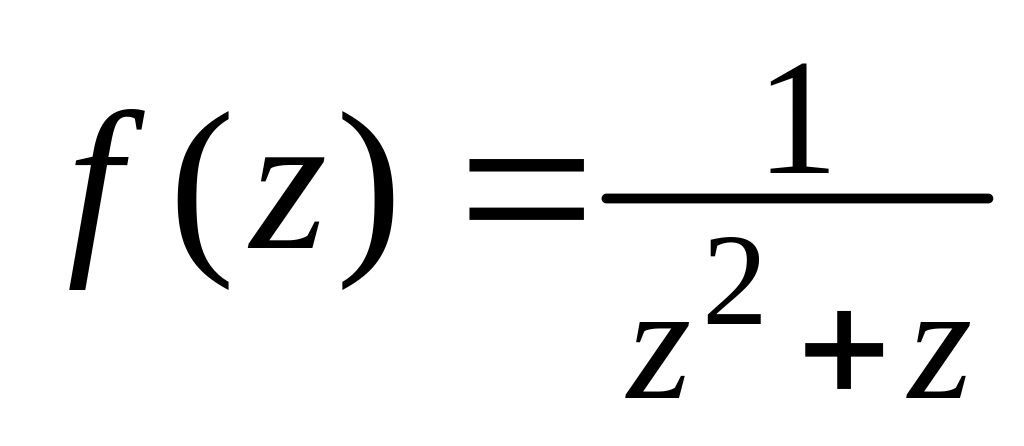 в ряд Лорана (
в ряд Лорана (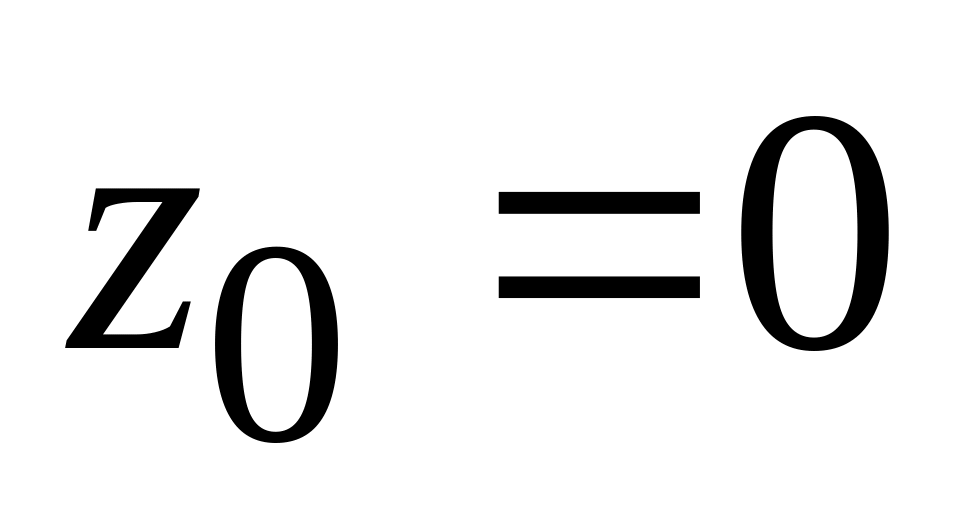 )
та вказати області в яких ці розвинення
справедливі.
)
та вказати області в яких ці розвинення
справедливі.Розв’язати інтегральне рівняння: .
Затверджено на засіданні кафедри математичного аналізу та теорії ймовірностей
протокол № 10 від „14” травня 2008 р.
Зав. кафедри Булдигін В.В. Екзаменатор Горленко С.В.
Національний технічний університет України „Київський політехнічний інститут”
(назва вищого навчального закладу)
Факультет ФМФ семестр 6
Навчальний предмет Теорія функцій комплексної змінної
Екзаменаційний білет № 4
Означення симетричних відносно кола точок та доведення властивості симетрії дробово-лінійної функції.
Теорема Руше: формулювання та доведення. Наслідок: основна теорема вищої алгебри (формулювання та доведення).
Обчислити
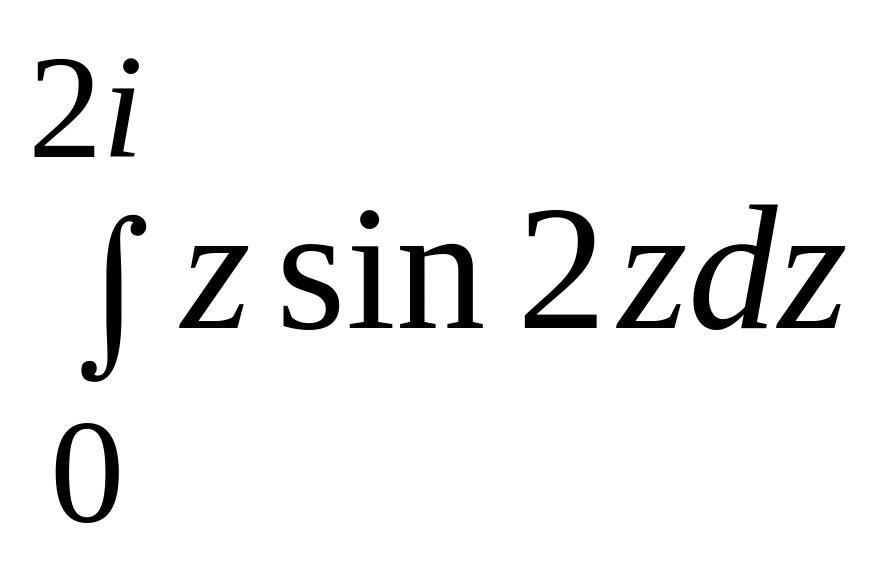 .
.Нехай
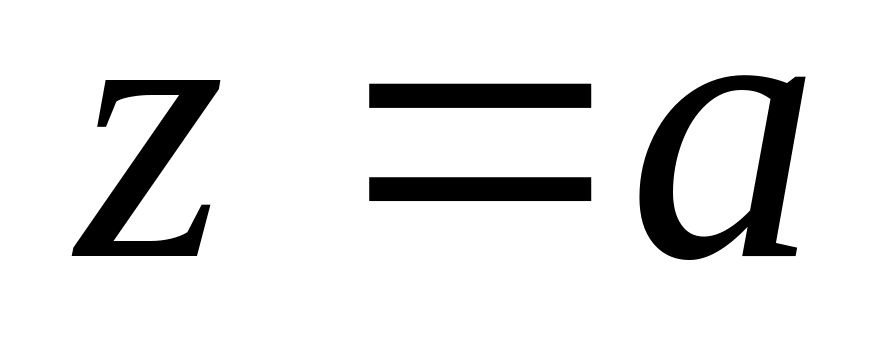 -
ізольована особлива точка для
-
ізольована особлива точка для
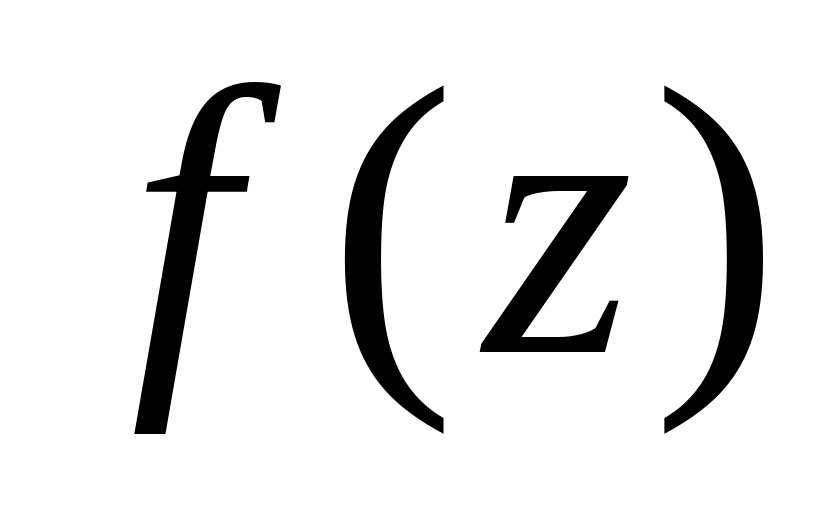 .
Довести, що якщо
.
Довести, що якщо
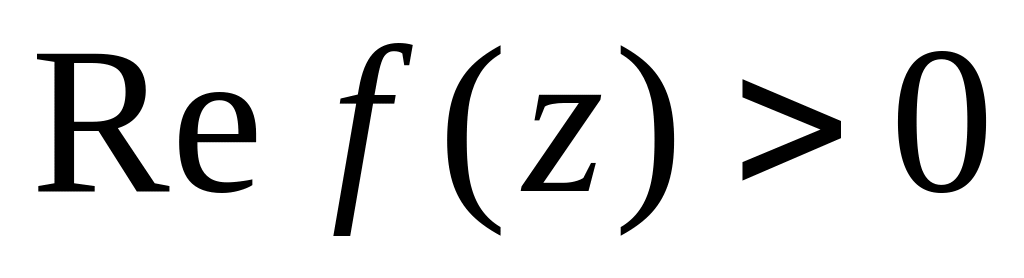 в деякому околі точки
в деякому околі точки
 ,
то ця точка є усувною (Вказівка: розглянути
допоміжну функцію
,
то ця точка є усувною (Вказівка: розглянути
допоміжну функцію
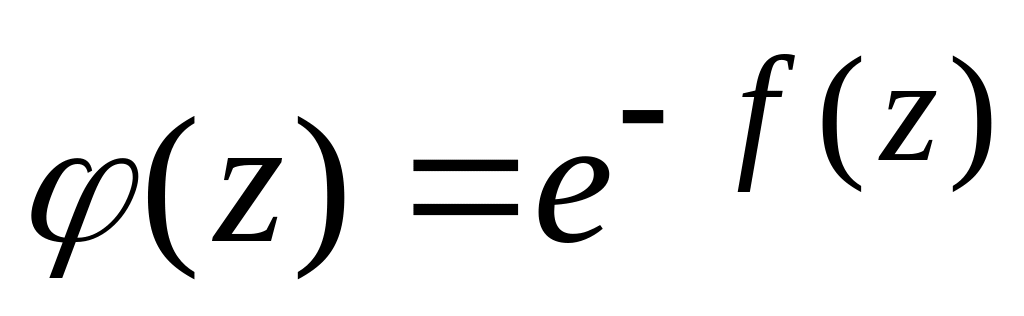 .
.Розв’язати задачу Коші:
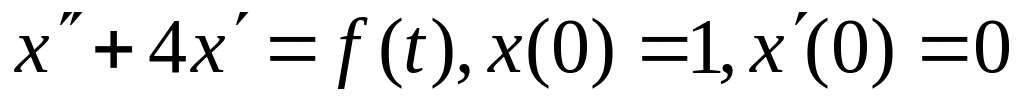 ,
де
,
де
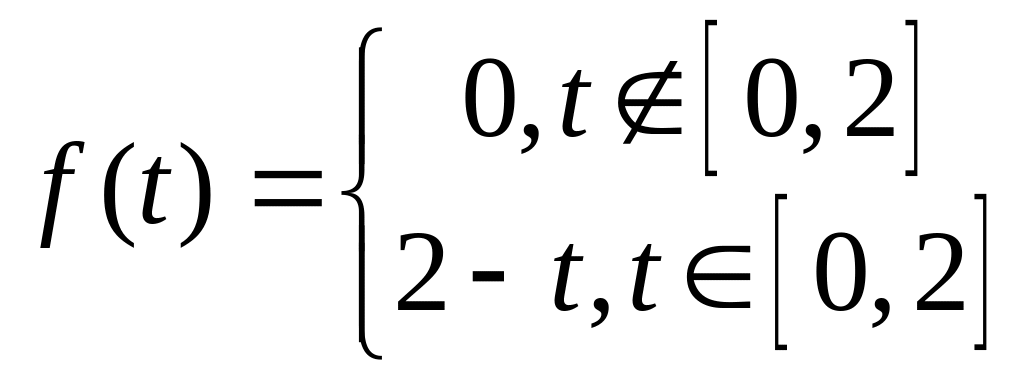 .
.
Затверджено на засіданні кафедри математичного аналізу та теорії ймовірностей
протокол № 10 від „14” травня 2008 р.
Зав. кафедри Булдигін В.В. Екзаменатор Горленко С.В.
Національний технічний університет України „Київський політехнічний інститут”
(назва вищого навчального закладу)
Факультет ФМФ семестр 6
Навчальний предмет Теорія функцій комплексної змінної
