Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Рекурсивная и адаптивная фильтрация

Файл:

Конспект по фильтрации

.pdf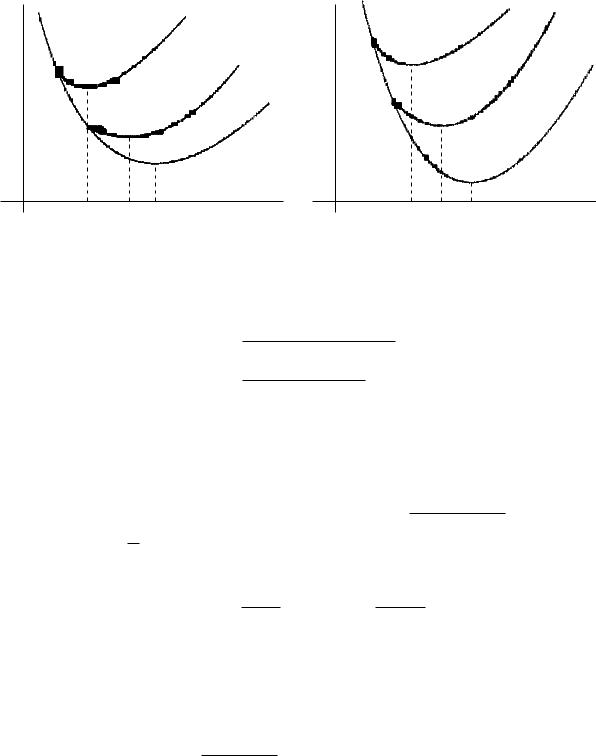

Скачиваний:

Добавлен:

01.05.2014

Размер:

675.33 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

Мальцева Н. В. Рекуррентная и адаптивная фильтрация					71
σ2	6		σ2	6
xn			x˙ n
	r			r
	r			r
	r			r
	r	-		r	-
	nm3 nm2 nm1	n		nm3 nm2 nm1	n

Ðèñ. 2:

ошибок оценок координаты σ2

σ2

x∞ и скорости

x˙ ∞ может быть записано в виде:

σ2

2kx2 − 3 kxkx˙

t + 2kx˙

σ2

kx(4 − 2kx − kx˙

x∞

(18.9)

kx˙ (2kx

kx˙

x˙

∞

−

kx(4 − 2kx − kx˙ t)

ãäå kx è kx˙ значения коэффициентов фильтрации в установившемся режиме, которые равны:

äëÿ Q-фильтра

√

+ 2r

1 + 2r

kx =

√1 + 2r − 1

;

kx˙ =

r2 −

ïðè r = 4σ √Q · t2 ;

äëÿ S-фильтра

kx =	s2 − 1	;	kx˙ =	1	(s − 1)2
	s2			t s2

На участке ман¼вра в оценках этих фильтров возникает смещение, вычисляемое по формулам (18.5). Однако оно в этом случае значительно меньше, чем смещение оценок РПД-фильтра.

Можно получить в установившемся режиме средние значения ошибок оценки коорди наты и скорости (ман¼вр окончен):

x∞

a t(1 − kx)

;

−

a t

kx˙

x˙ ∞

kx˙

ãäå kx è kx˙ значения коэффициентов усиления рассматриваемых фильтров в установив шемся режиме.

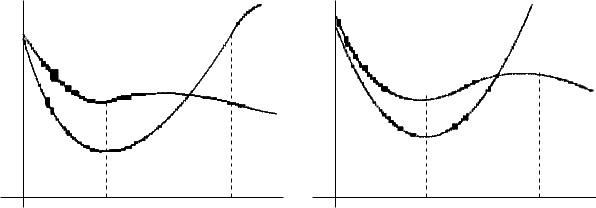
На рис. 3 приведены зависимости дисперсии действительной ошибки оценки координаты σxn и скорости σx˙ n от количества измерений для РПД и Q-фильтра. Параметры Q-фильтра были выработаны из условия минимизации ошибок оценки в установившемся режиме.

Мальцева Н. В.	Рекуррентная и адаптивная фильтрация				72
σ2 6	РПД-фильтр		6
σ2 6	r	σ2	6	РПД-фильтр
xn	r	x˙ n
xn		x˙ n
r	r Q-фильтр			Q-фильтр
r	r Q-фильтр
r
		-			-
nm	nk	n	nm	nk	n

Ðèñ. 3:

Из графиков видно, что Q-фильтр проигрывает в точности РПД-фильтру на участке

РПД, однако на участках ман¼вра он обеспечивает значительно лучшие точностные харак теристики. (Остальные фильтры к K∞ 6= 0 имеют при данном наборе параметров примерно такие же показатели).

При окончании ман¼вра фильтры с K∞ 6= 0 обеспечивают устранение накопленного за время ман¼вра смещения.

= Анализ свойств РПД-фильтра и его модификаций с K∞ 6= 0 позволяет заключить, что необходимо совместное использование различных методов обработки.

И наконец, для демонстрации явления расходимости , возникающего вследствие ошибок округления, рассмотрим два простых примера. Сравним дискретный фильтр Калмана и алгоритм Поттера при имитации округления результатов сч¼та.

Èòàê,

1.	Пусть модель системы имеет вид:				0 1 x2				(k)
			x2	(k + 1) =	0 1 x2				(k)
			x1	(k + 1)		1 0 x1			(k)
2.	Пусть две модели измерений:					x2	(k)
			y(k) = 1 0			x2	(k)	+ vk
						x1	(k)
						x2	(k)
			y(k) = 1 1			x2	(k)	+ vk
						x1	(k)

3.	Пусть априорная информация:			P0 = 0 1				vk N(0, ε2) ; ε 1
	x2	(k) N	0 , P0 ;	P0 = 0 1			;	vk N(0, ε2) ; ε 1
	x1	(k)	0	1		0
4.	Пусть имитация округления результатов сч¼та:
			1 + ε 6= 1 ;	1 + ε2r ≈ 1			ïðè		r = 1, 2, . . .

(18.10)

(18.11)

(18.12)

(18.13)

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

Напомним, что алгоритм Поттера имеет следующий вид:

x(k|k − 1) = Φ(k|k − 1)x(k − 1|k − 1)

S(k|k − 1) = Φ(k|k − 1)S(k − 1|k − 1)

P (k|k − 1) = S(k|k − 1)ST(k|k − 1)

−

x(kK| k

= αkS|(k−k 1)Fkk

k −

k) = x(k k 1) + K y

x(k

−

S(k|k) = S(k|k − 1) I − αkγkFkFkT

P (k k) = S(k k)S

(

T k

Fk = ST(k|k − 1)HkT ,

ãäå

αk = FkF T

+ Rk

−1

γk

= 1 + k

Rkαk

−1

Ниже в таблице приведены коэффициенты усиления и ковариационные матрицы первых двух шагов фильтра Калмана и Поттера.

	Реализация
алгоритма								Модель дискретных измерений (18.11)
	оценивания
				K1									P (1\|1)														K2			P (2\|2)
(точные			1 + ε2				0					1 + ε2					0								2 + ε2				0	2 + ε2					0
Алгоритм Калмана			1										ε2				1									1					ε2				1
	результаты)											0					1														0				1
							1																						1
Алгоритм Калмана				0								0			1												0			0
	округления			0								0			1												0			0			1
с имитацией		1										0			0													0			0		0
с имитацией

с имитацией		0						S(1 1) ST(1 1) =										0			1					2		0			2			0
Алгоритм Поттера		1																	ε2		0					1		1			ε2
	округления							\|		×				\|																	0		1


	Реализация
	алгоритма							Модель дискретных измерений (18.12)
	оценивания
					K1												P (1\|1)															K2
	Алгоритм Калмана		1				1					1					1 + ε2						−1								1				1
							1											−1				1 + ε2													1
	(точные результаты)			1 + ε2			1						2 + ε2					−1				1 + ε2								4 + ε2					1
	Алгоритм Калмана		2			1										2	−1				1											0
	округления		2			1										2	−1				1											0
	с имитацией		1			1										1		1			−1												0
	с имитацией																				−1
	Алгоритм Поттера с								\|		·				\|			2		−1			1
								S(1		1)		ST(1				1) =			1		1		−1
			2			0		S(1		1)		ST(1				1) =					1 +		−1				√2		− 1		3		1
	округления		2			0												1			1 +		√2				√2		− 1		3		1
	имитацией		1			1																		ε				ε			1		1
													S(1 1) =								ε								ε
															\|						√2 − 1 1 + √2

																			2

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

19 Фильтрация при наличии аномальных измерений

До сих пор при синтезе алгоритмов оценивания вектора состояния xt динамической си стемы мы предположили, что в выборке измерений Y1k содержится информация об оценива ниваемом векторе xt и полностью известны статистические характеристики погрешностей измерений и шумов динамической системы. При решении практических задач встречаются ситуации, когда возможно появление измерений, не содержащих информации об оценивае мом векторе состояния xt. Такие измерения называют аномальными. Эти ситуации могут определяться:

пропуском измерений;

появление ложных измерений;

возникновение неисправностей.

= Если использовать алгоритмы, не учитывающие возможность появления аномаль

ных измерений, можно получить существенно смещ¼нные оценки и даже срыв сопрово ждения в задачах радиолокации.

Рассмотрим здесь из множества задач оценивания аномальных измерений только две, в которых будет предполагаться, что известно априорное статистическое описание скач кообразного процесса , входящего в модель измерений, но построение оценки самого скачко образного процесса не требуется .

Алгоритм (Фильтрации при независимых значениях переменных переключе ния). Äàíî:

1. Модели системы:

xk+1 = Φ(k + 1|k)xk + (k + 1|k)wk

2. Модель дискретных измерений:

yk = γkHkxk + Bkvk

3. Априорные значения:						cov(vk, vj) = Rkδkj ;
cov(wk, wj) = Qkδkj ;						cov(vk, vj) = Rkδkj ;
	x0	N x(0, 0), P0			; wk N(0, Qk) ; vk					N(0, Rk) ;
cov(wk, vj) = cov(x0, wk) = cov(x0, vk) = 0 ; k, j = 1, 2, . . .




			1	с вероятностью			qk;
			1				qk;

	γ	=	0 с вероятностью 1 − qk;
	k	(	0 с вероятностью 1 − qk;

	γk	не зависит от			x0	, wk, vk		è	γj, j = k	.
	γk				x0	, wk, vk			γj, j = k
									6
									6

(19.1)

(19.2)

(19.3)

Доказать:

Алгоритм фильтрации зада¼тся рекуррентными соотношениями:

−

−1

x(k

= x(k

+ Kk

qkHkx(k

1) ;

(19.4)

= qkP (k k

1) bk

k k k

−

k k k

(19.5)

| −

1) + (1

H q H q P (k

q )S(k

1) H + B R B

;

P (k k)

= (I

q K

)P (k

1) ;

(19.6)

P (0||0) = P0

−

k bk

−

Мальцева Н. В. Рекуррентная и адаптивная фильтрация 75

Алгоритм экстраполяции зада¼тся соотношениями стандартного фильтра Калмана

è
S(k + 1\|k) = Φ(k + 1\|k)S(k\|k)ΦT(k + 1\|k) + (k + 1\|k)Qk T(k + 1\|k)	(19.7)

ïðè S(0|0) = P0 + x(0|0)xT(0|0), ãäå S(k + 1|k) = Exγ[xk+1xTk+1|Y1k].

Доказательство. В данной задаче по выборке измерений Y1k требуется найти оценку пер вой компоненты вектора состояния {xk, γk}. Вторая компонента является мешающим пара метром и оценке не подлежит. Т. к. выполнены уловия (19.3), то для одношаговой процеду ры оценивания применяется теорема о нормальной корреляции.

Введ¼м следующие обозначения:
















		h
		h
		xk
Exγ		xk
	xγ	x
E		k


		h
		h

		y	k
Exγ			k


		h
		h

Exγ[xk|Y1k] = x(k|k) ;

Exγ[xk|Y1k−1] = x(k|k − 1) ;

Exγ h xk − x(k|k) xk − x(k|kT

Y1 i

= P (k|k) ;

)

−

x(k k

1) xk

−

x(k k

Y1 −

= P (k

−

1) ;

(19.8)

| −

−

Exγ

[yk

] = y(k

1) ;

− x(k|k − 1) yk

−

− y(k|k − 1) T Y1k−1i

= Pxy(k|k − 1) ;

−

y(k k

1) yk

−

y(k k

Y1 −

= Pyy(k k

1) ;

| −

Запишем соотношения теоремы о нормальной корреляции применительно к рассматри ваемому случаю:

K| k

= Pxy|(k k

1)Pyy−1(k k 1) ;

(19.10)

x(k k) = x(k k

−

1) + Kk

− y(k|k − 1)

;

(19.9)

P (k|b

| −

−

k) = P (k

P T

(19.11)

При этом, заметим, что

E γk

= qk · 1 + (1 − qk) · 0 = qk ;

(19.12)

E γk2

= qk · 12 + (1 − qk) · 0

= qk ;

(19.13)

Вычислим отдельно величины y(k|k − 1), Pxy(k|k − 1), Pyy(k|k − 1). Используя вид модели

измерений (19.2), обозначения (19.8), вид E γk è E γk2				(19.12) (19.13), и, наконец, независи
мость γk îò x0, wk, vk è γj, j 6= k (условие (19.3)), получим:
y(k\|k −	1)	= Exγ[γkHkxk + Bkvk\|Y1k−1] = qkHkx(k\|k − 1)				(19.14)
Подставим теперь значение			èç
yk − y(k\|k −	1)	= Hk	γkxk − qkx(k\|k − 1)		+ Bkvk	(19.15)

yk − y(k|k − 1) последнего соотношения (19.15) в выраже ние (19.8) для определения Pxy(k|k − 1) è Pyy(k|k − 1) и, учитывая вид априорных дан

ных (19.3) и значения E γk (19.12) è E γk2		(19.13), определяем:
Pxy(k\|k − 1) = Exγ h	xk − x(k\|k − 1) γkxk − qkx(k\|k − 1)				THkT+
		T	T		k	1	T
	+ xk − x(k\|k − 1) vk		Bk	Y1 −		i	= qkP (k\|k − 1)Hk (19.16)
		\|{z}
		\|{z}

Мальцева Н. В. Рекуррентная и адаптивная фильтрация

Pyy(k|k − 1) = Hk Exγ h γkxk − qkx(k|k − 1) γkxk − qkx(k|k − 1) T Y1kiHkT + BkRkBkT =

= Hk

Exγ

γk

x(k

1) + (γk

qk)x(k k

−

−T

| − T

− | −

−

| −

x(k k

1)) + (γk

qk)x(k k

Hk + BkRkBk

= раскрыли скобки

γk(xk

= Hk Exγ

γk

−

x(k

−

x(k

−

1) +

+γk(γk − qk) xk − x(k|k − 1) xT(k|k − 1) + γk(γk − qk)x(k|k − 1) xk − x(k|k − 1) T+

+ (γ

k −

)2x(k

−

1)xT(k

−

Y k−1

HT + B

R BT = бер¼м мат. ожидание

= Hk

qkP (k

−

1) + E(γk2

−

2γkqk + qk2)

x(k k

−

1)xT(k

−

1) Y k−1

HkT + BkRkBkT =

qkP (k

−

1) + qk(1

−

qk)x(k

−

1)x (k k

k k k

= H

−

+ B R BT ; (19.17)

имеем:

Pyy(k|k − 1) = qkHk qkP (k|k − 1) + (1 − qk)S(k|k − 1) HkT + BkRkBkT .

(19.18)

Подставляя полученные выражения для y(k|k − 1) (19.14), P (k|k − 1) (19.16) и Pyy(k|k − − 1) (19.18) в соотношения (19.9) (19.11), получим требуемые равенства (19.4) (19.6).

Алгоритм (Фильтрации при постоянных значениях переменных переключения на интервале наблюдения). Äàíî:

1. Модели системы, дискретных измерений и априорная информация вида (19.1) (19.3).

2.	(	0	с вероятностью	1k	qk;
γk = γ =
		1	с вероятностью	q	;

−

γ = const , γ не зависит от x0, wk, vk. Доказать:

1. Алгоритм фильтрации значений x(k|k) = E(xk|Y1k) è P (k|k) = cov(xk, xk|Y1k) имеет

âèä:

−

k −

−

x(k

T −1

k) = x(k

1) + Kk y

x(k

k = qkP (k

−

1) bk

k qkP (k

−

1)Hk + Bk kBk

P (k b

−

k k

k) = (I

1) + (1

P (0

0) = P ;

K H )P (k

q)K H S ;

2.Алгоритм экстраполяции значений

зада¼тся рекуррентными соотношениями стандартного фильтра Калмана и (19.7).

Доказательство. Доказательство аналогично предыдущей теореме.

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

Исследование алгоритмов с использованием аномальных измерений на конкретных при мерах показало, что оценки x(k|k) существенно зависят от априорных допущений, приня

тых для вероятности qk, с которой появляется значения γk = 1. Поскольку на практике за частую характер измерительной информации не соответствует допущениям относительно параметра γk = алгоритмы с фиксированными значениями γk оказываются недостаточ но эффективными. Одним из путей улучшения качества работы алгоритмов оценивания является разработка робастных алгоритмов оценивания. Они незначительно уступают

âэффективности классическим алгоритмам оценивания при точном выполнении условий оптимальности, но в отличие от классических робастные алгоритмы при малых отклоне ниях от предположений о модели системы или измерений ухудшают качество оценок лишь

âмалой степени.

Привед¼м один из возможных робастных алгоритмов рекуррентной фильтрации для оценки скалярного случайного процесса по скалярным измерениям.

Алгоритм (Робастный алгоритм Ершова Линцера). Äàíî:

1. Модели системы:

xk+1 = a0(k) + a1(k)xk + a2(k)yk + wk+1

2. Модель измерений:

yk+1 = A0(k) + A1(k)xk + A2(k)yk + (1 − λk+1)vk+1 + λk+1εk+1

3. Априорные данные и начальные условия:
	wk+1 N(0, Qk+1) ;					vk+1 N(0, Rk+1) ;
cov vk	εk+1 N(0, Dk+1) ;			cov	εk	, εj	x0 N(¯x0, P0) ;
cov vk	, vj	= CkT	Rk δkj ;	cov	εk	, εj	=	0	Dk δkj
wk	wj	Qk	Ck		vk	vj		Rk	0
Кроме того, случайные величины λk принимают независимые значения 0 èëè 1;
Последовательность		{(λk); k	= 1, 2, . . . } и гауссовская случайная величина x0 íå
зависят от {(wk), (vk), (εk), k = 1, 2, . . . } è y0.

4. Дополнительные ограничения алгоритм оценки параметра

λk+1 зада¼тся в следу

þùåì âèäå:

= (

|Λk+1|

λk+1

0 ,

ïðè

< c(k, α) ,

ãäå

1 ,

ïðè

Λk+1

> c(k, α)

Λb

= y

k+1

−

(k)

(k)y

;

k+1

− A1(k)bk −

nk+1 = a0(k) + a1(k)nk + a2(k)yk ;

n0 = x¯0 .

Константа bc(k, α)

выбирается исходя из задания уравнения ложной тревоги

α:

P |Λk+1| > c(k, α) λk+1 = 0

= α

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

Доказать, что условное математическое ожидание

x(k|k) = E(xk|Y1k, λ1k

= λ1k) и услов

ная корреляционная матрица P (k|k) = cov(xk, xk|Y1 , λ1 = λ1) удовлетворяет b

следующим

соотношениям:

− A2(k)yk

b |

k) + a2(k)y

+ K

k+1

A0(k)

−

b |

−

;

k+1 −

x(k + 1

k + 1) = a0(k) + a1(k)x(k

(k)x(k k)

P (k + 1 k + 1) = a2(k)P (k k) + Qk

Kk+1

(1 λk+1)Ck + a1(k)P (k k)x(k k)A1(k) ;

k+1

− b

k+1

−

−b

k+1

+ 1

K = (1 λ )C + a1(k)P (k k)x(k k)A1(k) (1 λ )Rk

+ λ Dk+

x(0 0) = x¯0

;

P (0 0) = P0 .

(k)P (k k)

ãäå

Доказательство b

Доказательство.

аналогично предыдущим (если частный случай от

сутствие корреляции шумов модели системы и измерений), либо с использованием более громоздких формул (опускаем).

Можно также показать, что функция распределения P (|Λk+1| > bc(k, α) λk+1 = 0) ÿâëÿ

ется гауссовской и имеет параметры (0, A21(k) k + Rk), ãäå = E(xk − nk)2 определяется рекуррентным соотношением k+1 = a21(k) k + Qk; 0 = P0.

Сравнение результатов работы робастного алгоритма с алгоритмами, не учитывающими аномальные измерения, и с алгоритмами, учитывающими их с априорным предположением, ÷òî P (λk = 1) = qk, показывают эффективность предложенного алгоритма.

Мальцева Н. В. Рекуррентная и адаптивная фильтрация 79

Содержание

1		Введение	1
2		История	2
3	Общая формулировка задачи оценивания		3
4	Критерий оптимизации при вероятностном подходе		5
5	Критерий оптимизации при наличии априорной неопредел¼нности		11
6		Элементы теории оценивания	12
7	Оптимальные линейные алгоритмы оценивания при полной априорной ин
		формации	15
8	Вычислительная схема стандартного фильтра Калмана		17
9		Фильтрация стационарных сигналов	20
10		Фильтрация сигналов в нелинейных системах	26
11		Использование алгоритмов рекуррентной фильтрации для решения зада
		чи определения координат и параметров движения объектов	31
12		Расч¼т эффективности алгоритма оценивания по результатам моделиро
		вания	37
13		Алгоритм определения координат и параметров движения маневрирую
		щего объекта по пеленгам	39
14		Синтез устойчивых алгоритмов фильтрации	42
15		Последовательная обработка дискретных измерений	48
16		Методы фильтрации на основе использования квадратных корней из мат
		ðèö	53
17		Интерполяция компонент гауссовских процессов	60
18		Расч¼т действительной точности линейных фильтров	68
19		Фильтрация при наличии аномальных измерений	74

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

Соседние файлы в предмете Рекурсивная и адаптивная фильтрация

#
01.05.2014675.33 Кб84Конспект по фильтрации.pdf
#
01.05.20141.06 Mб28Лабораторная работа.doc