Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Рекурсивная и адаптивная фильтрация

Файл:

Конспект по фильтрации

.pdf

Скачиваний:

Добавлен:

01.05.2014

Размер:

675.33 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Мальцева Н. В. Рекуррентная и адаптивная фильтрация 21

Пример 2. Пусть дана стационарная скалярная система:

xk = xk−1 + wk y = xk + vk ,

ãäå wk è vk стационарные белые последовательности с нулевым средним и дисперсиями q = 25 и r = 15 соответственно.

Пусть начальная оценка дисперсией P0 = 100. Тогда

P (k\|k − 1) =	Pk−1 + 25 ;			èç (2.3)	(прогноз P )
Kk = (Pk−1 + 25)/(Pk−1 + 40) ;				èç (2.4)	(коэффициент усиления)
Pk =	15(pk−1 + 25)		= 15 · Kk ;	èç (2.5)
Pk =		(pk−1 + 40)	= 15 · Kk ;

{Pk = r(pk−1 + q)/(pk−1 + q + r)}

Начиная с Pk−1 = P0 = 100, сравнительно просто вычислить P (k|k − 1), Pk è Kk äëÿ k = 1, 2, . . . Результаты нескольких первых вычислительных циклов сведены в таблицу 1.

k	P (k\|k − 1)	Kk	Pk
0	−	−	100
1	125	0.893	13.40
2	38.4	0.720	10.80
3	35.8	0.704	10.57
4	35.6	0.703	10.55

Таблица 1: Практическая таблица

Теоретически рассчитанное установившееся значение Pk можно получить, подставляя значение Pk = Pk−1 = P в последнее из тр¼х привед¼нных соотношений:

P = 15(P + 25) P 2 + 40P = 15P + 375 P 2 + 25P − 375 = 0 .

P + 40

Поскольку P дисперсия = единственный корень P = 10.55 = из таблицы 1 видно,

что фильтр находится в установившемся состоянии в пределах имеющейся точности уже после обработки 4-х измерений. Это означает, что уравнение фильтра

xˆk = xˆk−1 + 0.703(yk − xˆk−1) = 0.297ˆxk−1 + 0.703yk

находится в установившемся состоянии для k = 4, 5, . . .

Пример 3. Рассмотрим линейную дискретную систему вида:

(

Xk+1 = ΦkXk

t = const.

Yk = HkXk + ξk ,

Мальцева Н. В. Рекуррентная и адаптивная фильтрация

Пусть xk R2.

à) Xk = (xk, x˙ k)

á) Xk = (x0, x˙ 0)

Φk

= 0 1t

Φk = 0 1

= x0

+ x˙ 0

= x0

= (1 0)

= x

+ 2Δtx˙

= (1 (k 1)Δt)

−

y .

= x

+ (k 1)Δtx˙

−

Хотим построить оценку на текущий момент времени tk = надо воспользоваться подхо дом б).

Для простоты вычислений оценку Qk получим, заменив систему а) ей эквивалентная:

[t1, . . . , tk]	yk = xk	Xk = (xk, x˙ k)
{y1, . . . , yk}	yk−1 = xk − tx˙ k
	yk−2 = xk − 2Δtx˙ k

...

yk−(k−1) = xk − (k − 1)Δtx˙ k

| {z }

Hk = (1 − (k − 1)Δt) = далее применяем МНК.

Единичной матрицей обычно стараются делать либо Φk, ëèáî Hk.

Для простоты вычислений рассмотрим систему б), т. е. фильтрацию параметров. Вос пользуемся в этой постановке формулами метода наименьших квадратов (МНК), которые

для данного класса задач обеспечивают построение требуемых оценок. Итак, Pn = σ2 · Qn, ãäå Qn = (HnTHk)−1

1		−0 t			1	1 . . .
	1
Hn = 1.		−2Δ.	t	Qn−1 = HnTHn =	0	t		2Δt . . .
	.	.				−	−
.		.				−	−

1		(k 1)Δt

		− −

1		− t
1			0
1.		−2Δ.		t
..			..

			n(n 1)
1		t	2−
	−

1)Δt (1

− (k − 1)Δt) =

= k=1

−

1)Δt

(k 1)2 t2

tn(n−1)

(n−1)(n−2)n !

k=1

−(k − 1)Δt

−

n(n−1)

X −

−

Мальцева Н. В. Рекуррентная и адаптивная фильтрация

det Q

t2n(n − 1)(n − 1)

−

t2n2(n − 1)2

t2n2(n − 1)[4n − 2 − 3n + 3]

t2n2(n − 1)(n + 1)

;

Q11

t2(n − 1)n(2n − 1) · 12

2(2n − 1)

;

n(n + 1)

6Δt2n2(n − 1)(n + 1)

Qn22 =

n · 12

;

t2n2(n2

t2n(n2 − 1)

− 1)

Qn12 =

t · n(n − 1) · 12

;

Èòàê,

2Δt2n2(n − 1)(n + 1)

tn(n + 1)

Pn = σ

· "

tn(6n+1)

2 12

# =

σ212

σ222 .

2(2n−1)

def

σ2

t n(n −1)

n(n+1)

tn(n+1)

Найд¼м вид коэффициентов усиления Kn

Kx˙ n+1

Kxn+1

n+1

= P (n + 1

n)HT (H

n+1

P (n + 1

n)HT

+ σ2)−1 .

n+1

С этого момента начн¼м фильтровать текущий вектор, т. е. вектор, задаваемый соотноше

íèåì (à) (xk, x˙ k) è Hk = (1				0)T соответственно.
Тогда
\|	1	t	σ2	σ2	1	0		σ2	+ 2Δtσ2 + t2σ2		σ2 + tσ2
\|	0	1	σ212	σ222	t	1		11	σ122 + tσ222	22	σ222
P (n + 1 n) =			11	12			=	11	12	22	12	22 .

Подставим значения σ11, σ12, σ22 в уравнение

σ112

Èòàê,

+ 2Δtσ2 +

t2σ2

2(2n − 1)

2Δt · 6

t · 12

···

2(2n + 1)

;

n(n + 1)

tn(n + 1)

n(n − 1)

t2n(n2 − 1)

σ122 + tσ222

12Δt

= ··· =

;

tn(n + 1)

t2n(n2 − 1)

tn(n − 1)

P (n + 1 n) =

6−

12 −

σ ,

Kn+1

σ122

t n(n−1)

t2n(n2−1) !

σ112

+σ2

2(2n+1)

σ112

n(n 1)

t n(n 1)

σ112 +σ2

Тогда

Kn+1 =

Èòàê, оценка xk è x˙ k

6−	. 2(2n+1)			=		=	6	.
2(2n+1)		2(2n+1)		+ 1	···		t(n+1)(n+2)	!
t·n(n−1)		. n(n−1)		+ 1	···		t(n+1)(n+2)	!
			+ 1				2(2n+1)
n(n 1)		n(n−1)	+ 1				(n+1)(n+2)

может быть построена по следующим формулам:

k−1

k(k + 1)

−

k−1 −

k−1

= x

+ x˙

t +

2(2k − 1)

yèçì.

x˙

èçì

= x˙ k−1 +

− xk−1

− x˙ k−1

x˙ k

t · k(k + 2) yk

cov Xk =	2(2k−1)	6
	k(k+1)	t k(k+1)
	6	12
	t k(k+1)	t2k(k2−1)

, ãäå Xk =	x˙ k
	xk

= поведение cov Xk è Kk с увеличением k, зависимость от t.

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

Пример 4. Рассмотрим тр¼хмерную дискретную систему, т. е.

x˙ k			= x˙ k−1	+ x¨k−1	t	−
	xk		= xk 1	+ x˙ k 1	t + x¨k		1
			−	−
x¨		k	= x¨
		k	k−1

t2/2	Φk =	0	1t	t	2
					t/2
		1
=		0	0	1

Hk = (1 0 0)

σ2

3(3n2 − 3n + 2)

σ2

n(n + 1)(n + 2)

12(2n 1)(8n

11)

σx2

−

4)(n

1)n

−

σx23 =

720

4 σ2

n(n

4)(n

1)Δt

−

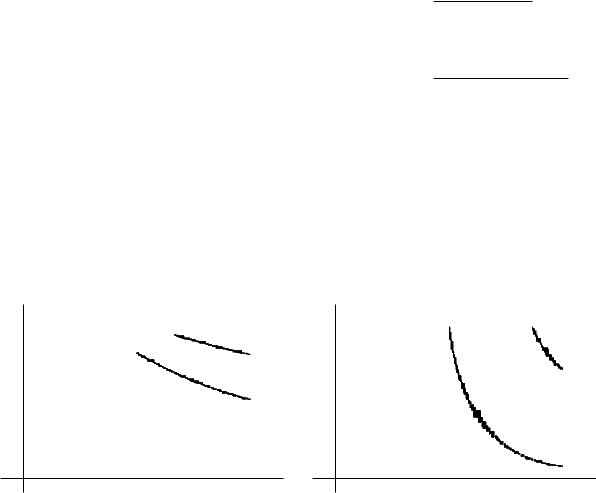
Сравним точности оценивания для 2-х и 3-х мерной модели (в разах от σ2)

	2-x ìåð.		3-x ìåð.
	x1	x2	x1	x2
n = 1	1	−	1	−
n = 2	1	6	1	−
n = 3	0.83	1	1	6.5
n = 4	0.7	0.33	0.95	2.45
n = 5	0.6	0.15	0.88	1.24
n = 6	0.52	0.08	0.82	0.72

1	6σx1			q	3-x ìåð.		1	6σx2		q
	2							2
			q	q	q	q							3-x qìåð.
0.5			2-x ìåð.	q	q	q	0.5						3-x qìåð.
0.5			2-x ìåð.		q	q	0.5				q
											q	q
						-n				2-x ìåð.		q	q	-n
0	1	2	3	4	5	6	0	1	2	3	4	5	6

= Выводы:

1)на небольших участках наблюдения траекторию целесообразно приближать полино мом 1-й степени (существенно выше точность, а не динамические ошибки ещ¼ не успеют сказаться);

2)видно, что теряем на загрубении модели.

Найд¼м другой вид оценок двумерной системы, при котором оценки xk è x˙ k могут быть записаны в виде линейных функций от {yièçì.} с соответствующими весовыми коэффици

ентами.

Мальцева Н. В. Рекуррентная и адаптивная фильтрация

Пример 5. Рассмотрим систему

( yk

= HkXk + ξk

= (1

1)Δt)

= X

k−1

= (x

x˙

èçì.

−

Пусть t = const =

èçì.

= x0

+ x˙ 0(k − 1)Δt + ξk .

По МНК следует минимизировать функционал

Jn =

− x0 − x˙ 0(i − 1)Δt)

èçì.

(yi

= система уравнений, подлежащая решению, будет следующая

(yi

− x0 − x˙ 0(i − 1)Δt) = 0

i=1

èçì.

(yèçì

x˙ (i

1)Δt)(i

1)Δt = 0

− 0 − 0

−

Решая эту систему относительно x0 è x˙ 0, можно получить:

x =

4n + 4 − 6i

yèçì.

n(n + 1)

x˙

12i − 6n − 6

yèçì.

t n(n2

−

На текущий момент времени имеем:

x =

4n + 4 − 6i

yèçì. =

a (i) yèçì.

n(n + 1)

· i

i=1

x˙ =

12i − 6n − 6

yèçì. =

b (i) yèçì.

t n(n2

−

1) · i

· i

i=1

Небольшое отступление

Пример 6. Рассмотрим одномерную систему:

( yk

= xk + ξk .

= xk−1

Оценивая xk с постоянным коэффициентом α по формулам фильтра Калмана, имеем:

xk = xk−1 + α(yk − xk−1)				0 < α < 1
	k		k
xk	Xi	X
xk	=	α(1 − α)iyk−i =	ηi yk−i	x0 = 0
	=0		i=0

ηi весовая функция, ηi = α(1 − α)i имеет вид экспоненты

Мальцева Н. В. Рекуррентная и адаптивная фильтрация

0.9

α = 0.9

0.5

α = 0.5

α = 0.1

0.1

yk−4 ←− yk−3 ←− yk−2 ←− yk−1 ←−

10 Фильтрация сигналов в нелинейных системах

Во многих практически важных случаях физические системы и взаимосвязь измеряе мых параметров с оцениваемыми нельзя описать линейными уравнениями или линейными рекуррентными соотношениями, для этой цели следует использовать системы нелинейных уравнений èëè нелинейных рекуррентных соотношений .

Решение задачи фильтрации в случае нелинейных моделей состояния и измерения мо жет быть получено, например, с использованием теории условных марковских процес сов, разработанной Стратановичем. Эта теория характеризуется математической строго стью методов, базируется на аппарате многомерных плотностей распределения вероятно стей и байесовском подходе . Получающееся при этом точное решение оказывается слишком сложным в вычислительном отношении для того, чтобы его можно было использовать при обработке сигналов в реальном масштабе времени. Точные алгоритмы нелинейной фильтра ции, представляющиеся в общем случае бесконечномерными цепочками уравнений , подвер гаются различным аппроксимациям с целью получения конечномерных вычислительных алгоритмов, реализация которых на ЭВМ не составляет проблемы.

Получающиеся при этом алгоритмы нелинейного оценивания могут быть также выведе ны пут¼м эвристического обобщения на нелинейный случай алгоритма линейного фильтра Калмана. Это обобщение выполняется на основе линеаризации нелинейных моделей с помо щью разложения нелинейных зависимостей в ряды Тейлора. В разложениях, как правило, используется только члены первого порядка и лишь иногда ещ¼ и члены второго поряд ка (фильтр второго порядка). Именно таким способом мы и получим простые алгоритмы фильтрации.

Дискретный линеаризованный фильтр Калмана

Особенность данного подхода заключается в том, что предполагается известной опор ная траектория, т. е. значение оцениваемых параметров для любого момента времени, достаточно близкие к истинным.

Äàíî:

1.	Модель системы:
	xk+1 = f(xk) + b(xk)wk ;	(10.1)
2.	Модель измерений:
	yk+1 = h(xk+1) + B(xk+1)vk+1 ;	(10.2)

Мальцева Н. В.		Рекуррентная и адаптивная фильтрация				27
3.	Априорная информация:
		x0 N(¯x0, P0) ;	wk N(0, Qk) ;		vk N(0, Rk) ;	(10.3)
		cov(wk, wj) = Qkδkj ;		cov(vk, vj) = Rkδkj ;
		cov(wk, vj) = cov(x0, wk) = cov(x0, vk) = 0
4.	Выборка измерений:
		Y1k = {ys : s = 1, . . . , k};
5.	Опорная траектория:
		xn	= f(xn) ;	xn	= x¯0 ;	(10.4)
		k+1	k	0

6.Аппроксимирующие предложения:

Функции f(xk), b(xk), h(xk+1), B(xk+1) раскладываются в ряды Тейлора соответ ственно в окрестности точек xnk è xnk+1;

Пренебречь значениями (xk − xnk )wk, (xk+1 − xnk+1)vk+1, o(xk − xnk ), o(xk+1 − xnk+1) и статистическими моментами третьего и выше порядка;

o(·) бесконечно малая величина относительно своего аргумента.

Доказать:

1. Алгоритм экстраполяции значений

x(k + 1|k) = E(xk+1|Y1k)

P (k + 1|k) = cov(xk+1, xk+1|Y1k)

имеет вид:

x(k + 1 k) = xn

∂f

x=xkn

(x(k k)

xn)

(10.5)

k+1

∂x

−

∂f

P (k + 1|k) =

x=xn · P (k|k)

n + b(kk )

· Qk

(xk )

(10.6)

∂x

x=x

2. Алгоритм фильтрации значений

k+1

)

P (k + 1|k + 1) =

k+1

x(k + 1|k + 1) = E(xk+1|Y1

= cov(xk+1, xk+1|Y1

) зада¼тся рекуррентными соотношениями:

x(k + 1|k + 1) = x(k + 1|k) + Kk+1 "yk+1

− h(xkn+1) −

∂h

(x(k + 1|k) − xkn+1)# ;

∂x

x=xn

k+1

Kk+1 = P (k + 1|k)

x=xn

(10.7)

∂h

∂x

k+1

∂h

+ B(xkn+1)Rk+1BT(xkn+1)

−

· P (k + 1|k) ·

∂x x=xn

∂x

k+1

x=xk+1

(10.8)

P (k + 1|k + 1) =

I − Kk+1

∂h

! · P (k + 1|k) ;

(10.9)

∂x

x=xn

k+1

Мальцева Н. В.	Рекуррентная и адаптивная фильтрация				28
Доказательство : Введ¼м следующие обозначения:
def	− xkn ;	def	def	− h(xkn+1) .
xk = xk	− xkn ;	xk+1 = xk+1 − xkn+1 ;	yk+1 = yk+1	− h(xkn+1) .	(10.10)

Т. к. значение x¯0 неслучайно и соотношение (10.4) (опорная траектория) детерминировано, то, вычисляя условное математическое ожидание E( ·|Y1k) выражений (10.10), получим:

x(k\|k) = x(k\|k)−xkn ;		x(k+1\|k) = x(k+1\|k)−xkn+1 ;			y(k+1\|k) = y(k+1\|k)−h(xkn+1) ;
						(10.11)
Из (10.11) следует:
	x(k\|k) = xkn +		x(k\|k) ;	x(k + 1\|k) = xkn+1 + x(k + 1\|k) ,		(10.12)
ãäå	x(k\|k) = E(Δxk\|Y1k) è		x(k + 1\|k) = E(Δxk+1\|Y1k).			x(k\|k)
	Таким образом, чтобы решить поставленную задачу, достаточно найти оценки					x(k\|k)
è	x(k + 1\|k).

Линеаризуем задачу. Разложим функции f(xk), b(xk) è h(xk+1), B(xk+1) в ряды Тейло ра соответственно в окрестностях точек xnk è xk+1 с точностью до членов первого порядка

малости относительно

xk è

xk+1. Соотношения (10.1) и (10.2) предстанут в следующем

âèäå:

xk+1

= f(xkn) +

∂f

+ b(xkn)wk +

∂b

xk wk + o(Δxk)! ;

(10.13)

∂x

x=xn

∂x

x=xn

∂f

∂B

+ o(Δxk+1)! .

yk+1

= h(xk+1) +

xk+1 + B(xk+1)vk+1 +

xk+1 vk+1

∂x

x=xn

∂x

x=xn

k+1

(10.14)

Вычитая из соотношения (10.13) соотношение (10.4) (вид опорной траектории) и пренебре

предложения в условиях задачи			∂b			xk wk + o(Δxk)
гая слагаемым в круглых скобках,			∂x		x=xn	xk wk + o(Δxk)		см. аппроксимирующие
					k
		íàéä¼ì:
x		=		∂x x=xkn		x	+ b(xn)w .	(10.15)
x		=		∂f		x	+ b(xn)w .	(10.15)
	k+1					k	k k

Учитывая (10.10) введ¼нные обозначения для					xk,	xk+1,		yk+1
записать:					∂x	x=xk+1	x	k+1	k+1
емым в круглых скобках в соотношении (10.14),					∂B	n	x		v
		∂h	x=xkn			n
		∂x	x=xkn
	yk+1 =			xk+1 + B(xk+!)vk+1 .

и пренебрегая слага

+ o(Δxk+1) можно

(10.16)

Таким образом, мы получили линейные модели ((10.15) (10.16)) для оценивания вари ации вектора состояния xk относительно номинальной траектории по отклонению yk полученных измерений относительно номинальных. [Функции b(xk) è B(xk) вычисляя в точке номинальной траектории].

Для полученных линейных моделей может быть примен¼н линейный фильтр Калмана. Заметим при этом, что

xt è xt+Δt

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

Тогда из соотношений стандартного линейного фильтра Калмана с уч¼том (10.10) непосред ственно следует справедливость (10.5) (10.9), ч. т. д.

Что можно сказать о полученном алгоритме? Преимущество линеаризованного филь тра Калмана состоит в том, что коэффициенты усиления не зависят от состояния и могут быть вычислены заранее на основе номинального решения (опорной траектории). Однако имеется недостаток, заключающийся в том, что течением времени оценка может стать значительно отличающейся от опорной и тогда становятся существенными нелинейности.

При этом поскольку опорная траектория при данном подходе строится только на основе априорной информации (по заданному xn0 строится xnt è xnt +Δt), то с течением времени воз

растание ошибок прогноза становится практически неизбежным и тем самым нарушаются допустимые условия применимости рядов Тейлора для разложения нелинейных функций моделей системы и измерений.

Исправить эту ситуацию можно двумя путями:

использование измерительной информации для получения оценки xˆt на момент вре ìåíè t = tk;

уменьшением интервала прогноза с tk − t0 до минимального значения, т. е. экстрапо лируется значение xˆt+Δt по начальным условиям xˆt.

При правильной работе алгоритма оценивания значения xˆt è xˆt+Δt будут ближе к истинным , чем прогнозные значения xnt è xnt+Δt. Построив указанным способом новые опор ные траектории, расширяем класс опорных траекторий , введ¼нных ранее. Алгоритмом

оценивания, построенные с использованием процедуры линеаризации нелинейных функ ций моделей системы и измерений в точках расширенного класса опорных траекторий , будем называть расширенными линеаризованными алгоритмами оценивания .

Расширенный дискретный фильтр

Äàíî:

1. Модель системы:

xk+1 = f(xk) + Gk wk ;

(10.17)

2. Модель дискретных измерений:

yk+1 = h(xk+1) + vk+1 ;

(10.18)

3.Априорная информация вида (10.3);

4.Выборка измерений: Y1k = {ys : s = 1, . . . , k};

5.Аппроксимирующие предложения: функции f(xk) è h(xk+1) раскладываются в ря

бесконечно малая величина относительно своего аргумента; пренебречь значениями статистическими моментами третьего и более высокого порядков.

Доказать:

1. Алгоритм экстраполяции значений

x(k + 1|k) = E(xk+1|Y1k) è P (k + 1|k) = cov(xk+1, xk+1|Y1k)

Мальцева Н. В.

Рекуррентная и адаптивная фильтрация

имеет вид:

x(k + 1|k) = f(x(k|k)) ;

+ Gk Qk GkT ;

(10.19)

P (k + 1|k) = ∂x x=x(k k) · P (k|k)

∂x

(10.20)

∂f

x=x(k k)

∂f

2. Алгоритм фильтрации значений

x(k + 1\|k + 1) = E(xk+1\|Y1k+1)			è	P (k + 1\|k + 1) = cov(xk+1, xk+1\|Y1k+1)
зада¼тся рекуррентными соотношениями:
x(k + 1\|k + 1) = x(k + 1\|k) + Kk+1[yk+1 − h(x(k + 1\|k))] ;						(10.21)
∂h		x=x(k+1 k)! · P (k + 1\|k) ;				(10.22)
P (k + 1\|k + 1) = I − Kk+1 ∂x		x=x(k+1 k)! · P (k + 1\|k) ;				(10.22)
				\|
				\|
		T
	∂h				×
Kk+1 = P (k + 1\|k) ∂x					×

x=x(k+1|k)

∂x x=x(k+1 k) · P (k + 1|k) ·

∂x

+ Rk+1

(10.23)

∂h

x=x(k+1

−1

Доказательство :

Данную задачу можно рассматривать как частный случай предыдущей. После полу чения выборки измерений {Y1k} два значения оцениваемого вектора x, соответствующие

последовательным моментам времени tk è tk+1 и принадлежащего опорной траектории, могут быть выбраны так, что xnk = x(k|k) è xnk+1 = x(k + 1|k).

Кроме того, сопоставляя условие задач, видим, что G(xk) = Gk и не зависят от оценива емого процесса {xk}, (в предыдущей задаче G(xk) = b(xk)), à B(xk+1) = E, поэтому из соот ношений (10.5) (10.9), как частный случай, следует справедливость равентсв (10.19) (10.23).

Отметим следующую особенность расширенного фильтра Калмана и всех его возмож ных модификаций: фильтр вычисляет искомые величины, минимизируя уравнения относи тельно последней оценки = и коэффициент усиления, и ковариационные матрицы зави

сят от текущей оценки и могут быть вычислены только в реальном масштабе времени. Ещ¼ большее возможное повышение точности оценивания может быть достигнуто за

сч¼т применения итерационного расширенного фильтра Калмана (естественно, за сч¼т воз растания объ¼ма вычислений). Итерационный расширенный фильтр Калмана способствует

уменьшению влияния нелинейностей в измерениях за сч¼т итерационного уточнения оцен ки при любом измерении до тех пор, пока изменение оценки не станет малым.

Формулы для такого фильтра выглядят следующим образом.

Обозначим :

(·)k|i значение величины (·) на k-ом шаге измерений после i-итераций;

(·)−k прогнозируемые значения величины (·) íà k-ûé шаг измерения; (·)+k оценка после k-шагов измерений.

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете Рекурсивная и адаптивная фильтрация

#
01.05.2014675.33 Кб85Конспект по фильтрации.pdf
#
01.05.20141.06 Mб28Лабораторная работа.doc