Задания для контрольной работы №2.

1. Задачи целочисленного линейного программирования.

1-14. Найти полностью целочисленное решение следующих задач, сопровождая (где это возможно) решение графической иллюстрацией (предполагается, что все ).

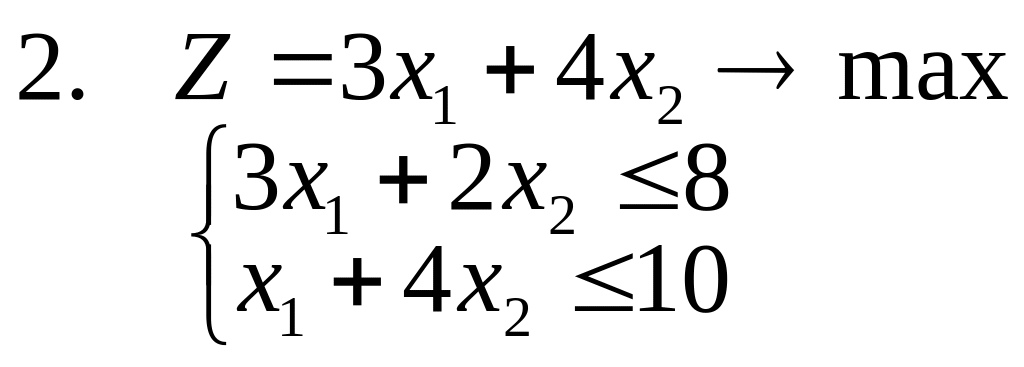
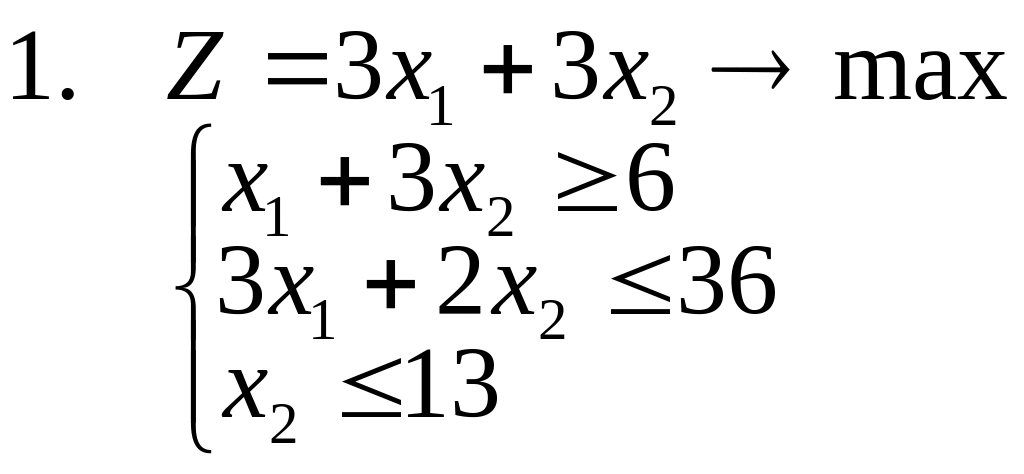
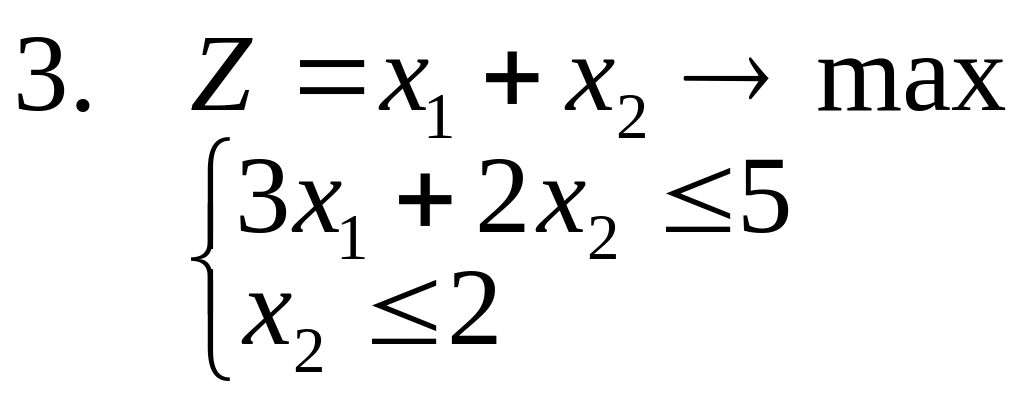
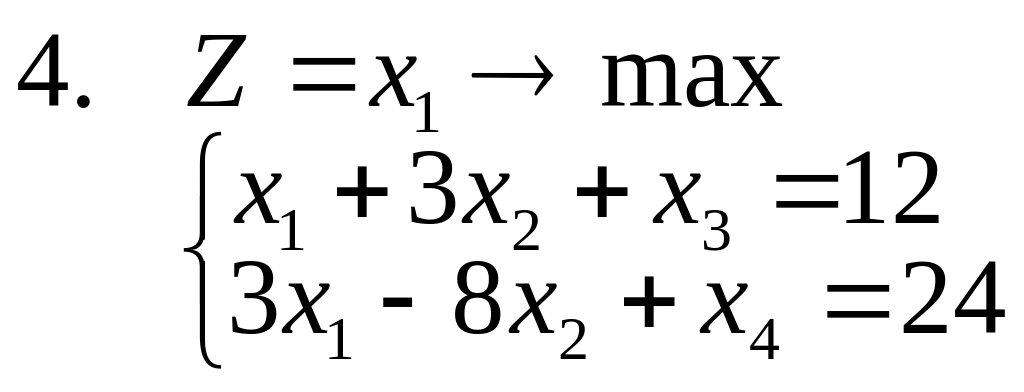
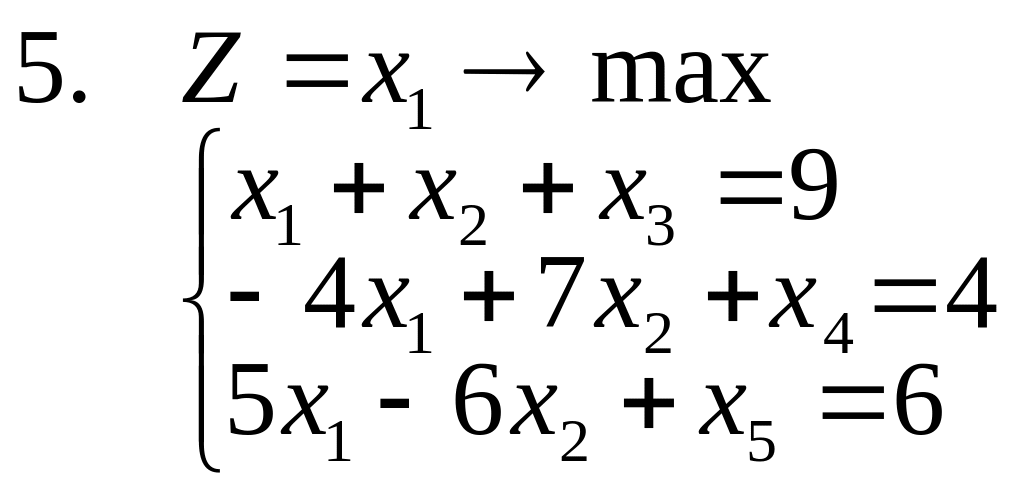
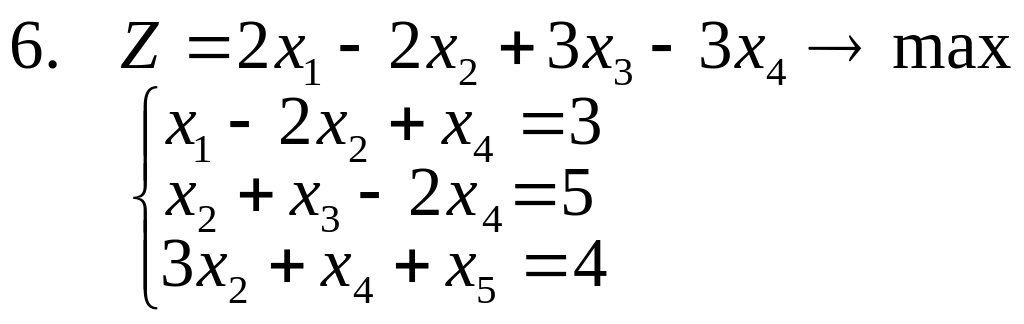
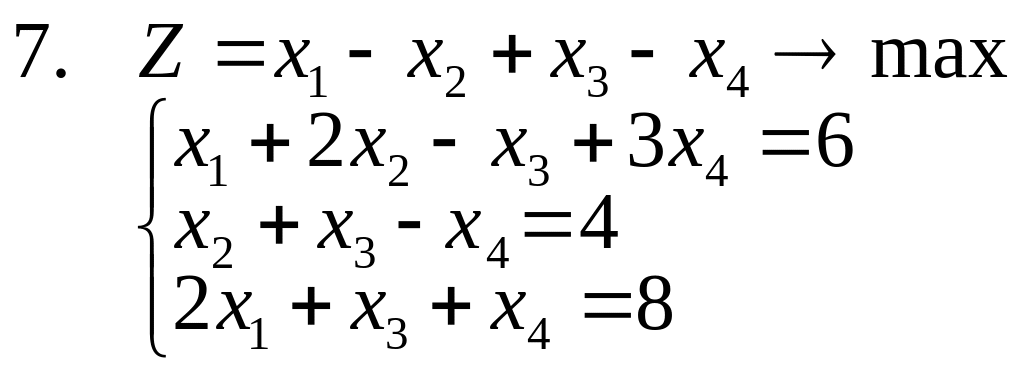
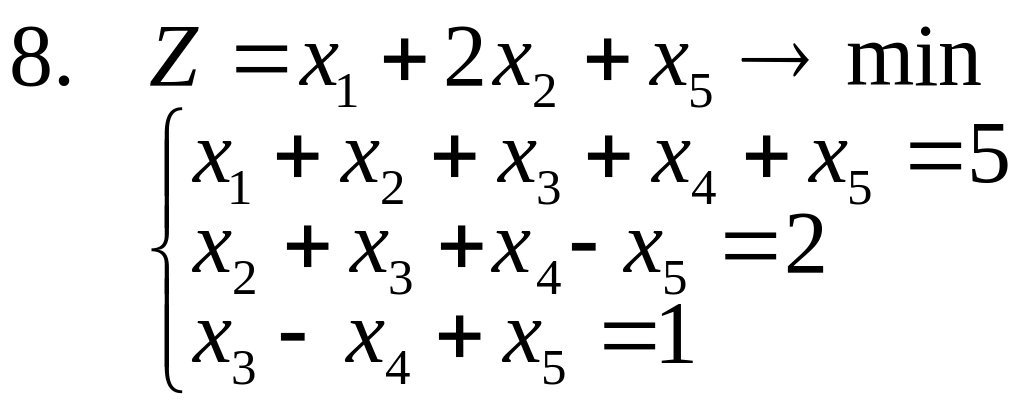
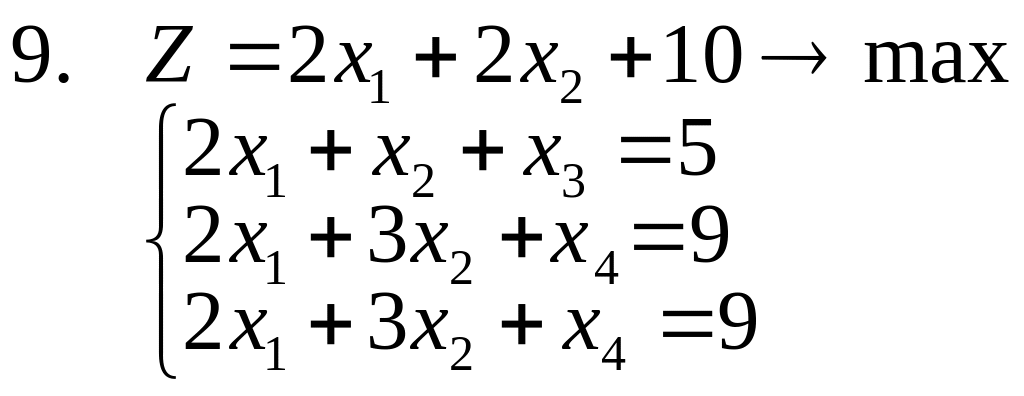
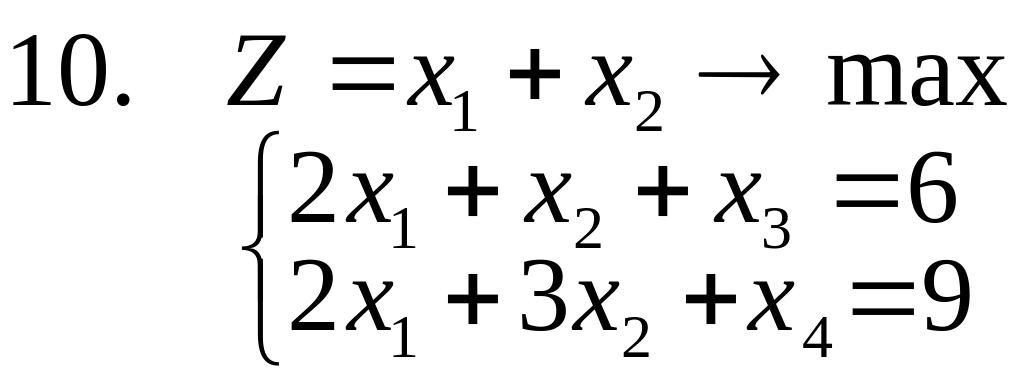
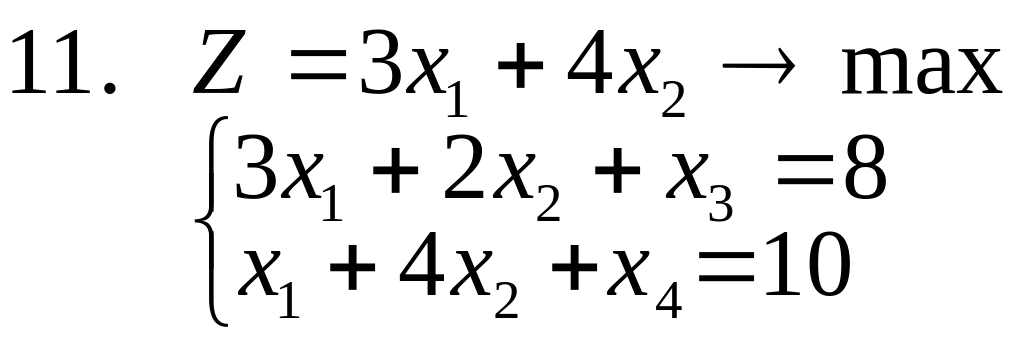
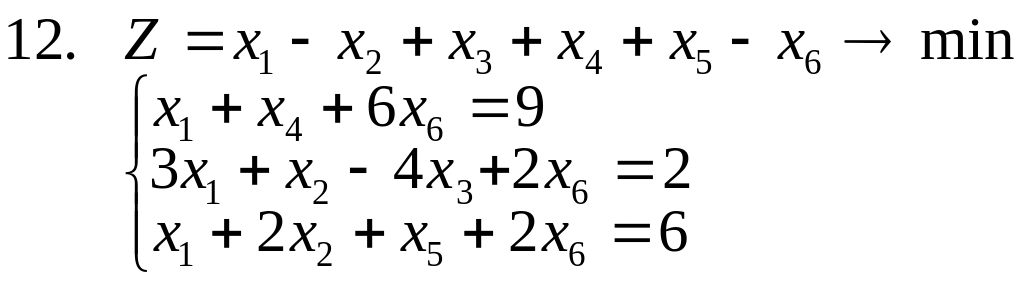
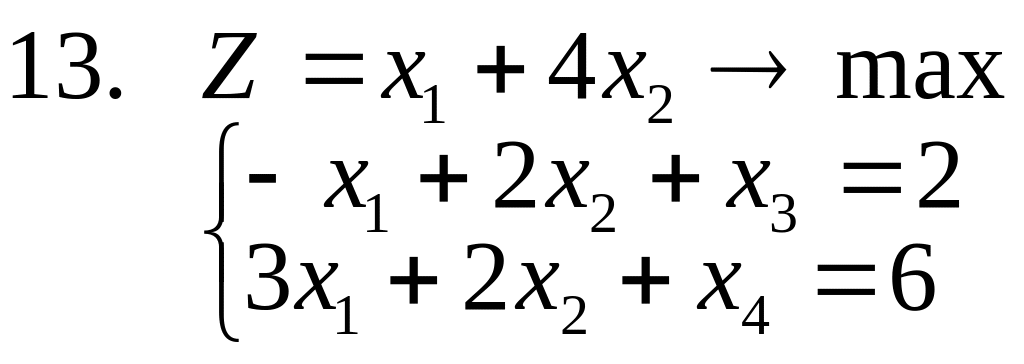
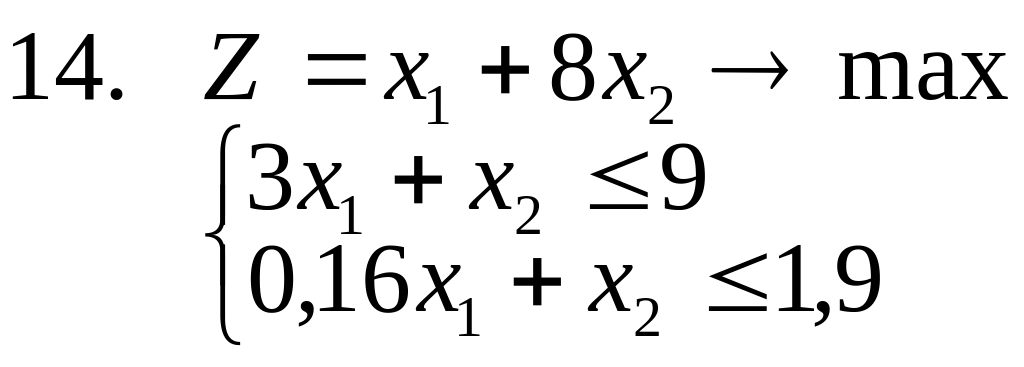
15. Решить задачи 1-3, используя метод отсекающих плоскостей. Дать геометрическую интерпретацию решения.

16. Доказать, что дополнительное ограничение вида , где суммирование распространяется на все свободные переменные в оптимальном нецелочисленном решении задачи , является «сечением» для построения задачи .

17. Привести к целочисленной задачу максимизации в области, изображенной на рисунке 12.

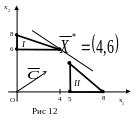
18. Привести к задаче целочисленного программирования следующую задачу: максимизировать при условиях:

а) и либо , либо ;

б) и либо , либо .

19. Дана полностью целочисленная задача:

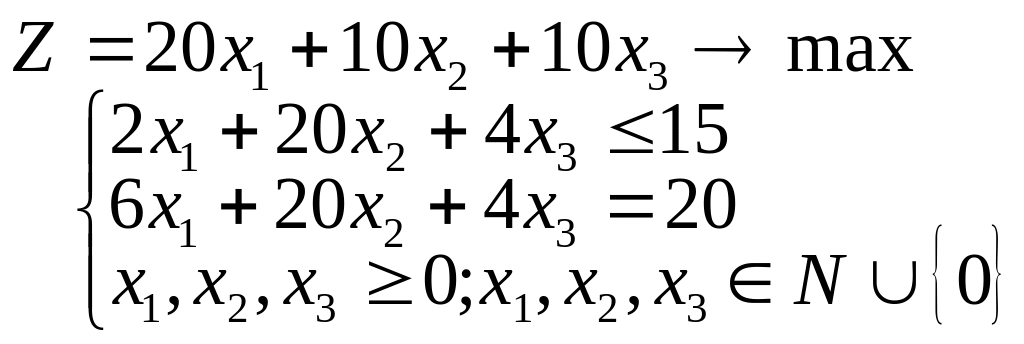
Докажите, что решение этой задачи нельзя получить методом округления.

20. На примере полностью целочисленной задачи

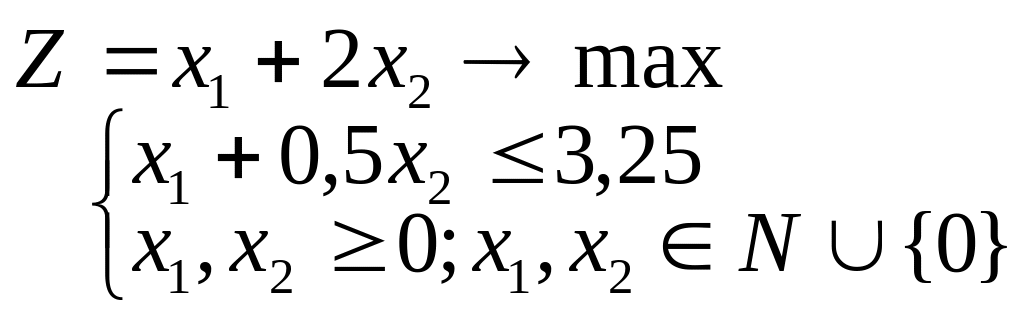
Покажите, что метод Гомори для полностью целочисленной задачи не приводит к оптимальному решению, если не выполняется требование целочисленности значений ее параметров. Преобразуйте рассматриваемую задачу и методом Гомори найдите ее оптимальное решение.

21-26. Решить следующие частично целочисленные задачи (предполагается, что все ).

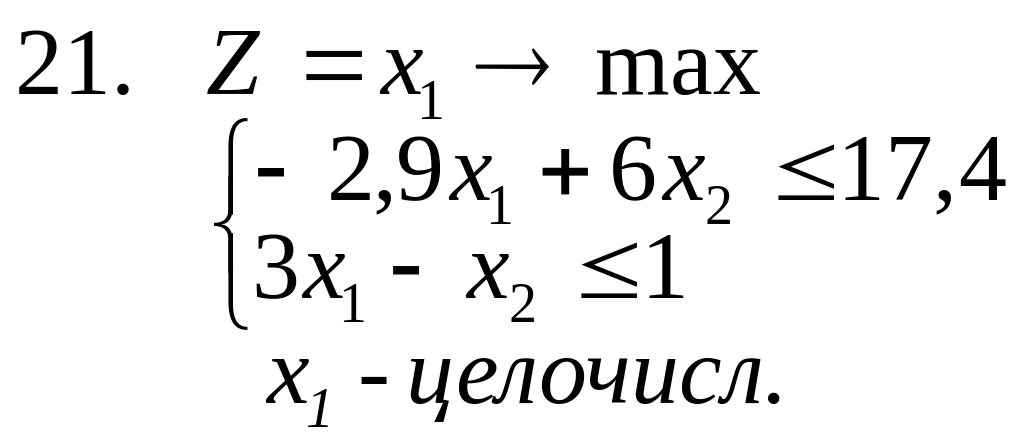
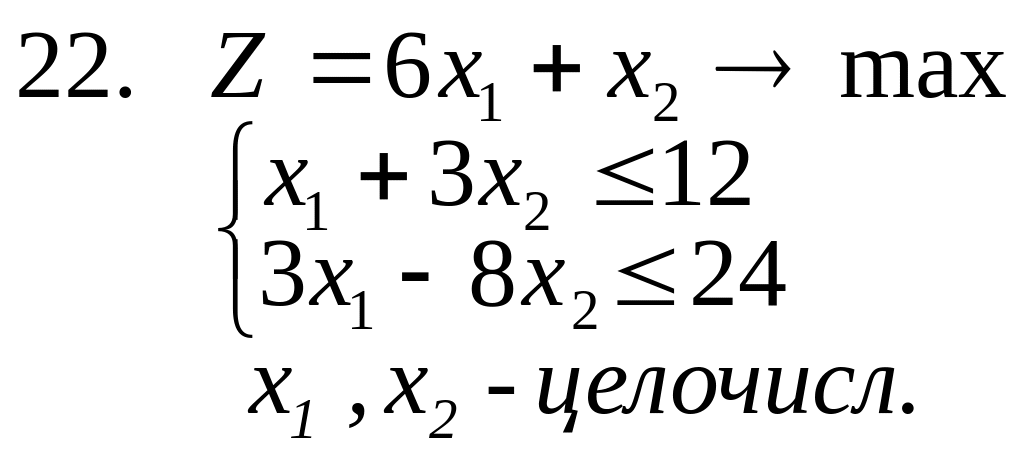
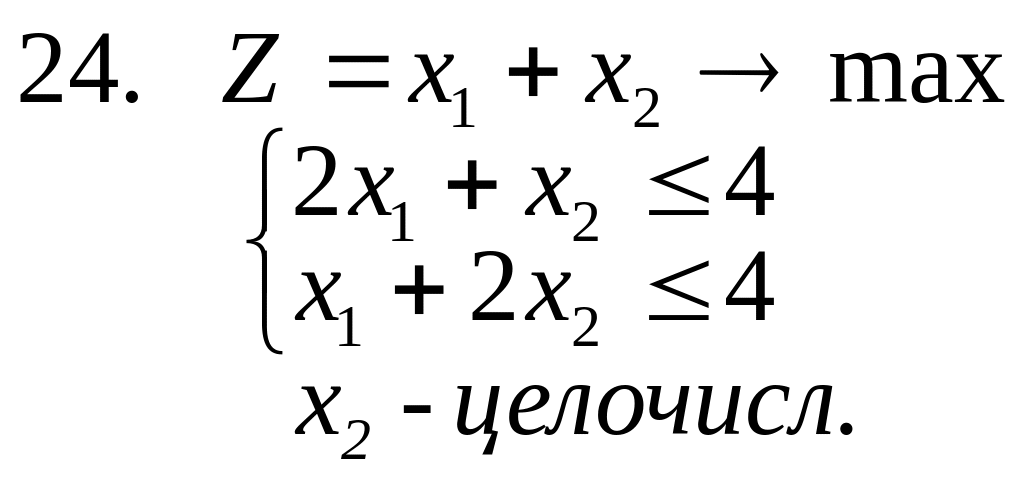
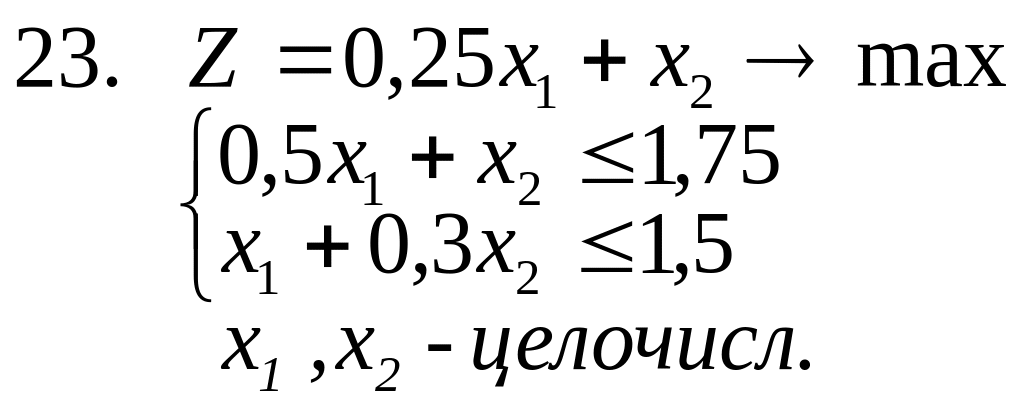
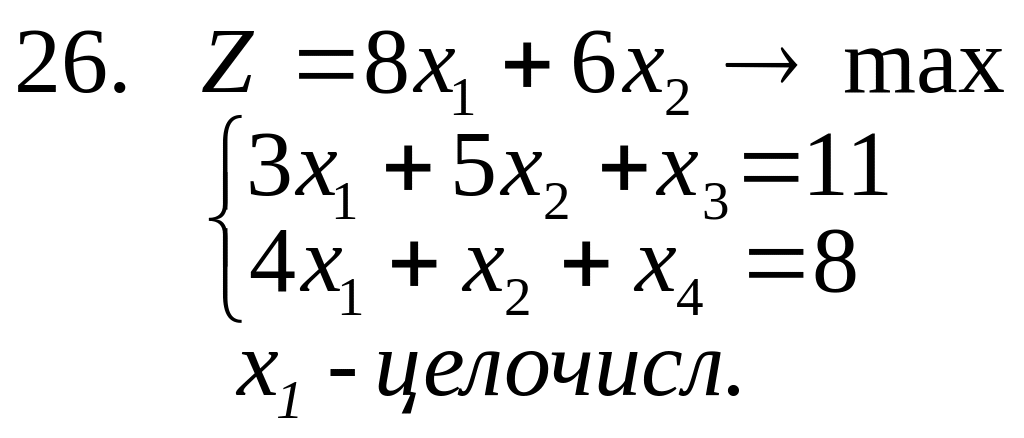
27. Преобразовать в полностью целочисленные задачи 21 и 24 и сравнить их решение с предыдущим.

2. Задачи с неделимостью, решаемые методами целочисленного линейного программирования.

28. Составить модель задачи по определению оптимального плана производства n типов машин при заданных объемах ресурсов, нормах расхода i – го ресурса на производство одной k- той машины и величинах прибыли при реализации одной машины k- го типа. Предполагается, что к концу планируемого периода не должно быть незавершенного производства.

29. Имеется m типов машин (i = 1,…, m) и n видов работ , подлежащих выполнению в объемах . Задана матрица , где - производительность i - той машины на k - й работе, матрица , где - себестоимость выполнения единицы k – й работы машиной i – ого типа, и стоимость одной машины i – ого типа.

Составить математическую модель задачи по определению оптимального машинного парка (т.е. количество машин каждого типа) и оптимального его распределения по указанным работам из условия минимизации суммарной стоимости (машинного парка и производных работ).

Указание: Ввести два вида переменных: - общее число машин i – го типа и - количество машин i – го типа, используемых на k – й работе; последние могут и не быть целочисленными, если производительность машин не кратна объему работы .

30. Имеются суда m типов в количествах , на каждом из которых имеются n грузовых емкостей (k = 1,2,…,n) с грузоподъемностью (некоторые могут быть равны нулю). Подлежат перевозке p видов грузов в количестве . Составить математическую модель задачи по выбору оптимального состава судов, если затраты по эксплуатации одного i – го типа равны .

31. Имеется n маршрутов, по каждому из которых необходимо совершить (k = 1,…,n) и m типов автомашин, каждая из которых может быть использована в течение ч (i = 1,…,m). На выполнение i –й машиной рейса по k – му маршруту требуется ч при затратах руб. Составить модель задачи оптимального распределения машин по маршрутам.

32. Требуется распилить a бревен, длиной каждое в 10 м, на брусьях трех размеров: 3,5; 4,5 и 5 м, которые должны быть изготовлены в ассортименте 2:1:1. Составить модель для определения оптимального плана распила из условия максимального использования каждого бревна.

33. (Задача об оптимальном назначении.) Имеется n работ (k – 1,2,…,n) и m механизмов (i – 1,…,m), способных выполнить эти работы. Задана матрица , элементы которой характеризуют эффективность выполнения i – м механизмом k – й работы. При этом в качестве дополнительного условия принимается, что каждый механизм может быть использован только на одной работе и каждая работа может выполняться только одним механизмом. Составить модель задачи оптимального распределения механизмом.