Косозубые цилиндрические эвольвентные передачи и особенности их расчета.

Косозубыми называются цилиндрические эвольвентные зубчатые передачи, боковая поверхность зуба которой образована наклонной прямой лежащей в производящей плоскости и образующей с линией касания с основным цилиндром угол .

Переходя к изучению косозубых передач, отметим, что косые зубья располагаются на цилиндрах обоих колес по винтовым линиям. Если цилинд­ры развернуть на плоскость, то косые зубья (на развертке) окажутся расположенными по наклонным параллельным прямым. Так же будут расположены и косые зубья рейки.

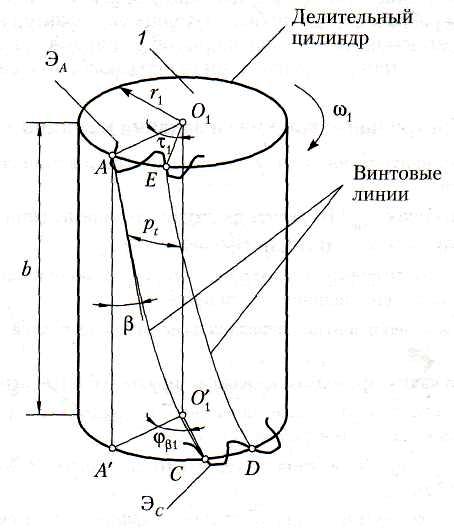
Косозубые колеса, как и прямозубые, изготовляются спо­собом обкатки, в основу которого положен процесс станочного зацепления. Для нарезания применяет­ся тот же стандартный инструмент, но устанавливается он на станке наклонно, под углом . Поэтому про­изводящая зубчатая поверхность, которую в своем техно­логическом движении 3 описывают режущие кромки инст­румента гребенки, тоже будет наклонной. На рис. производящая поверхность показана схематично, в виде на­клонно проецирующих линий. А так как эта поверхность (если ее мысленно сделать материальной) образует зубья воображаемой производящей рейки, то, следовательно, зубья рейки получатся косыми. Наглядно процесс обкатки можно представить себе как качение изготовляемого колеса по производящей рейке, имеющей косые зубья, накло­ненные под углом .

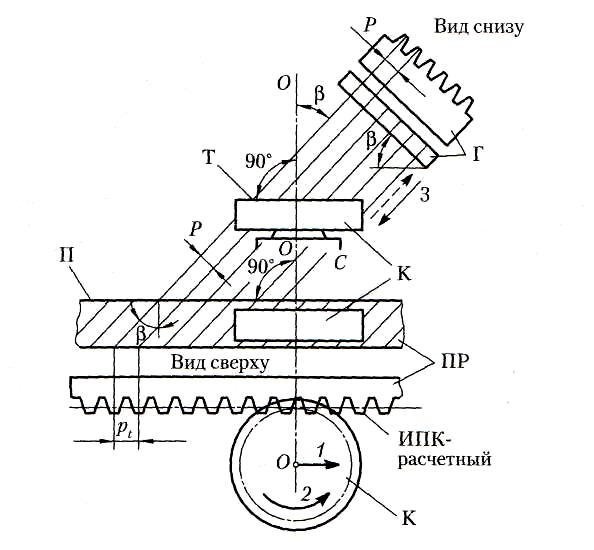
Такой же наклон получат зубья изготовляемого коле­са на его станочно-начальном цилиндре. А так как в реечном станочном зацеплении делительный цилиндр совпа­дает со станочно-начальным, то именно на делительном цилиндре зубья получатся расположенными под углом , на который наклонен инструмент на станке.

Движения обка­та 1 и 2 при изготовлении как прямозубых, так и косозубых колес одинаковы. Отсюда следует весьма важный вывод: все принципиальные положения, касающиеся станочного зацепления прямозубого колеса с прямозубой производя­щей рейкой, справедливы также для ста­ночного зацепления косозубого колеса с косозубой произ­водящей рейкой.

Вместе с тем процесс изготовления косозубых колес имеет и свои особенности, вытекающие из того, что инструмент установлен на станке наклонно. Определим, каким бу­дет в этих новых условиях исходный производящий контур (ИПК), вступающий в станочное зацепление с профилем нарезаемых зубьев. Для этого рассечем наклонную зубчатую производящую поверхность плоскостью П, перпендикуляр­ной оси 00 колеса; в сечении получим искомый ИПК.

Нетрудно заметить, что благодаря наклону инструмента параметры полученного ИПК будут отличаться от пара­метров стандартного ИПК, который образуется при пере­сечении производящей поверхности плоскостью, ей пер­пендикулярной. Например, шаг нового ИПК составит

,

где — шаг стандартного ИПК. Поэтому

,

где — стандартный модуль инструмента.

Чтобы в дальнейшем отличать стандартные параметры от расчетных, будем присваивать пос­ледним значок . Следовательно, особенность станочного зацепления при изготовлении косозубых колес состоит в том, что благодаря наклонной установке инстру­мента ИПК не является больше стандартным, а становится расчетным.

Здесь надо сделать принципиально важное добавление. Расчетный реечный ИПК, как и стандартный, имеет прямолинейные, т.е. эвольвентные, кромки. Поэтому в торцевой плоскости Т косозубого колеса, как и в любой, ей параллельной (П), зубья при изготовлении получают эвольвентный профиль. Но именно в этих плос­костях, перпендикулярных осям вращения колес проекти­руемой передачи, и происходит сам процесс зацепления профилей ее зубьев. Значит, косозубая цилиндрическая передача является эвольвентной передачей. Отсюда следует еще один важный вывод: все теоретические положения и зависимости, полученные ранее для прямозубой эвольвен­тной передачи, полностью справедливы и для косозубой, но сформированной на базе расчетного ИПК. Поэтому ма­тематическая структура всех ранее составленных формул сохранится, но написание их будет иметь ту особенность, что всюду вместо стандартных параметров в них надо подставлять расчетные параметры , зави­сящие от угла . Например:

При нарезании косозубого колеса инструментальная рейка поворачивается на угол , при этом стандартный исходный производящий контур располагается в нормальной плоскости, а в расчетной торцевой плоскости образуется другой, торцевой контур, параметры которого укажем без вывода:

; ; ; ; ; .