4.7 Выводы

1) В настоящее время существует большое количество задач механики, решаемых с применением конечно-элементных комплексов;

2) В силу сложности восприятия вариационных формулировок уравнений метода конечных элементов обычно используется прямой метод формулировки, позволяющий заменить интегральные и дифференциальные уравнения на алгебраические;

3) На сегодняшний момент возможно провести успешный инженерный анализ конструкции даже с применением САПР среднего уровня, а также объяснить его с помощью общеизвестных формул, увеличив прозрачность вычислений;

4) Использование программных комплексов моделирования и инженерного анализа конструкций несмотря на внешнюю простоту требует от пользователя ответственного подхода и знаний в различных отраслях науки – математики, моделирования, информатики и более узких дисциплин; в противном случае полученные результаты расчета могут оказать неприемлемыми;

5) Поиск литературных источников по описанию методик расчета в современных программных комплексах довольно затруднен, поэтому кажется целесообразным издание литературы, освещающей и обосновывающей различные современные методики компьютерного расчета, что может облегчить освоение программных комплексов и трактовку результатов анализа.

5 Исследование напряженно-деформированного состояния рамы с использованием компьютерного моделирования

5.1 Расчет на изгиб

С использованием балочной конечно-элементной модели в SolidWorks был выполнен расчет рамы на изгиб. Следует отметить, что здесь и далее по умолчанию будут описываться расчетные схемы нагружения для балочной модели. С учетом рекомендаций [15, 39, 40] и сведений об автомобиле [26] была выбрана схема нагружения:

1) Статические граничные условия: в местах крепления задней подвески к раме (2 точки на каждом лонжероне) ограничено перемещение по трем степеням свободы (вращение не ограничено), а в местах крепления передней подвески ограничено перемещение в вертикальном направлении (2 точки на каждом лонжероне).

2) Кинематические граничные условия: обобщенный вес двигателя и коробки передач (709 Н) приложен к соответствующим несущим поперечинам, обобщенный вес кабины, водителя и пассажира в кабине (1150 Н) приложен к передней и средней части лонжеронов, обобщенный вес кузова и пассажиров (21200 Н) приложен к средней и задней части лонжеронов.

3) Крепления поперечин и лонжеронов подробно не моделировались, а геометрия скрепленных элементов рамы принималась связанной.

Несмотря на то, что модель симметрична, для лучшего восприятия она рассчитывалась целиком.

Карта напряжений, соответствующая совместному действию осевых и изгибающих напряжений, приведена на рис. 24. Наибольшее напряжение для балочной модели составило 101,6 МПа и было достигнуто в средней части рамы. Для автомобилей-внедорожников динамический коэффициент, позволяющий учитывать динамическое нагружение в процессе эксплуатации находится в диапазоне значений 3,0-4,0 [15-97]. А так как предел упругости материала лонжерона – стали 15ГЮТ составляет 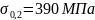, то использование динамического коэффициента больше значения 3,8 может привести к появлению пластических деформаций, что недопустимо [37].

В связи с этим встает вопрос о необходимости увеличения прочности рамы, особенно в средней ее части, на лонжеронах.

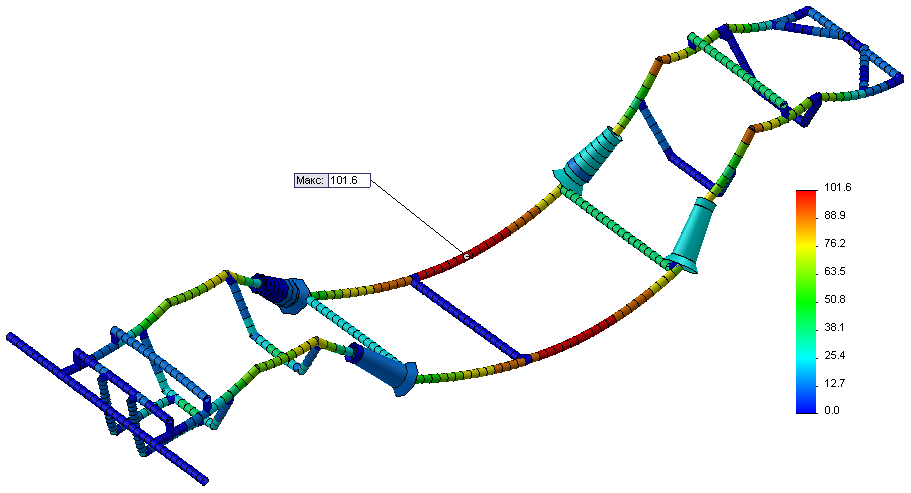
Рис. 28 – Карта осевых и изгибающих напряжений балочной модели в расчете на изгиб (SolidWorks)

Наиболее велик вклад в напряженно-деформированное состояние именно изгибающих напряжений, как это наглядно проиллюстрировано на соответствующей карте напряжений (рис. 25). Наибольшее отрицательное напряжение -96 МПа было достигнуто в средней части рамы. Наибольшие осевые напряжения были выявлены в поперечинах, к которым крепится двигатель, но имеют незначительные величины.

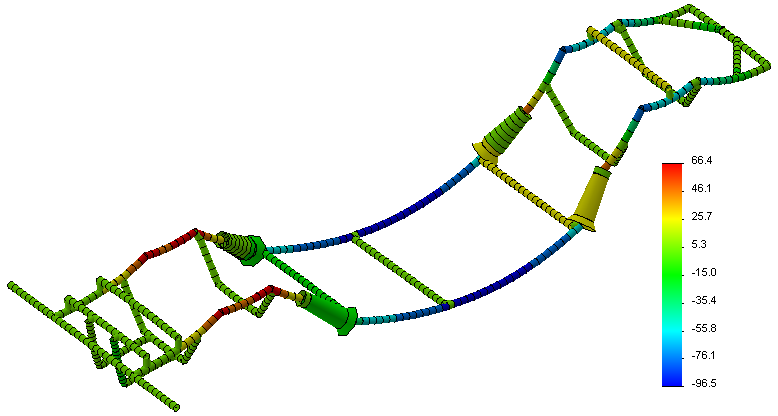
Рис. 29 – Карта вертикальных изгибающих напряжений балочной модели в испытании на изгиб (SolidWorks)

При проведении расчета на изгиб с использованием оболочечной модели была избрана такая подобная схема нагружения, что и для балочной модели. Отличие заключается в том, что вместо точек приложения статических граничных условий использовались грани, что способствует более верным результатам и лучше соответствует действительности.

Карта эквивалентных напряжений по Мизесу для оболочечной модели изображена на рис. 26. Следует отметить, что красные области наибольших напряжений (186 МПа) на рис. 26 расположены около статических граничных условий, которые в SolidWorks не удалось исключить в силу отсутствия инструментов стабилизации модели и провала использования податливых граничных условий. Также красные области расположены в местах перехода от крайних частей рамы к средней, что связано с концентрацией напряжений у кромок и вершин и также не может быть устранено в силу особенностей анализа - только простая геометрия может использоваться в SolidWorks для создания оболочечных конечно-элементных моделей. Однако, абстрагируясь от вышеуказанных особенностей, необходимо обратить внимание, что наибольшее напряжение возникает в средней части рамы, причем достигает наибольшего значения в 99,7 МПа около VI поперечины, что вполне согласует с результатом расчета балочной модели. Это напряжение и следует принять максимальным на этой карте.

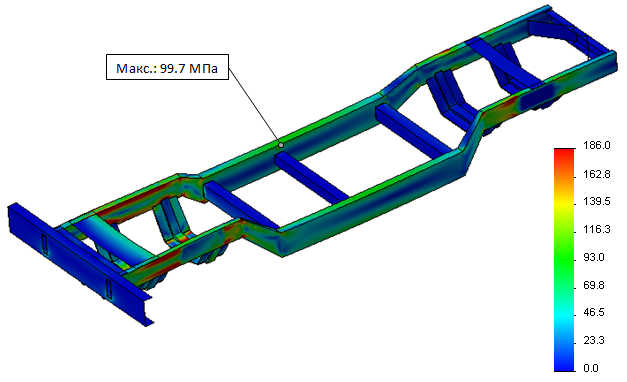
Рис. 30 – Карта эквивалентных напряжений оболочечной модели в расчете на изгиб (SolidWorks)

Расчет с использованием упрощенной сплошнотельной модели дал результаты, аналогичные результатам расчета оболочечной модели, однако максимальное значение в средней части рамы составило 111,7 МПа. Здесь и ниже карты напряжений, полученные в результате расчета упрощенной сплошнотельной модели приводиться не будут, так как практически полностью соответствуют картам напряжений, полученным в результате расчета оболочечных моделей.