
- •1 Обзор программных средств моделирования и расчета, компьютерных исследований конструкций автомобилей
- •1.1 Обзор программных комплексов, использующих методы дискретизации
- •1.2 Обзор программных комплексов для решения задач динамики движения
- •1.3 Обзор инженерно-проектных работ и научных исследований в области моделирования и конечно-элементного расчета конструкций транспортных средств
- •2 Описание конструкции рамы и моделей
- •2.1 Описание некоторых конструктивных особенностей лонжеронных автомобильных рам
- •2.2 Описание конструкции исследуемой рамы и моделей
- •2.2 Выводы
- •3 Описание и обоснование распространенных методик расчета рам
- •3.1 Статические расчеты
- •3.2 Выводы
- •4 Описание методики расчетов в конечно-элементных комплексах
- •4.1 Матричная формулировка основных уравнений мкэ для решения задач статики
- •4.2 Особенности реализации метода конечных элементов в SolidWorks и Abaqus
- •4.3 Формирование уравнений движения и описание собственных форм и частот конструкции в методе конечных элементов
- •4.4 Решатели в SolidWorks и Abaqus
- •4.5 Особенности описания движения твердых тел в программном комплексе фрунд
- •4.5 Особенности расчета ударного воздействия
- •4.6 Определение усталостного срока службы
- •4.7 Выводы
- •5 Исследование напряженно-деформированного состояния рамы с использованием компьютерного моделирования
- •5.1 Расчет на изгиб
- •5.2 Расчет кососимметричного нагружения
- •5.3 Расчет кручения
- •5.4 Расчет бокового удара
- •5.5 Расчет на продольное нагружение
- •5.6 Расчет собственных форм и частот колебаний
- •5.7 Расчет столкновения с препятствием
- •5.8 Расчет усталостного срока службы
- •5.9 Выводы, результаты, предложения совершенствования
4.4 Решатели в SolidWorks и Abaqus
В SolidWorks доступны прямой и итерационный решатели.
Итерационный
решатель обладает большей скоростью
вычислений (особенно с числом узлов
более
 ),
позволяет решать нелинейные задачи.
Согласно МКЭ нелинейные проблемы
формулируются системой нелинейных
алгебраических уравнений вида:
),
позволяет решать нелинейные задачи.
Согласно МКЭ нелинейные проблемы
формулируются системой нелинейных
алгебраических уравнений вида:
 ,
(49)
,
(49)
где
- неизвестные перемещения;
 - общие внешние воздействия в узлах.
Задача состоит в определении неизвестных
,
зависящих от
.
- общие внешние воздействия в узлах.
Задача состоит в определении неизвестных
,
зависящих от
.
В итерационных методах аппроксимация решения происходит при общем нагружении, без разбиения нагрузки на части, имеющей место быть в инкрементальных методах. В каждом последующем шаге (итерации) предполагается, что матрица жесткости постоянна. В связи с этим появляются неуравновешенные (остаточные) нагружения, отступления от равновесия. После каждой итерации определяют неуравновешенные нагружения и учитывают при следующей итерации. Действия повторяют, пока все условия равновесия не будут удовлетворены с необходимой точностью.
В итерационном решателе SolidWorks и Abaqus реализованы обычный и модифицированный методы Ньютона-Рафсона для корректировки параметров, описывающих состояние системы [50].
Если
 - приближенное решение системы нелинейных
уравнений, то его улучшают, если
вектор-функция остаточных сил
раскладывается в ряд Тейлора вблизи
- приближенное решение системы нелинейных
уравнений, то его улучшают, если
вектор-функция остаточных сил
раскладывается в ряд Тейлора вблизи
 :
:
 ,
(50)
,
(50)
где
- функция остаточных сил,
 - инкрементное (приращенное) перемещение.
- инкрементное (приращенное) перемещение.
Учитывается условие, что исправленное решение отвечает условиям равновесия, т.е.:
 .
(51)
.
(51)
Тогда справедливо:
 ;
(52)
;
(52)
где
 - тангенциальная матрица жесткости.
- тангенциальная матрица жесткости.
После определения
 определяют
из выражения:
определяют
из выражения:
 .
(53)
.
(53)
Итерационный метод
Ньютона-Рафсона ведет к быстрой сходимости
решения и обладает высокой устойчивостью.
Но при каждом повторном шаге необходимо
вычислять матрицу жесткости системы и
решать новую систему уравнений, что
увеличивает его вычислительную стоимость.
Для устранения этого недостатка
используется модифицированный метод
Ньютона-Рафсона, предполагающего, что
матрица
 в ходе итерации не меняется [3]:
в ходе итерации не меняется [3]:
 ,
(54)
,
(54)
где
 – тангенциальная матрица
– тангенциальная матрица
 итерации;
итерации;
 - тангенциальная
матрица нулевой итерации.
- тангенциальная
матрица нулевой итерации.
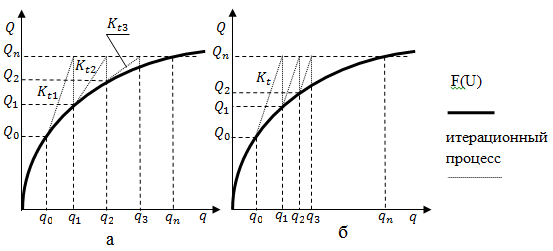
Рис. 27 – Пояснительные иллюстрации к итерационному методу Ньютона-Рафсона: а – обычный метод; б – модифицированный
Порядок итерации
формально остается прежним с той
разницей, что вместо
применяется
.
Различие состоит в том, что в этом случае
необходимо также на первом шаге решить
систему уравнений, а в каждой следующей
итерации выполнять поправку правой
части уравнения с
 :
:
 .
(55)
.
(55)
Модифицированный метод Ньютона-Рафсона значительно экономичнее обычного несмотря на более медленную сходимость, потому чаще используется [50].
