Лекция 6 (продолжение). Примеры решения на плоский изгиб и задачи для самостоятельного решения

 

Определение перемещений и проверка жесткости балок при изгибе

При расчете строительных и машиностроительных конструкций на жесткость (в большинстве случаев по прогибам, по углам поворота) должно соблюдаться условие

т.е. относительный прогиб f/l, подсчитанный при действии нормативных нагрузок, не должен превышать установленный нормами предельный прогиб 1/n_o для данного вида конструкции.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений:

.

Допускаемый угол поворота берется из соответствующих справочников. В среднем составляет 0,001 рад.

 

Пример 1.

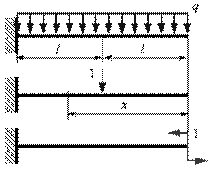
Для консольной балки с сосредоточенной парой M_o на свободном конце найти аналитические выражения для прогибов и углов поворота.

 

Решение.

По дифференциальным уравнениям имеем

.

В заделке прогиб y(0) и угол поворота сечения равны нулю. Эти граничные условия будут удовлетворены, если C₁=0 и C₂=0. Следовательно, балка изогнется по дуге параболы:

.

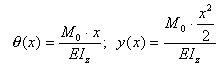На этом примере наглядно проявляется приближенный характер уравнения, так как при постоянном изгибающем моменте согласно равенству

балка должна изгибаться по дуге окружности радиуса . Однако в пределах длины балки указанные дуги окружности и параболы практически совпадают.

 

Пример 2.

Для консольной балки с сосредоточенной силой P на свободном конце найти аналитические выражения для прогибов и углов поворота.

Решение.

Реактивная сила и момент в заделке равны R=P, M_R=Pl. В произвольном сечении на расстоянии x от заделки имеем

.

В заделке прогиб y(0) и угол поворота сечения равны нулю. Эти граничные условия будут удовлетворены, если C₁=0 и C₂=0. Окончательно, имеем

.

Максимальные прогиб и угол поворота будут на правом свободном конце балки:

.

Знак минус в формулах для прогиба и угла поворота означает, что прогиб конца консольной балки направлен вниз, а поворот концевого сечения – по часовой стрелке.

 

Пример 3.

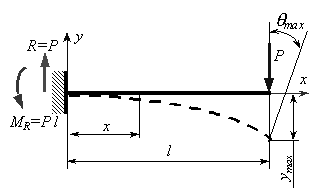
Для балки нагруженной распределенной нагрузкой найти аналитические выражения для прогибов и углов поворота.

 

Решение.

Изгибающий момент в произвольном поперечном сечении

.

В произвольном сечении на расстоянии x от опоры A имеем

.

Из условия для прогиба на левой опоре

.

Из условия для прогиба на правой опоре

.

Подставив значения C₁ и C₂ в уравнение, получим

.

На рисунке построены эпюры прогибов и углов поворота, из которых видно, что максимальный прогиб будет в середине балки

.

Максимальные углы поворота будут в опорных сечениях:

.

 

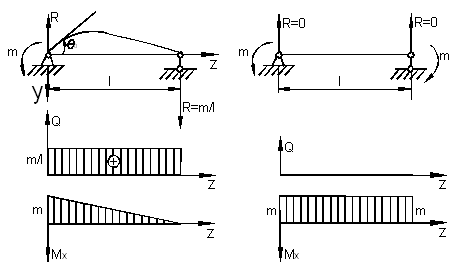
Пример 4.

Однопролетная шарнирно опертая балка находится под действием равномерно распределенной нагрузки (см. рис.).

Вывести дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

а) б)

Решение.

Опорные реакции в этой задаче Перерезывающая сила и изгибающий момент, согласно методу сечений, равны:

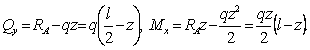(1)

Строим для наглядности эпюры (рис. а).

Подставляя найденное выражение для в дифференциальные урав­нения изогнутой оси балки, получим:

(2)

Интегрируя (2) дважды, находим:

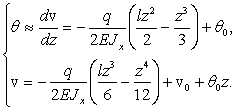(3)

На краях балки при имеем . Поэтому из (3) следует:

(4)

Подставляя полученные значения в (3), находим:

(5)

Максимальный прогиб имеет место в середине пролета при и равен:

(6)

Прогиб положителен, т.е. направлен вниз по оси у. Угол поворота . Геометрический смысл первой производной состоит в том, что она равна тангенсу угла наклона касательной в точке изогнутой оси с координатой z. На рис. б показано, в каких четвертях тангенс положителен и отрицателен, а также изображены фраг­менты касательных к изогнутой оси, отвечающие положительным и отрицательным углам поворота сечений

Перевернутая эпюра на рис. а построена на растянутых волокнах балки. Она напоминает изогнутую ось балки.

 

Пример 5.

1) Консольная балка изгибается силой Р на конце (см. рис. а).

2) Консольная балка изгибается распределенной нагрузкой (рис. б).

3) Консольная балка изгибается моментом на конце (рис. в).

Для всех трех балок найти дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

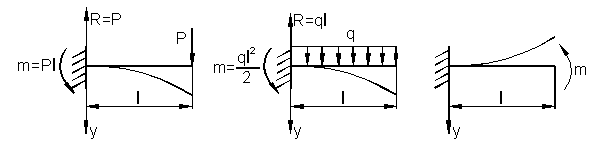
а) б) в)

 

Решение.

1) Из рис. а находим методом сечений:

(1)

Дифференциальное уравнение изгиба

(2)

Интегрируя, находим:

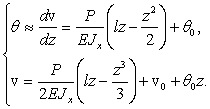(3)

При z = 0 имеем граничные условия:

(4)

Следовательно,

(5)

Максимальный прогиб и угол поворота имеют место на конце консоли при z = , т.е.

(6)

 

2) Из рис. б методом сечений находим:

(1)

Дифференциальное уравнение изгиба:

(2)

Интегрируя, получаем:

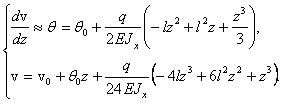(3)

В защемлении балки при z=0 имеем Максимальные угол поворота и прогиб имеют место на конце консоли при т.е.

(4)

3) В этом случае

Дифференциальное уравнение изгиба:

(1)

Интегрируя, получаем:

(2)

Так как при то получаем Следовательно,

(3)

 

Пример 6.

1) Изгиб однопролетной балки моментом в опоре (рис. а).

2) Чистый изгиб однопролетной балки моментами m (рис. б).

Для обеих балок найти дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

а) б)

 

Решение.

1) Перерезывающая сила и изгибающий момент в произвольном сечении z равны:

(1)

Дифференциальное уравнение изгиба:

(2)

откуда после интегрирования получаем:

(3)

Из граничных условий v = 0 при z = 0 и z = получаем:

(4)

Следовательно, 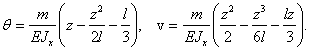(5)

Угол поворота на правой опоре:

(6)

2) В этом случае Дифференциальное уравнение изгиба:

(1)

откуда после интегрирования:

(2)

Из граничных условий при находим

Следовательно,

(3)

Максимальный прогиб в середине пролета:

(4)

 

Пример 7.

Определить вертикальное перемещение среднего и угол поворота торцевого сечения консольной балки.