
- •1 Основні поняття і визначення тпр
- •2 Матриця рішень
- •3 Поняття оцінювальної функції
- •4 Поле корисності рішень
- •5 Функція переваги
- •6 Особливі випадки матриці рішень
- •Критерій Баєса-Лапласа (bl)
- •10 Приклад застосування класичних критеріїв
- •15 Комбінований bl(mm)- критерій
- •17 Приклад застосування bl(mm)
- •18 Bl(s) - критерій
- •20 Дерево подій
- •21 Дерево рішень
- •23 Декомпозиція багатоетапного дерева рішень
- •25 Структуризація генеральної мети. Дерево цілей.
- •26 Оптимальність за Парето.
- •27 Необхідні та достатні умови оптимальності за Парето.
- •29 Оптимальність за Слейтером
- •30 Методи розв’язання багатокритерійних задач
- •31 Методи глобального критерію
- •32 Лінійне згортання критеріїв. Приклад.
- •33 Лінійне згортання нормованих критеріїв. Приклад.
- •34 Максимінне згортання критеріїв. Приклад.
- •36 Метод ідеальної точки. Приклад.
- •37 Методи переведення критеріїв у обмеження та послідовні поступки
- •38 Метод переведення критеріїв у обмеження
- •39 Метод лексикографічної оптимізації. Приклад.
- •41 Діалогові методи: метод оптимізації діленням відрізка навпіл, градієнтний метод
- •Метод наискорейшего спуска (метод градиента)
- •42 Методи з використанням бінарних відношень
- •43 Методи electre (I, II, III). Загальна характеристика.
- •44 Метод electre I.
- •Метод electre III
- •46 Багатоцільові рішення
15 Комбінований bl(mm)- критерій
Зафіксуємо за допомогою ММ-критерію значення
![]()
де i0,j0 – оптимізуючи індекси для всіх альтернативних варіантів рішень і зовнішніх станів.
Виберемо
рівень допустимого ризику
![]() та визначимо підмножину згоди, що є
підмножиною множини індексів
та визначимо підмножину згоди, що є
підмножиною множини індексів
![]() :
:
![]() .
.
Величина
![]() для всіх
для всіх
![]() характеризує найбільш можливі втрати
в порівнянні з
характеризує найбільш можливі втрати
в порівнянні з
![]() (за ММ-критерієм).
(за ММ-критерієм).
З іншого боку в результаті цього відкриваються і можливості для виграшу в порівнянні з тим, що забезпечується ММ-критерієм.
Тому розглядають також деяку виграшну множину
![]()
Тоді в
множині-перетині
![]() ми зберемо тільки такі варіанти рішень,
для яких, з одного боку, можуть мати
місце втрати в порівнянні з ММ-критерієм,
але зате в інших станах має місце, в
крайньому разі, такий же приріст виграшу
(а то й більший).
ми зберемо тільки такі варіанти рішень,
для яких, з одного боку, можуть мати
місце втрати в порівнянні з ММ-критерієм,
але зате в інших станах має місце, в
крайньому разі, такий же приріст виграшу
(а то й більший).
Тепер оптимальними в плані BL(MM) критерію будуть рішення із множини:

Правило вибору для BL(MM) критерію:
Матриця рішень доповнюється ще 3-ма стовпчиками:
в першому записуються математичні
сподівання кожного з рядків
![]() ;
;
в другому – різниці між опорним значенням
![]() і найменшим значенням
і найменшим значенням
![]() відповідного рядка;
відповідного рядка;
в третьому – різниці між найбільшим
значенням
![]() кожного рядка і найбільшим значенням
кожного рядка і найбільшим значенням
![]() того рядка, в якому знаходиться значення
.
Вибираються ті варіанти рішень, рядки
яких дають найбільше математичне
сподівання при умові, що значення другого
стовпчика має бути
того рядка, в якому знаходиться значення
.
Вибираються ті варіанти рішень, рядки
яких дають найбільше математичне
сподівання при умові, що значення другого
стовпчика має бути
![]() заданому рівню ризику
заданому рівню ризику
![]() ,
а значення третього стовпчика має бути
більше значення другого стовпчика.
,
а значення третього стовпчика має бути
більше значення другого стовпчика.
BL(MM) критерій добре пристосовується для побудови практичних рішень в першу чергу в області техніки і вважається досить надійним.
17 Приклад застосування bl(mm)
Застосування цього критерію зумовлено наступними ознаками ситуації, в якій приймається рішення: 1) ймовірності появи станів Fj невідомі, проте є деяка апріорна інформація на користь якогось певного розподілу; 2) необхідно рахуватися з появою різних станів як окремо, так і в комплексі; 3) допускається обмежений ризик; 4) прийняте рішення реалізується один раз або багаторазово. BL (MM)-критерій добре пристосований для побудови практичних рішень насамперед у галузі техніки і може вважатися досить надійним. Однак задані межі ризику і, відповідно, оцінок ризику не враховує ні число застосування рішення, ні іншу подібну інформацію. Вплив суб'єктивного фактора хоч і ослаблений, але не виключено повністю.
18 Bl(s) - критерій
Цей критерій є комбінацією критеріїв Баєса-Лапласа та Севіджа.
За опорну величину приймають
![]() ,
,
де
![]() .
.
Визначають допустиме значення ризику
Потім визначають підмножини I1 та I2:
![]()
![]()
де – допустима межа ризику:
Для
![]() маємо:
маємо:

20 Дерево подій


Топологічна схема (граф) може дати гарне загальне уявлення про стан деякої системи, альтернативні шляхи протікання і результати будь-якого процесу.
Розглянемо такий граф для прикладу 3-х паралельно працюючих агрегатів А1, А2, А3.
Позначення: А ‘і – відмова і-го агрегату; Аі – працездатний стан.
Ймовірність відмови в проміжок часу, що розглядається, однакова для кожного з 3-х агрегатів.
qi = 10-3, i = 1, 2, 3.
Дерево подій для випадку виходу із ладу 3-х паралельно працюючих агрегатів.
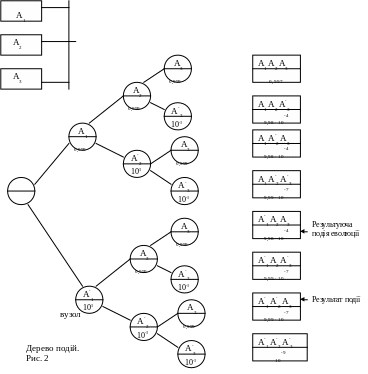
Початком схеми є кружок, що відповідає в загальному вигляді стану, що розглядається. З цього вузла гілки йдуть до вузлів, що відповідають стану першого агрегату (згідно з заданими ймовірностями) і т. д., поки на виході будуть отримані всі можливі комбінації.
В результаті отримаємо дерево подій, в якому кожний шлях від вихідного (початкового) вузла до кінцевого вузла описує одну з можливих еволюцій системи.
