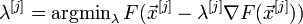- •1 Основні поняття і визначення тпр
- •2 Матриця рішень
- •3 Поняття оцінювальної функції
- •4 Поле корисності рішень
- •5 Функція переваги
- •6 Особливі випадки матриці рішень
- •Критерій Баєса-Лапласа (bl)
- •10 Приклад застосування класичних критеріїв
- •15 Комбінований bl(mm)- критерій
- •17 Приклад застосування bl(mm)
- •18 Bl(s) - критерій
- •20 Дерево подій
- •21 Дерево рішень
- •23 Декомпозиція багатоетапного дерева рішень
- •25 Структуризація генеральної мети. Дерево цілей.
- •26 Оптимальність за Парето.
- •27 Необхідні та достатні умови оптимальності за Парето.
- •29 Оптимальність за Слейтером
- •30 Методи розв’язання багатокритерійних задач
- •31 Методи глобального критерію
- •32 Лінійне згортання критеріїв. Приклад.
- •33 Лінійне згортання нормованих критеріїв. Приклад.
- •34 Максимінне згортання критеріїв. Приклад.
- •36 Метод ідеальної точки. Приклад.
- •37 Методи переведення критеріїв у обмеження та послідовні поступки
- •38 Метод переведення критеріїв у обмеження
- •39 Метод лексикографічної оптимізації. Приклад.
- •41 Діалогові методи: метод оптимізації діленням відрізка навпіл, градієнтний метод
- •Метод наискорейшего спуска (метод градиента)
- •42 Методи з використанням бінарних відношень
- •43 Методи electre (I, II, III). Загальна характеристика.
- •44 Метод electre I.
- •Метод electre III
- •46 Багатоцільові рішення
39 Метод лексикографічної оптимізації. Приклад.
У
методі лексикографічної оптимізації
передбачається, що критерії, що становлять
векторний критерій К, можуть бути
впорядковані на основі відношення
абсолютної переваги. Нехай критерії
пронумеровані так, що найбільш важливого
з них відповідає номер 1. Тоді на першому
кроці вибирається підмножина альтернатив
![]() які
мають найкращі оцінки за першим критерієм.
Якщо виявиться, що то єдина альтернатива,
яка входить до А1 і визнається
найкращою.
Якщо
які
мають найкращі оцінки за першим критерієм.
Якщо виявиться, що то єдина альтернатива,
яка входить до А1 і визнається
найкращою.
Якщо
![]() то на другому кроці вибирається підмножина
альтернатив
то на другому кроці вибирається підмножина
альтернатив
![]() які
мають найкращі оцінки за другим критерієм,
і так далі, до тих пір, поки не буде
виявлена краща альтернатива.
які
мають найкращі оцінки за другим критерієм,
і так далі, до тих пір, поки не буде
виявлена краща альтернатива.
Метод лексикографічної оптимізації застосовується тоді, коли критерії чітко ранжовані за пріоритетом, причому кожен наступний критерій абсолютно менш важливий, ніж попередній, тобто ус- тупка по першому критерію не компенсується ніяким приростом по іншому [27]. даний метод зводить рішення багатокритеріальної задачі до ряду однокрітеріальним, коли спочатку оптимізується перший критерій, далі - другий за умови, що значення першого залишається максимальним, і т.д.
пример выбора варианта лексикографическим методом.
Пусть в результате экспертной оценки получили следующие данные, характеризующие степень соответствия СЗИ Система защиты информации заданным требованиям:

10. Требования упорядочены по важности следующим образом
С1 >C2 >C3 >C4
20. Зададимся величиной допустимой уступки
D Сі = 0,1 для всех
![]() .
.
30. Формируем множество p 1 по первому требованию. При максимальном значении С1 = 0,9 и D С1 = 0,1 в это множество входят варианты p 1 = {a1, a2, a3}.
40. Из элементов множества p 1
формируем множество p 2 по второму
требованию. При
![]() множество
p 2 = {a1, a2}.
множество
p 2 = {a1, a2}.
50. Из элементов множества p = p 1
х p 2 формируем множество p 3
по третьему требованию. При
![]() это
множество содержит один элемент
p 3
= a2.
это
множество содержит один элемент
p 3
= a2.
Таким образом, наилучшим вариантом является второй вариант СЗИ.
40 Метод послідовних поступок. Приклад =37
41 Діалогові методи: метод оптимізації діленням відрізка навпіл, градієнтний метод
Метод
половинного деления (метод
бисекции)
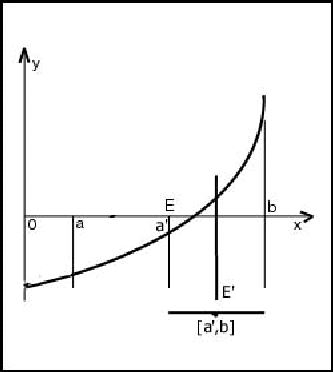 рис.2
Метод
половинного деления (известный еще и
как «метод деления отрезка пополам»)
также является рекурсивным, т.е.
предусматривает повторение с учетом
полученных результатов.
Суть
метода половинного деления заключается
в следующем:
дана функция F(x);
определена допустимая погрешность
Q; определен
некоторый интервал [ a , b
], точно содержащий решение
уравнения.
Вычисляем значение
координаты Е, беря середину отрезка [a
, b], т.е. Е= (a
+ b ) / 2 (7)
Вычисляем
значения F(a),
F(b), F(E),
и осуществляем следующую проверку: Если
F(E)>Q,
то корень с указанной точностью найден.
Если F(E)<Q,
т.е. необходимая точность еще не
достигнута, то формируем два интервала:
[a , E] и [E
, b] проверяем знаки F(a),
F(b), F(E).
На концах одного из этих интервалов
знаки функции будут одинаковы, а на
друго различны (иначе Е - искомый корень).
И именно то интервал, на концах которого
знаки различны, мы берем за основу при
следующей итерации, т.е. приравниваем
к Е либо a, либо b.
рис.2
Метод
половинного деления (известный еще и
как «метод деления отрезка пополам»)
также является рекурсивным, т.е.
предусматривает повторение с учетом
полученных результатов.
Суть
метода половинного деления заключается
в следующем:
дана функция F(x);
определена допустимая погрешность
Q; определен
некоторый интервал [ a , b
], точно содержащий решение
уравнения.
Вычисляем значение
координаты Е, беря середину отрезка [a
, b], т.е. Е= (a
+ b ) / 2 (7)
Вычисляем
значения F(a),
F(b), F(E),
и осуществляем следующую проверку: Если
F(E)>Q,
то корень с указанной точностью найден.
Если F(E)<Q,
т.е. необходимая точность еще не
достигнута, то формируем два интервала:
[a , E] и [E
, b] проверяем знаки F(a),
F(b), F(E).
На концах одного из этих интервалов
знаки функции будут одинаковы, а на
друго различны (иначе Е - искомый корень).
И именно то интервал, на концах которого
знаки различны, мы берем за основу при
следующей итерации, т.е. приравниваем
к Е либо a, либо b.
Классический градиентный метод оптимизации состоит в итерационном уточнении аргумента согласно формуле:

Метод минимизации функции многих переменных (целевой функции). Он состоит в том, что последующее приближение функции получается из предыдущего путем смещения в направлении, противоположном ее градиенту.
Основная идея методов заключается в
том, чтобы идти в направлении наискорейшего
спуска, а это направление задаётся
антиградиентом
![]() :
:
![]()
где
![]() выбирается
выбирается
постоянной, в этом случае метод может расходиться;
дробным шагом, то есть длина шага в процессе спуска делится на некое число;
наискорейшим спуском: