3. Дифференциальные уравнения с разделяющимися переменными

Определение 1. Уравнение вида называется уравнением с разделяющимися переменными.

Если для некоторого выполняется условие , то функция является решением уравнения.

Если , то получаем равносильное уравнение . Это уравнение, в случае непрерывности функций и при рассматриваемых значениях x и y , равносильно уравнению .

Действительно, обозначим через некоторую первообразную функции , через - некоторую первообразную функции . Тогда , . Следовательно,

.

Но дифференциалы двух функций (переменной x) равны тогда и только тогда, когда сами функции различаются на постоянное слагаемое:

.

4. Однородные и линейные дифференциальные уравнения 1-го порядка и их решения

Определение 1. Однородным уравнением первого порядка называется дифференциальное уравнение первого порядка, которое может быть представлено в виде

,

где f – некоторая функция одной переменной.

Метод решения однородного дифференциального уравнения: вводим новую переменную . Следовательно, . Получаем уравнение с разделяющимися переменными относительно переменной z:

.

Определение 2. Линейным уравнением первого порядка называется дифференциальное уравнение первого порядка, которое линейно относительно функции y и ее производной , т.е. уравнение вида

Определение 2. Если , то уравнение вида называется однородным линейным уравнением первого порядка.

Однородное линейное уравнение первого порядка является уравнением с разделяющимися переменными: . Функция y=0 является решением этого уравнения.

Если же , то получаем , тогда . Если - некоторая первообразная функции , то

.

Итак, общее решение однородного линейного уравнения имеет вид

.

В общем случае, т.е. если , уравнение называется неоднородным линейным уравнением первого порядка.

Имеется несколько способов решения неоднородных линейных уравнений. Рассмотрим метод вариации постоянной. Общее решение ищем в виде

,

где - неизвестная функция.

Подставляя в уравнение y и , имеем

,

следовательно,

,

.

Подставляя найденное значение , получаем общее решение

,

которое является суммой общего решения соответствующего однородного линейного уравнения и частного решения линейного неоднородного уравнения.

Лекция 14 Тема 14. Числовые ряды

ПЛАН

1. Определение числового ряда. Сходимость числового ряда.

2. Признаки сравнения и признак Даламбера сходимости знакоположительных рядов.

3. Интегральный признак сходимости числовых рядов.

4. Теорема Лейбница. Абсолютная и условная сходимости рядов.

1. Определение числового ряда. Сходимость числового ряда

Определение 1. Если члены числовой последовательности (a_n) соединить знаком «+», то полученное формальное выражение а₁+а₂+а₃+…+a_n+… называется числовым рядом.

Числовой ряд будем также записывать символом или просто . Число а_n называется n-м или общим членом ряда.

Договоримся, что если некоторые члены ряда имеют отрицательные знаки, то можно писать, например, вместо выражения .

Определение 2. Сумма первых п членов числового ряда называется n-ой частичной суммой ряда и обозначается S_n=а₁+а₂+а₃+…+a_n .

По определению имеем S₁=a₁, S₂=a₁+a₂, S₃=a₁+a₂+a₃ и т.д. . Возникает новая числовая последовательность (S_n).

Определение 3. Если последовательность (S_n) частичных сумм числового ряда сходится к некоторому числу SR, то этот числовой ряд называется сходящимся.

Определение 4. Если числовой ряд сходится, то число называется суммой числового ряда и пишут S= или S=a₁+a₂+a₃+…+а_n+... .

Итак, символом будем обозначать и числовой ряд, и его сумму (если ряд сходится).

Подчеркнем, что S не есть "сумма всех членов ряда", а является пределом последовательности его частичных сумм, т.е. .

Определение 5. Числовой ряд называется расходящимся, если последовательность (S_n) его частичных сумм расходится.

Определение 6. Суммой двух числовых рядов и называется числовой ряд .

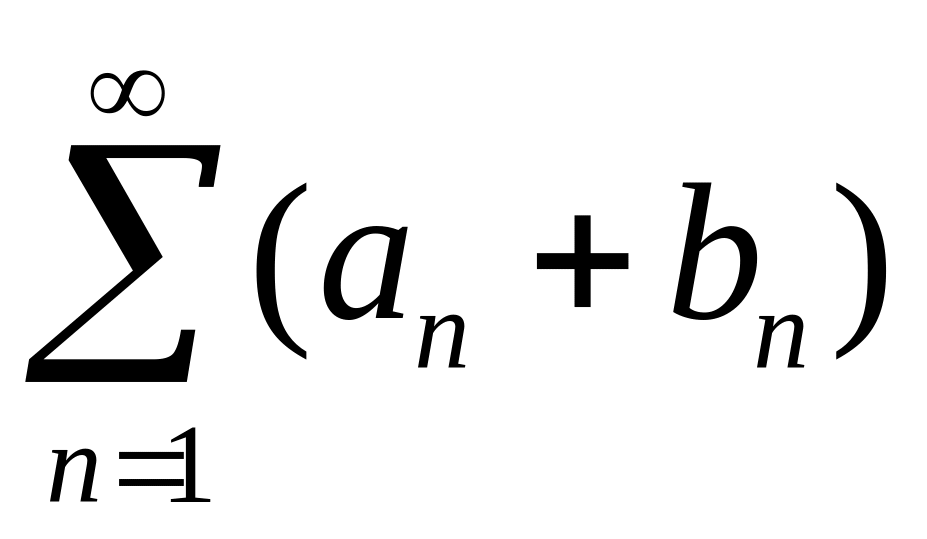Теорема 1. Если числовые ряды и сходятся и имеют суммы A и B , то числовой ряд также сходится и имеет сумму A+B .

Определение 7. Произведением числового ряда на число kR называется числовой ряд .

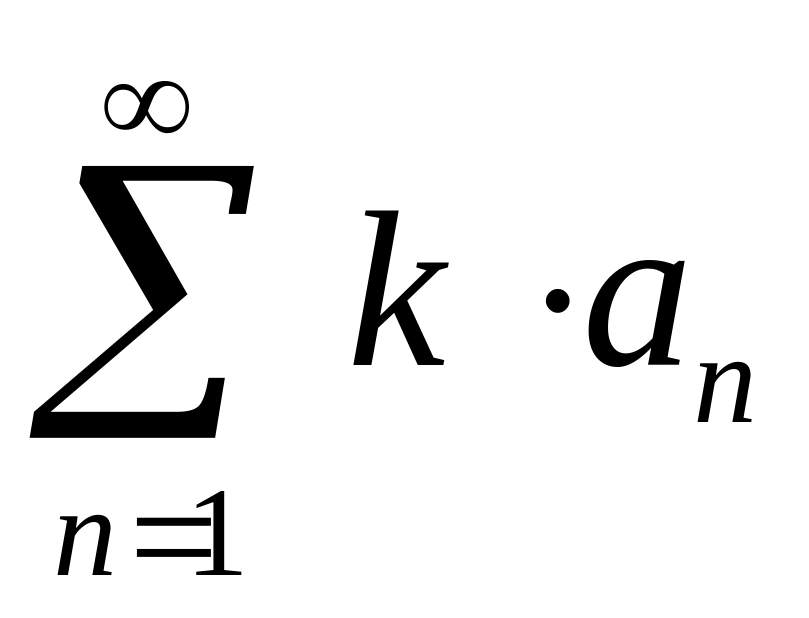Теорема 2. Если числовой ряд сходится и имеет сумму A , то числовой ряд также сходится для любого kR и имеет сумму kA .

Для исследования числовых рядов на сходимость имеется ряд признаков. Далее рассмотрим некоторые из них.

Теорема 3. (необходимое условие сходимости числового ряда). Если числовой ряд сходится, то .

Доказательство. Ряд сходится, т.е. существует предел . Заметим, что .

Рассмотрим . Тогда . Отсюда, .

Следствие 1. Если не выполнено условие , то ряд расходится.

Замечание 1. Условие не является достаточным для сходимости числового ряда . Например, гармонический ряд расходится, хотя и имеет место .

Определение 8. Числовой ряд a_n+1+a_n+2+…=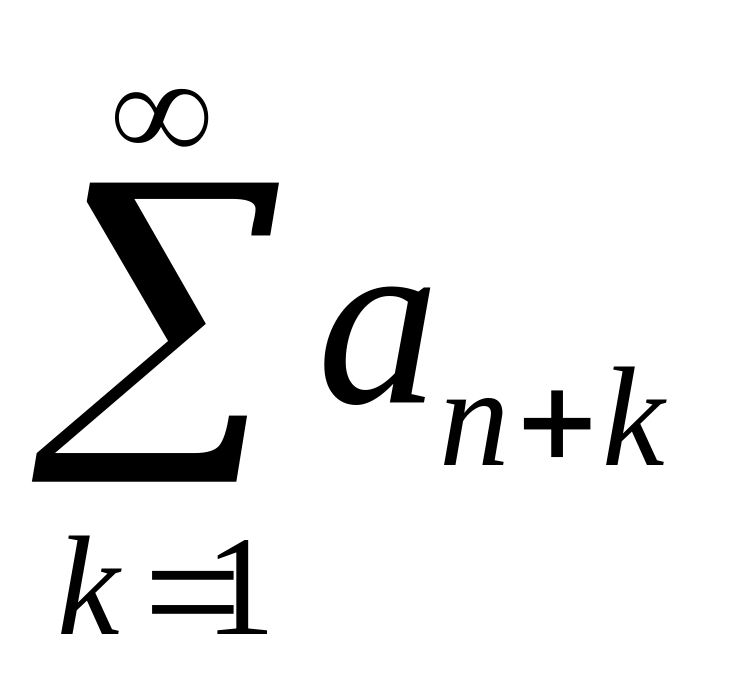 , полученный из данного ряда отбрасыванием первых п членов, называется n-м остатком данного ряда и обозначается R_n .

Теорема 4. Если числовой ряд сходится, то сходится и любой его остаток. Обратно: если сходится хотя бы один остаток ряда, то сходится и сам ряд. При этом, для любого n выполняется равенство S=S_n+R_n .

Следствие 2. Сходимость или расходимость числового ряда не изменится, если удалить или добавить несколько первых членов.

Следствие 3.   .

нов ряда , что ряд сходится и его сумма равна C .