Так, наприклад, якщо , то

.

Звідси

(використані властивості (3) і (4)).

5. «Теорема про середнє». Якщо функція неперервна на відрізку , то існує точка така, що

.

□ По формулі Ньютона-Лейбніца маємо

,

де . Застосовуючи до різниці теорему Лагранжа (теорему про скінчевий приріст функції), отримаємо

.■

Властивість (5) («Теорема про середнє») при має простий геометричний зміст: значення визначеного інтеграла дорівнює, при деякому , площі прямокутника з висотою і основою (див. рис. 170).

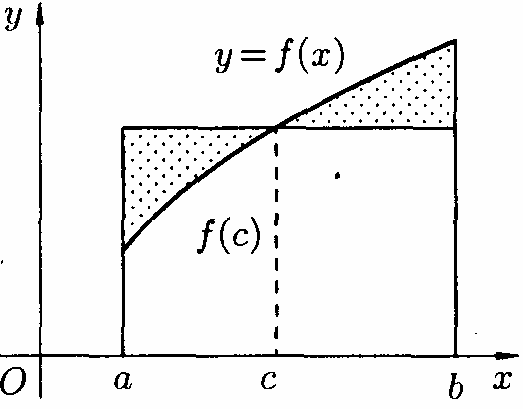
(рис.170)

Число називається середнім значенням функції на відрізку .

6. Якщо функція зберігає знак на відрізку , де 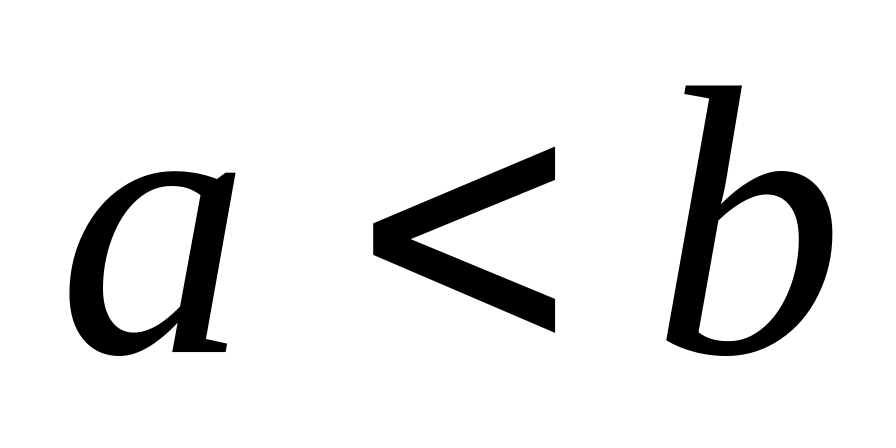, то інтеграл має той же знак, що і функція. Так, якщо на відрізку , то .

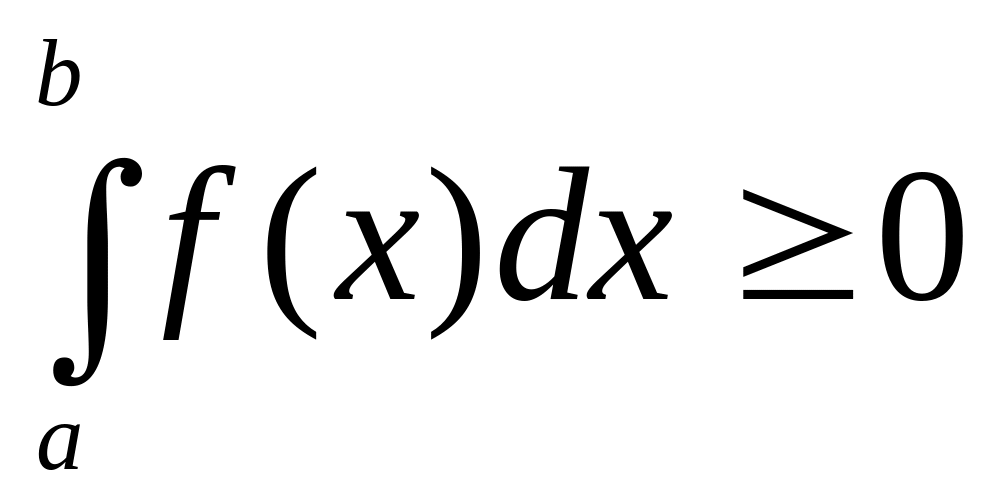За «теоремою про середнє» (властивість (5))

, де . А оскільки для всіх , то і

.

Тому , тобто .

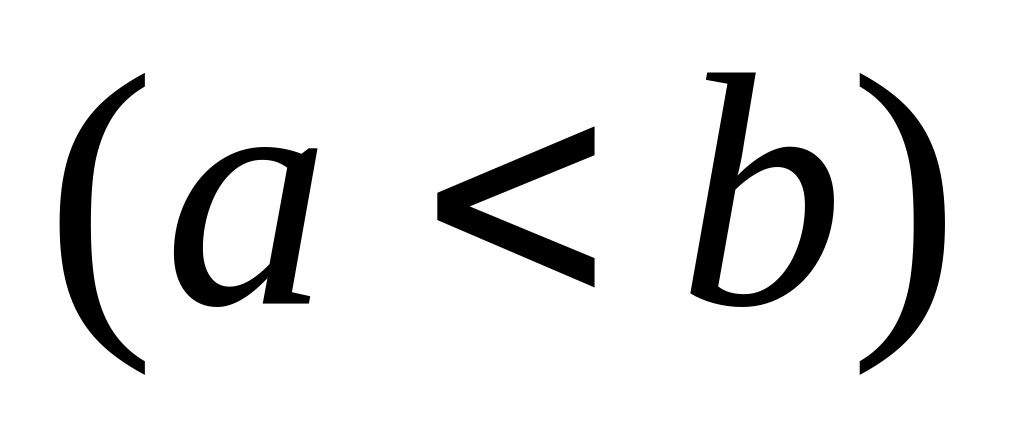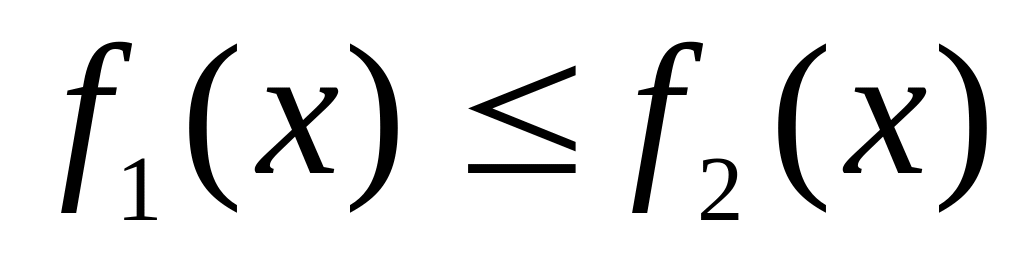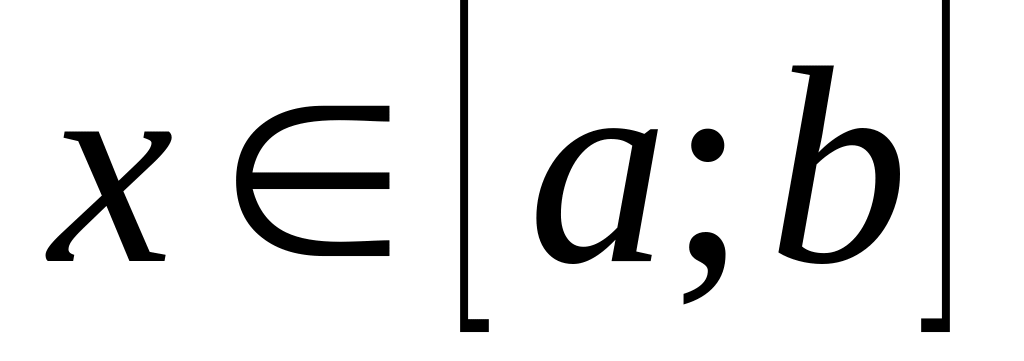7. Нерівність між неперервними функціями на відрізку , можна інтегрувати. Так, якщо при , то .

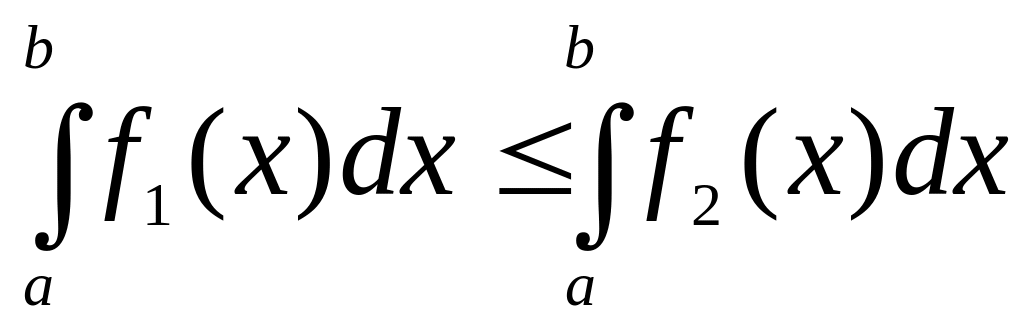Оскільки , то при , згідно властивості (6), маємо

.

Або, згідно властивості (2)

, тобто .

Відзначимо, що диференціювати нерівності не можна.

8. Оцінка інтеграла. Якщо т і М — відповідно найменше і найбільше значення функції на відрізку , , то

.

Застосовуючи до крайніх інтегралів властивість (5), отримаємо

.

Якщо , та властивість (8) ілюструється геометрично: площа криволінійної трапеції вкладена між площами прямокутників, основою яких є , а висоти рівні і (див. рис.171).

(рис.171)

9. Модуль визначеного інтеграла не перевершує інтеграла від модуля підінтегральної функції:

.

Застосовуючи властивість (7) до очевидних нерівностей , отримаємо .

Звідси слідує, що .

10. Похідна визначеного інтеграла по змінній

верхній межі дорівнює підінтегральній функції, в якій змінна інтегрування замінена цією межею, тобто

.

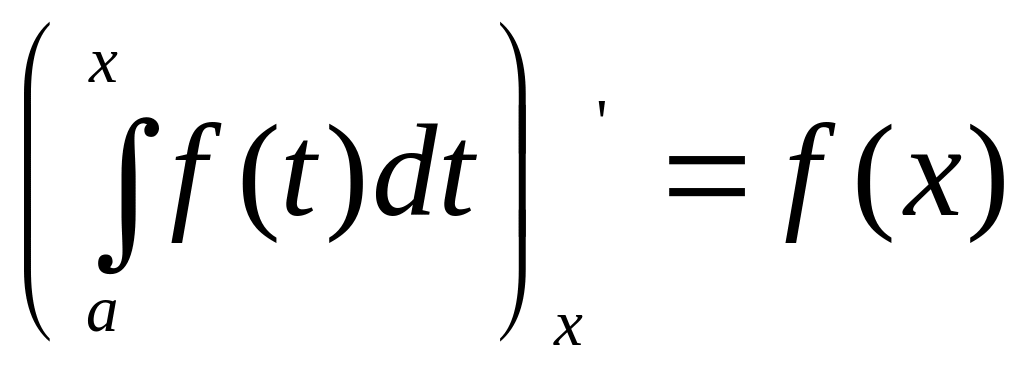По формулі Ньютона-Лейбніца маємо: .

Отже,

.

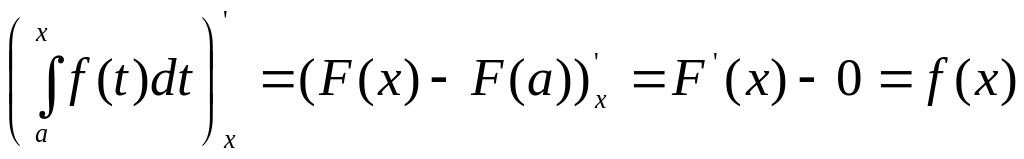Це означає, що визначений інтеграл із змінною верхньою межею є одна з первісних підінтегральних функцій.

Формула Ньютона-Лейбніца

Нехай функція інтегрована на відрізку .Точки розриву 1 роду

Теорема 9.3.1 Якщо функція неперервна на відрізку і — яка-небудь її первісна, то має місце формула

. (9.3.1)

□ Розіб'ємо відрізок точками на частинних відрізків , так як це показано на рис.169.

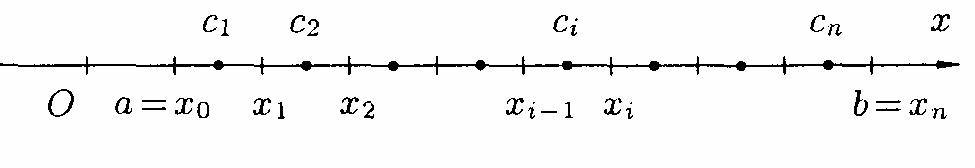
(рис.169)

Розглянемо тотожність

.

Перетворимо кожну різницю в дужках по формулі Лагранжа

.

Отримаємо

.

тобто

,

де є деяка точка інтервалу . Так як функція неперервна на . Тому існує границя інтегральної суми, що дорівнює визначеному інтегралу від на .

Переходячи в рівності (9.3.2) до границі при , отримаємо

,

тобто

.■

Рівність (9.3.1) називається формулою Ньютона-Лейбніца.

Якщо ввести позначення , то формулу Ньютона-Лейбніца можна переписати так:

.

Формула Ньютона–Лейбница дає зручний спосіб обчислення визначеного інтеграла. Щоб обчислити визначений інтеграл від неперервної функції на відрізку , треба знайти її первісну функцію і узяти різницю значень цієї первісної на кінцях відрізка .