
- •61.Інтегрування правильних дробів, раціональних дробів, ірраціональостей.
- •63.Визначений інтеграл як границя інтегральної суми
- •64. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Формула Ньютона-Лейбніца
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •65. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •Використовуючи формулу (9.5.2), отримаємо
- •Невласні інтеграли.
- •9.6.1. Інтеграл з нескінченним проміжком інтегрування
- •66.Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •2. Рівняння Бернуллі
- •3. Рівняння Рікатті Рівняння вигляду
63.Визначений інтеграл як границя інтегральної суми

(рис.167)
Нехай
функція
![]() визначена на відрізку
визначена на відрізку
![]() .
Виконаємо наступні дії.
.
Виконаємо наступні дії.
За допомогою точок
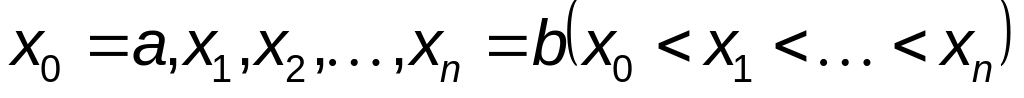 розіб'ємо відрізок
розіб'ємо відрізок
![]() на n
частинних
відрізків
на n
частинних
відрізків
![]() (дивися рис. 167).
(дивися рис. 167).
В кожному частинному відрізку
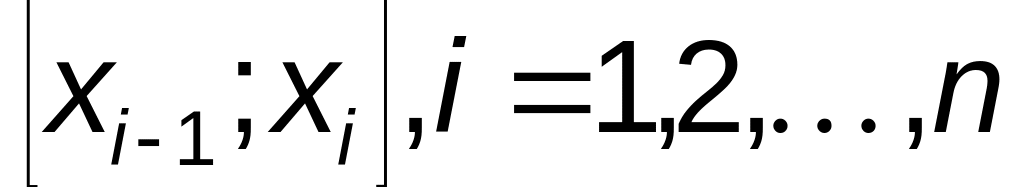 виберемо довільну точку
виберемо довільну точку
![]() і
обчислимо значення функції в ній, тобто
величину
і
обчислимо значення функції в ній, тобто
величину
![]() .
.
Помножимо знайдене значення функції
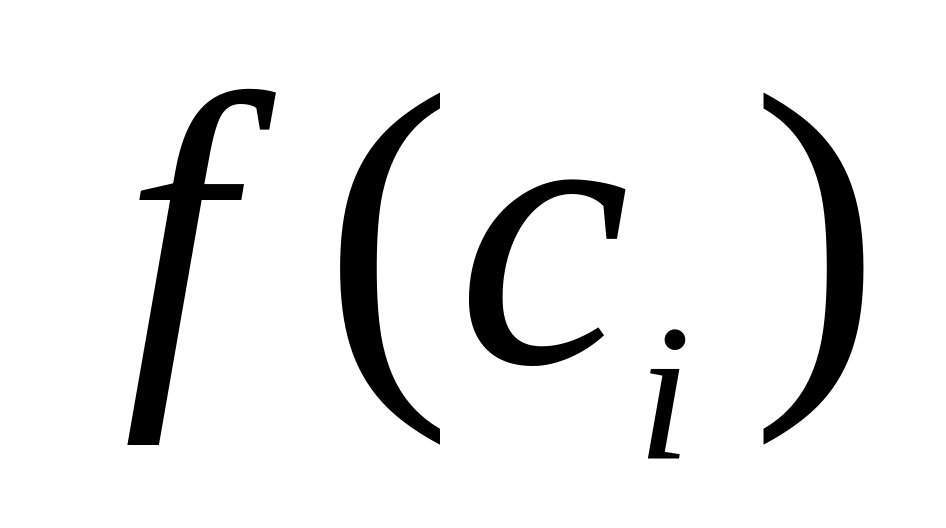 на довжину
на довжину
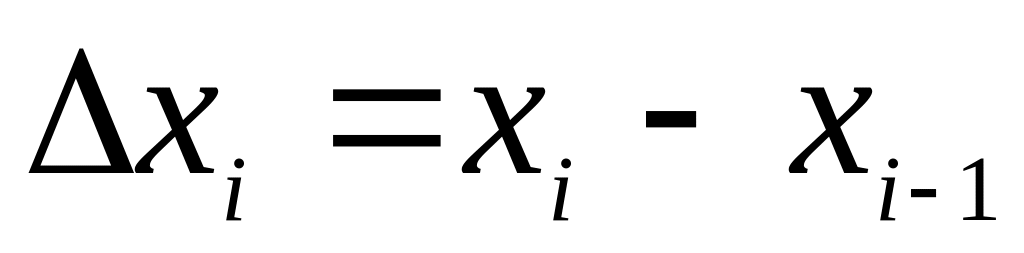
відповідного
частинного відрізка:
![]() .
.
Складемо суму
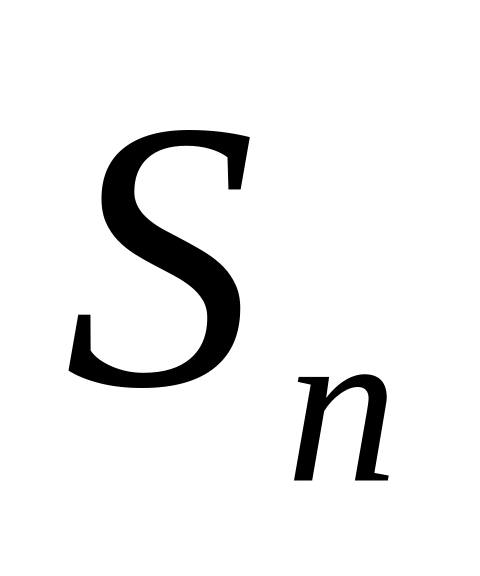 всіх таких добутків:
всіх таких добутків:
![]() .
(9.1.1)
.
(9.1.1)
Сума
вигляду (9.1.1) називається інтегральною
сумою
функції
![]() на відрізку
на відрізку
![]() .
.
Позначимо
через
![]() довжину найбільшого частинного відрізка:
довжину найбільшого частинного відрізка:
![]() .
.
Знайдемо границю інтегральної суми (1.1), коли
 так, щоб
так, щоб
 .
.
Якщо
при цьому інтегральна сума
має границю, яка не залежить ні від
способу розбиття відрізка
![]() на частинні відрізки, ні від вибору
точок в них, то вона називається визначеним
інтегралом
від
функції
на частинні відрізки, ні від вибору
точок в них, то вона називається визначеним
інтегралом
від
функції
![]() на відрізку
і позначається
на відрізку
і позначається
![]() .
(9.1.2)
.
(9.1.2)
Числа
![]() і
і
![]() називаються відповідно нижньою і
верхньою межами інтегрування,
називаються відповідно нижньою і
верхньою межами інтегрування,
![]() -
підінтегральною функцією,
-
підінтегральною функцією,
![]() -
підінтегральним виразом,
-
підінтегральним виразом,
![]() -
змінною інтегрування, відрізок
- областю (відрізком) інтегрування.
-
змінною інтегрування, відрізок
- областю (відрізком) інтегрування.
Функція
для якої на відрізку
існує визначений інтеграл
![]() ,
називається інтегрованою на цьому
відрізку.
,
називається інтегрованою на цьому
відрізку.
Сформулюємо тепер теорему існування визначеного інтеграла.
Теорема
Коші.
Якщо
функція
неперервна на відрізку
,
то визначений інтеграл
![]() існує.
існує.
Відзначимо, що неперервність функції є достатньою умовою її інтегрованості. Проте визначений інтеграл може існувати і для деяких розривних функцій, зокрема для всякої обмеженої на відрізку функції, що має на ній скінчене число точок розриву.
Вкажемо деякі властивості визначеного інтеграла, які безпосередньо випливають з його означення (9.1.2).
Визначений інтеграл не залежить від позначення змінної інтегрування:
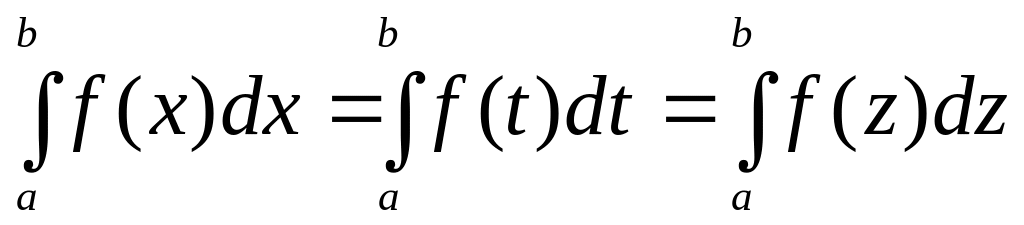 .
Це випливає з того, що інтегральна сума
(9.1.1), а отже, і границя (9.1.2) не залежать
від того, якою буквою позначається
аргумент даної функції.
.
Це випливає з того, що інтегральна сума
(9.1.1), а отже, і границя (9.1.2) не залежать
від того, якою буквою позначається
аргумент даної функції.Визначений інтеграл з однаковими межами інтегрування рівний нулю:
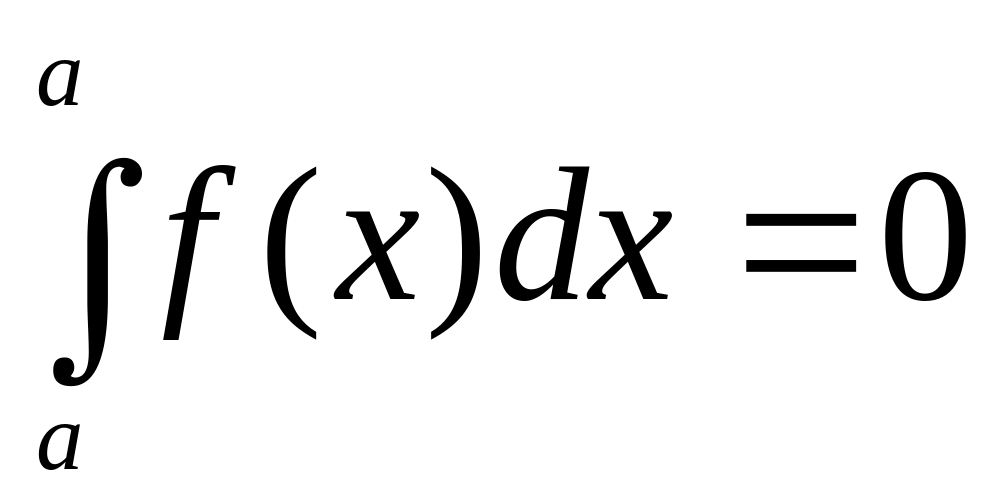 .
3.Для будь-якого дійсного числа
.
3.Для будь-якого дійсного числа
 :
:
 .
.
64. Основні властивості визначеного інтеграла
Розглянемо
основні властивості визначеного
інтеграла, вважаючи підінтегральну
функцію інтегрованою на відрізку
![]() .
При виведенні властивостей
використовуватимемо означення інтеграла
і формулу Ньютона-Лейбніца.
.
При виведенні властивостей
використовуватимемо означення інтеграла
і формулу Ньютона-Лейбніца.
Якщо
 — постійне число і функція
інтегрована на
— постійне число і функція
інтегрована на
то постійний множник можна виносити за знак визначеного інтеграла.
![]() (9.4.1)
(9.4.1)
Складемо
інтегральну суму для функції
![]() .
Маємо :
.
Маємо :
![]() .
.
Тоді
![]() .
Звідси випливає, що функція
.
Звідси випливає, що функція
![]() інтегрована на
і справедлива формула (9.4.1).
інтегрована на
і справедлива формула (9.4.1).
Якщо функції
 і
і
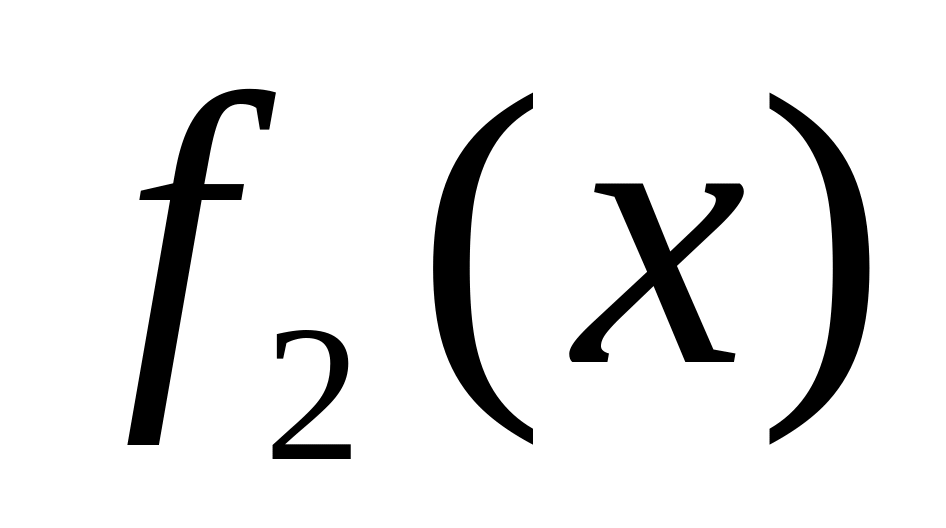 інтегровані на
,
тоді інтегрована на
їх сума і
інтегровані на
,
тоді інтегрована на
їх сума і
![]() (9.4.2)
(9.4.2)
тобто інтеграл від суми рівний сумі інтегралів.
![]()
![]() .
.
Властивість (2) розповсюджується на суму будь-якого скінченного числа доданків.
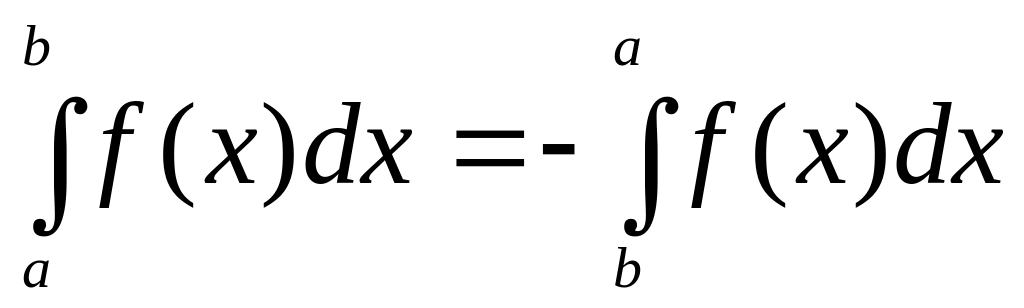 .
Цю властивість можна прийняти за
означенням. Ця властивість також
підтверджується формулою Ньютона-Лейбніца.
.
Цю властивість можна прийняти за
означенням. Ця властивість також
підтверджується формулою Ньютона-Лейбніца.
![]() .
.
Якщо функція
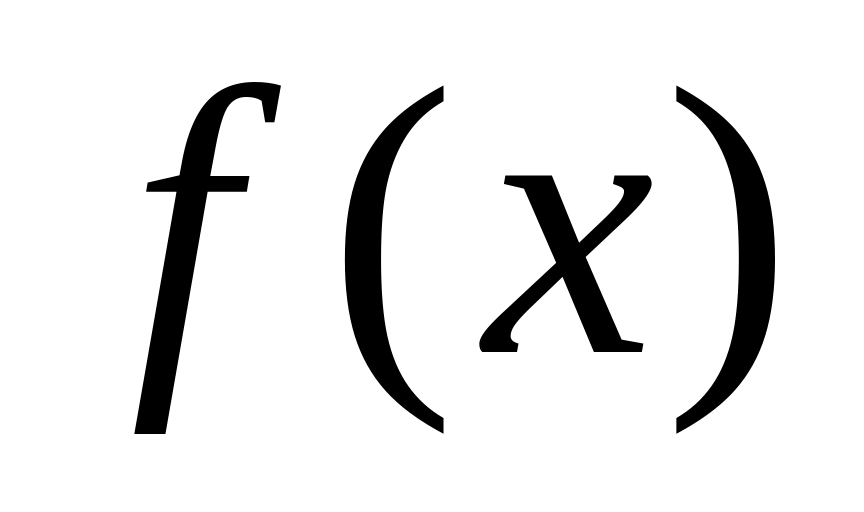 інтегрована на
інтегрована на
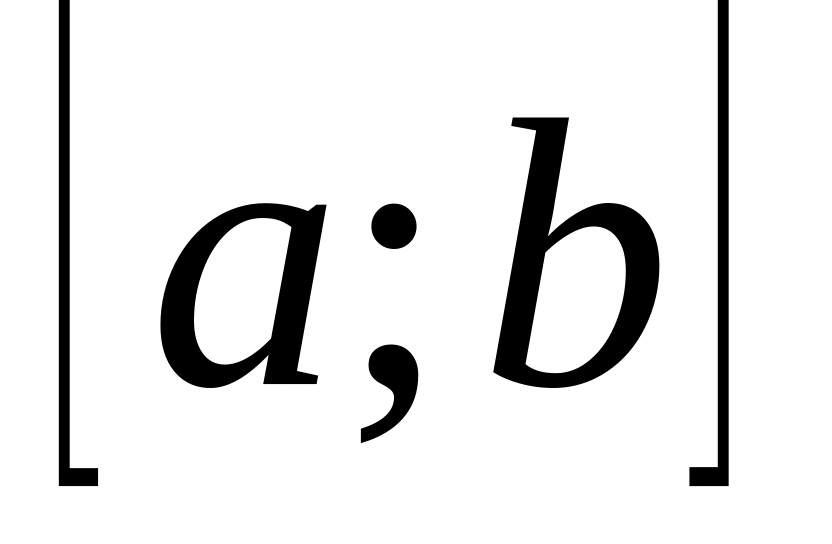 і
і
 ,
то
,
то
![]() (9.4.3)
(9.4.3)
тобто інтеграл по всьому відрізку дорівнює сумі інтегралів по частинах цього відрізка. Цю властивість називають аддитивністю визначеного інтеграла (або властивістю аддитивності).
При
розбитті відрізка
на частини включимо точку
в число точок поділу (це можна зробити
зважаючи на незалежність границі
інтегральної суми та способу розбиття
відрізка
на частини). Якщо
![]() ,
то інтегральну суму можна розбити на
дві суми:
,
то інтегральну суму можна розбити на
дві суми:
![]() .
.
Кожна
з написаних сум є інтегральною відповідно
для відрізків
,,![]() ,,
,,![]() .
Переходячи до границі в останній рівності
при
.
Переходячи до границі в останній рівності
при
![]() ,
отримаємо рівність (38.3).
,
отримаємо рівність (38.3).
Властивість
(4) справедлива при будь-якому розташуванні
точок
![]() (вважаємо, що функція
інтегрується на більшому з відрізків).
(вважаємо, що функція
інтегрується на більшому з відрізків).
