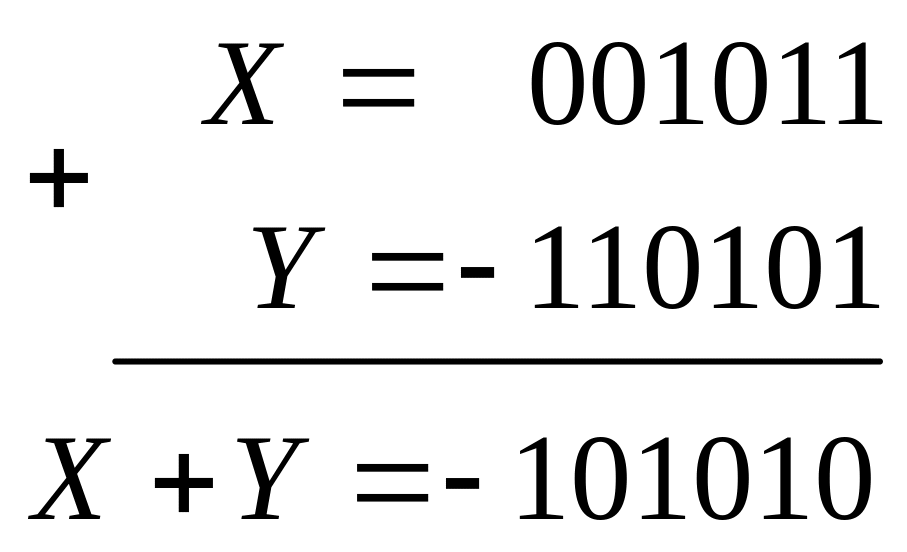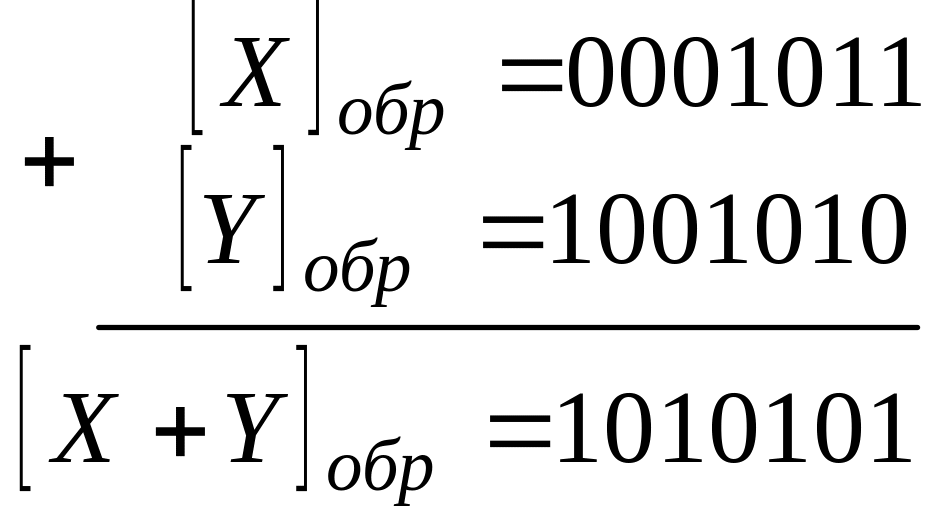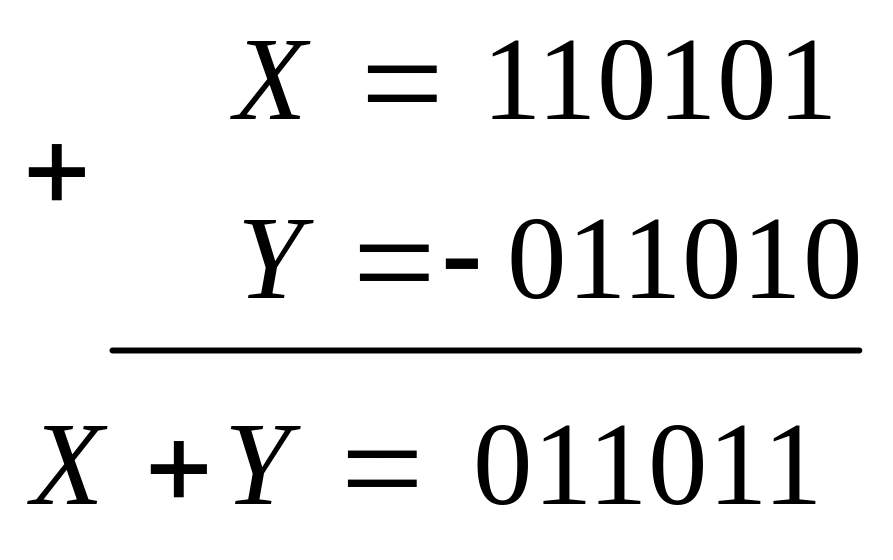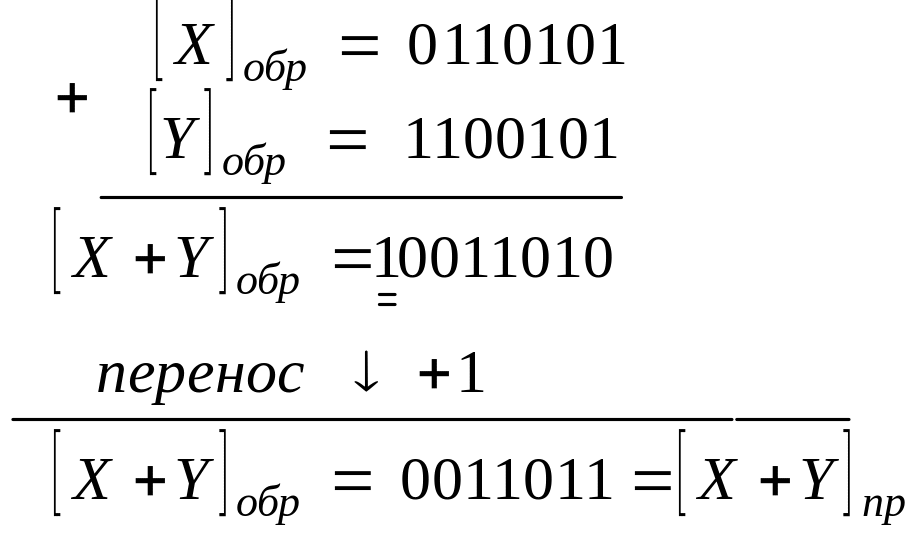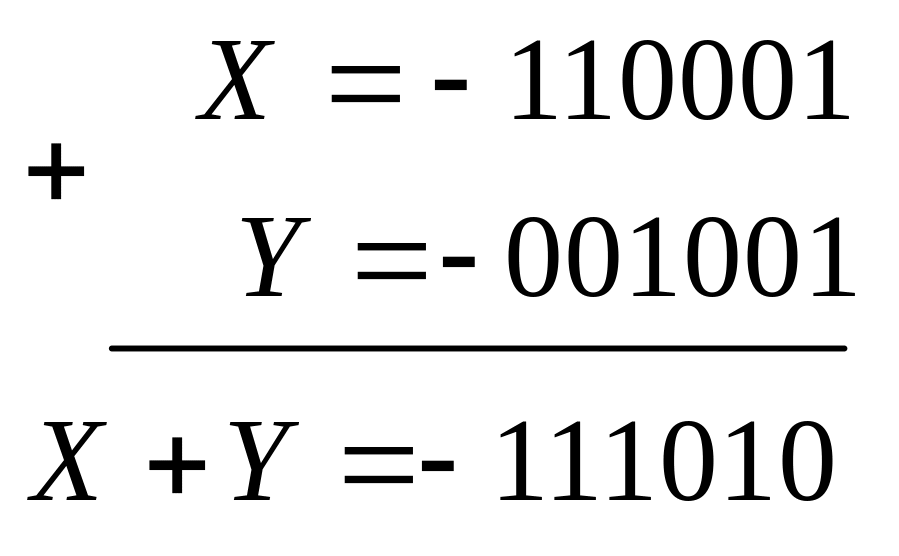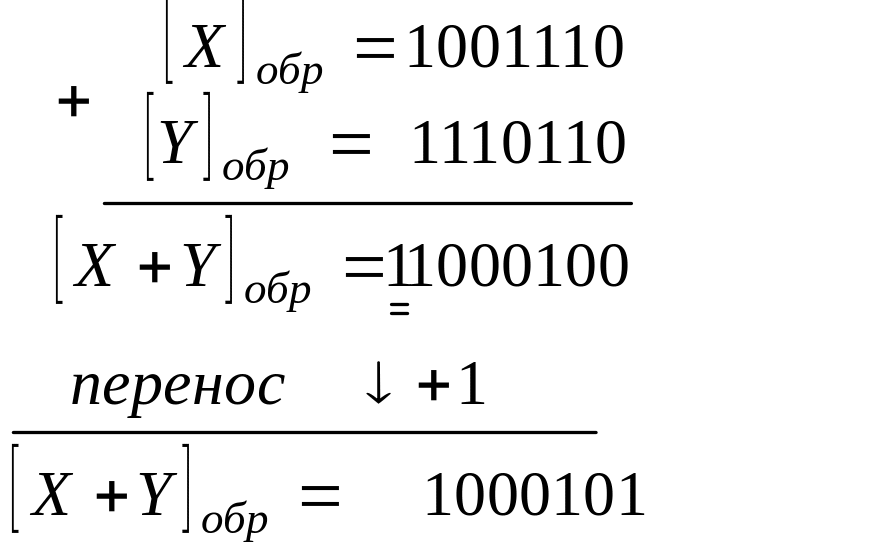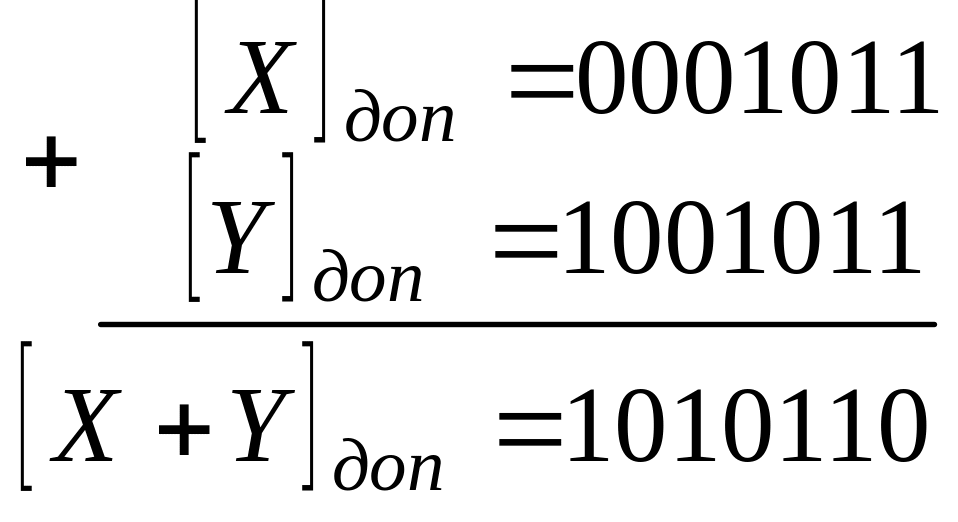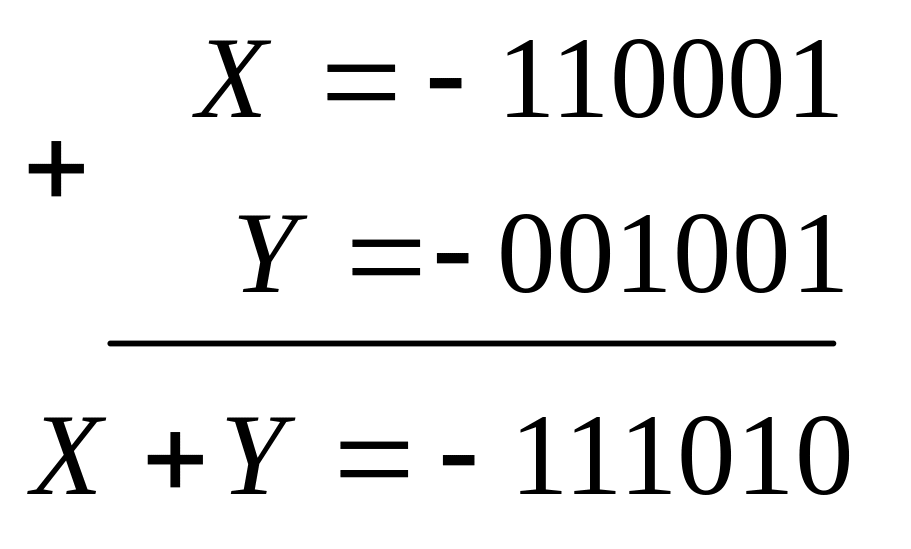Принцип сложения и вычитания двоичных чисел в эвм

В цифровой ЭВМ любая информация (числовая, символьная, команда, операции и т.д.) представлена в двоичном коде, т.е. в виде комбинаций 0 и 1. Для того, чтобы машина могла отли­чать один вид информации от другого, ее обычно размешают и хранят в разных регистрах. Так, например, коды команд обяза­тельно хранятся в регистре команд, данные - в регистре данных и т.д. Если команда будет записана в регистр данных, то она бу­дет прочитана машиной как число, а число, записанное в регистр команд, будет воспринято как команда. Кроме того, машина должна различать положительные числа и отрицательные, целые и дробные, что необходимо при выполнении арифметических и логических опера­ций.

В данной работе рассматриваются принципы выполнения в ЭВМ арифметических операций сложения и вычитания. Их схемотехничес­кая реализация зависит, во-первых, он формы представления двоич­ных чисел, во-вторых, от типа используемых кодов. В вычислитель­ной технике используются две формы представления двоичных чисел: с фиксированной запятой (точкой) - естественная форма, и с плаваю­щей запятой (точкой) - полулогарифмическая или нормальная форма. Рассмотрим первую форму, используемую в данной работе.

Для кодирования чисел в ЭВМ используется одно машинное сло­во, представляющее собой совокупность двоичных разрядов, называе­мое разрядной сеткой. В различных типах ЭВМ слова могут быть 2-байтовыми (16 разрядов), 4- байтовыми (32 разряда) и 8-байтовыми (64 разряда).

При любой форме представления двоичного числа (естественной или нормальной) под знак используется старший бит разрядной сет­ки числа. Если число положительное, то старший знаковый бит ра­вен 0, если число отрицательное, то знаковый бит равен 1. Поло­жение запятой (точки) строго фиксировано после определенного раз­ряда и делит число на целую и дробную часть. Запятая может быть зафиксирована программистом в любом месте разрядной сетки, одна­ко, чаще всего запятая фиксируется или перед первым (старшим) цифровым разрядом, или после младшего (крайнего правого) разря­да. В первом случае в разрядной сетке можно изобразить правильные дроби и машина оперирует с числами меньшими единицы. Во втором случае в разрядной сет­ке будут изображаться целые числа. Следует понимать, что запятая подразумевается программистом и машиной никак не фиксируется. Позиция запятой имеет значение только для програм­миста, который при составлении программы должен ввести в маши­ну масштабные коэффициенты и преобразовать обрабатываемые числа либо в правильные дроби, либо в целые числа. При получении окон­чательного результата все введенные коэффициенты масштабирова­ния должна быть учтены.

Знак числа

…..

Знак числа

…..

Казалось бы, такие сложности не оправданы, и представление чисел с фиксированной запятой не может иметь распространение в практике. Однако, существует целый класс задач, так называемые "деловые", где заранее известен порядок чисел и результата, на­пример, часто встречающиеся финансовые задачи, где подсчитываются деньги в копейках (или рублях) с точностью, например, до 0,01 коп, т.е. все числа не должны иметь больше 3 знаков после запятой. В этом случае можно ввести одинаковый коэффициент масштабирования для всех чисел и учесть его при получении результата. К такого типа задачам можно отнести и задачи по подсчету изделий, количество которых всегда выражается в целых числах и т.п.

Достоинством представления чисел с фиксированной запятой является естественность этого способа и, как следствие, все действия с числами выполняются по правилам обычной арифметики, что повышает быстродействие машин. К недостаткам следует отнес­ти сравнительно узкий диапазон используемых чисел (этот недос­таток преодолевается, если использовать способ представления чисел с плававшей запятой).

Все арифметические действия в ЭВМ могут быть сведены к сло­жению чисел и их сдвигам в разрядной сетке.

Операция вычитания в ЭВМ заменяется сложением специально построенных кодов чисел: обратного и дополнительного. Кроме обратного и дополнительного существует и прямой код, который используется для представления отрицательных чисел в цифровых устройствах, если другие коды не применяются. Рассмотрим правила построения этих кодов, переход от одного кода к другому на примере целых чисел. Сразу отметим, что изображение положи­тельных чисел во всех кодах совпадает и старший бит (разряд) числа в любом коде отводится под знак.

Прямой код. Число X в прямом коде обозначается _. Строится прямой код по следующему правилу:

если , то

если , то

где - двоичные цифры.

Пример: а) X = +10110101 = 010110101

б) X = -10110101 =110110101.

Следовательно, прямой код двоичного числа совпадает по изобра­жению с записью данного числа, но в знаковом разряде ставится 0, если число положительное, и 1 - если число отрицательное.

Обратный код. Число X в обратном коде записывается как _. Если X > 0, то . Обратный код отри­цательного числа формируется по следующему правилу: в знаковый разряд числа записывается единица, а цифровые разряды инверти­руются, т.е. единица замещаются нулями, а нули единицами.

Если , то

Пример: а) X = +01011011 =001011011

б) X = -01011011 =110100100.

Дополнительный код. Если X > 0, то . Для отрицательных чисел дополнительный код получают по следую­щему правилу: числа переводят в обратный код и в его младший разряд прибавляют единицу. Если , то

Пример: а) X = +010101 = 0010101,

б) X = -010101 = 1101010+0000001=1101011.

Сложение чисел в ЭВМ с учетом знака состоит из следую­щих этапов:

1. Преобразование прямого кода исходных чисел в обратный или дополнительный код.

2. Поразрядное сложение кодов по правилам двоичной арифметики.

3. Преобразование полученного результата в прямой код при по­сылке в другие устройства машины.

Рассмотрим сложение чисел в ЭВМ с фиксированной запятой.

Сложение чисел в обратном коде. Обратные коды чисел суммируются поразрядно, причем знаковые разряды складываются также как разряды чисел. Если при сложе­нии в знаковом разряде возникает единица переноса, она прибав­ляется к младшему разряду суммы (эта операция называется цикли­ческим переносом).

Рассмотрим четыре возможных варианта.

1. Х>0, Y>0, X +Y >0.

В этом случае сложение выполняется в прямом коде, т.к. он совпадает с обратным.

2. Х>0, Y <0, X+Y <0.

Рассмотрим пример, в котором результат получим дважды: с помощью ручного счета, а затем выполним сложение так, как делает это машина в обратном коде (машинный счет). Ручной счет выполняется по правилам обычной арифметической логики.

Переведем результат в прямой код

Результат ручного и машинного счета совпадает. Здесь цикличес­кий перенос не возникает.

3. Х>0, Y <0, X+Y > 0.

Результат ручного и машинного счета совпадает. Здесь образуется циклический перенос: единица переноса, возникшая в знаковом разряде, прибавляется к младшему разряду суммы обрат­ных кодов.

4. Х<0, Y <0, X+Y < 0

Результат, переведенный в прямой код, совпадает с ручным счетом:

Сложение чисел в дополнительном коде производится так же, как и в обратном, но единица переноса, возникающая в знаковом разряде, отбрасывается. В качестве примера рас­смотрим сложение чисел в дополнительном коде.

1. X >0, Y < 0, X+Y < 0

Переход от дополнительного кода к двоичному числу выполняется по следующим правилам:

1) число, представленное в дополнительном коде, инверти­руется;

2) к полученному результату прибавляется единица в млад­ший разряд;

3) число, стоящее в знаковом разряде (0 или 1), определит знак результата.

Такой переход выполняется только для отрицательных чи­сел. Переведем результат в прямой код.

2. Х>0, Y <0, X+Y > 0.

3. X<0, Y<0, X+Y<0

Преобразуем полученный результат в прямой код:

Недостатком обратного и дополнительного кодов, имеющих один знаковый разряд, является то, что машина не всегда фиксирует переполнение разрядной сетки, если при неправильно подобран­ном масштабе результат выходит за границы разрядной сетки. Например:

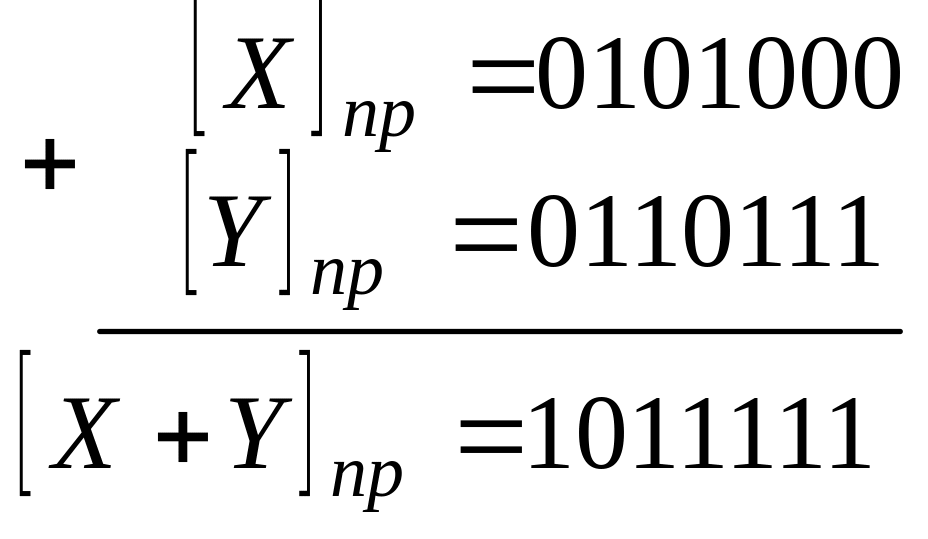
В этом случае, несмотря на то, что результат сложения двух положительных чисел должен быть также положительным, машина вос­примет результат как отрицательное число. Поэтому для обнаружения переполнения разрядной сетки был введен модифицированный обратный и дополнительный код, отличающийся от обычных обратно­го и дополнительного кода, наличием двух знаковых разрядов.

Число в модифицированном обратном коде записывается сле­дующим образом:

а) положительное число →

б) отрицательное число →

Любая другая комбинация чисел в знаковых разрядах (01 или 10) будет означать переполнение разрядной сетки. Решим приведенный выше пример в модифицированном обратном коде:

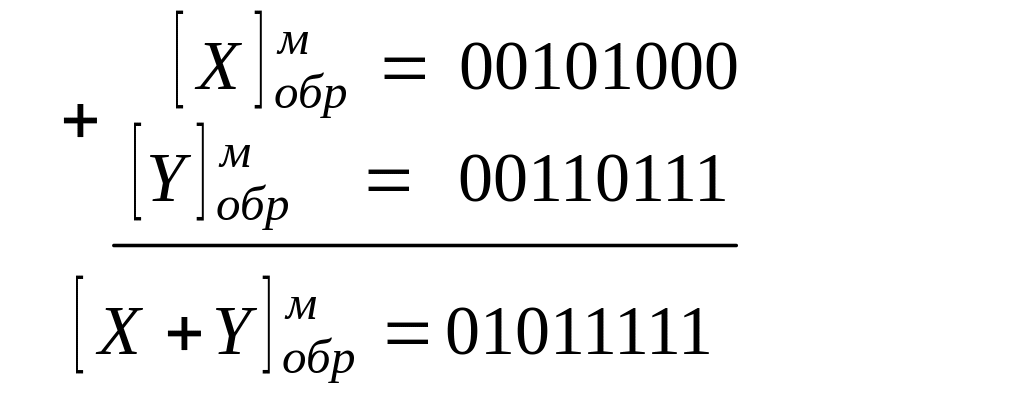
В машине оба знаковых разряда сравниваются, и при появлении приз­нака переполнения машина останавливается.

Число в модифицированном дополнительном коде записывается следующим образом:

а) положительные числа →

б) отрицательные числа →

Сложение чисел в модифицированном дополнительном коде происходит также как и в модифицированном обратном коде, но едини­ца переноса, образующаяся при сложении знаковых разрядов, отбрасывается.

Пример: X = 110101, Y = -001110

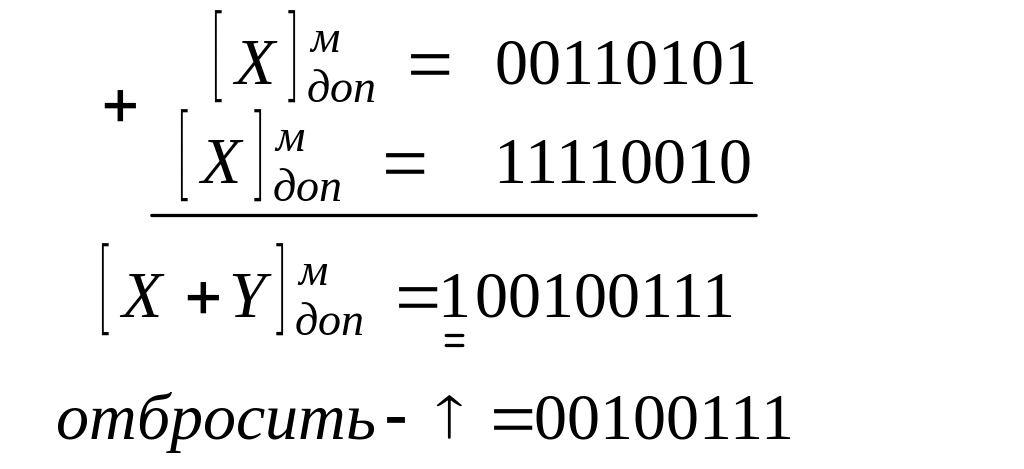
Вычитание двоичных чисел в ЭВМ заменяется сложением с вычитаемым, взятым с обратным знаком.

Ввиду того, что сумматор К155ИМ3, используемый в работе, четырехразрядный, то при использовании его для суммирования чисел с учетом их знака в обратном и дополнительном кодах старший разряд сделаем знаковым, а в оставшиеся три разряда будем записывать слагаемые. Таким образом, при выполнении практических заданий вы будете оперировать с трехразрядными целыми двоичными числами. Заполните таблицу 3, переведя положительные и отрицательные числа от 0 до 7 в прямой, обратный и дополни­тельный коды.

Чтобы использовать сумматор для вычитания двоичных чисел в обратном коде, его необходимо дополнить инверторами, преобразующими вычитаемое число в обратный код и обеспечить суммирование единицы переноса, если она возникает в знаковом разряде с содержимым самого младшего разряда. Принципиальная схема такого 4^х разрядного сумматора дана на рис.7.

Инверторы преобразуют вычитаемое в обратный код, а объединение выхода переноса SM4 ( ) со входом переноса SM1 ( ), так называемый циклический перенос, позволяет прибавить единицу переноса к самому младшему разряду.

Таблица 3

Десятичное число	Двоичное число	Прямой код	Обратный код	Дополнительный код
+7	0111	0111	0111	0111
+6
+5
+4
+3
+2
+1
0
–1
–2
–3
–4
–5
–6
–7

Чтобы схему, изображенную на рис. 7 можно было использовать и для суммирования, необходимо исключить из нее 4 инвертора. Следовательно, в сумматоре-вычитателе должна быть цепь управления, которая разрешала бы переходить от суммирования к вычи­танию и наоборот. Одна из таких функциональных схем сумматора-вычитателя показана на рис. 8. Вместо инверторов в ней использованы ЛЭ "исключающее ИЛИ". Если на один из входов ЛЭ "исключаю­щее ИЛИ" подать нуль, то информационные сигналы, поступающие на вторые входы, не инвертируются, т.е. информационный сигнал на выходе "исключающего ИЛИ" совпадает с информационным сигналом на входе. Поэтому суммирование осуществляется при нулевом управляющем сигнале. Если управляющий сигнал будет 1, то "исключающие ИЛИ" инвертируют вычитаемое и в этом режиме схема работает как вычитатель, вычитая двоичное число из двоичного числа .

Рассмотрим схему сумматора-вычитателя, работающего в допол­нительном коде (рис.9). Она отличается от схемы сумматора-вычитателя, работающего в обратном коде, во-первых, отсутствием цик­лического переноса, во-вторых, тем, что вход переноса CMP ( ) подключен к шине, задающей режим работы ("сложение" или "вычи­тание"). Режим сложения задается подачей на вход управляющей ши­ны уровня логического 0. При этом сигнале поступают на входы сумматора-вычитателя без инвертирования, а на входе пе­реноса сумматора СМР устанавливается нулевой уровень. Таким об­разом, сумматор-вычитатель работает как обычный сумматор, но пе­ренос, образующийся на выходе сумматора ССР отбрасывается.

При выполнении операции вычитания на вход управляющей шины подается уровень логической 1. В этом случае ЛЭ "исключающее ИЛИ" инвертируют дополнительный код положительного числа вычитаемого, поступающего на входы В, преобразуя слагаемое в обрат­ный код, а прибавление 1, появившейся на входе переноса сумматора СМР ( ) превращает обратный код в дополнительный код отрицатель­ного числа. Затем происходит суммирование дополнительных кодов чисел А и В, результат выдается в дополнительном коде.