Определение теоретического значения коэффициента Пуассона

Из молекулярно - кинетической теории известно, что внутренняя энергия одного мо­ля равна

где i - число степеней свободы данного газа. Число степеней свободы определяет число независимых координат, полностью описывающих положение молекулы газа в пространстве. Для идеального одноатомного газа необходимы три координаты, опи­сывающие поступательное движение такой молекулы в пространстве. Следовательно ему приписывают три степени свободы.

Молекула двухатомного идеального газа рассматривается как совокупность двух материальных точек-атомов, жестко связанных недеформируемой связью. Эта система кроме трех степеней свободы поступательного движения имеет еще две сте­пени свободы вращательного движения. Таким образом, двухатомный идеальный газ обладает пятью степенями свободы. Трехатомные и многоатомные нелинейные моле­кулы имеют шесть степеней свободы: три поступательных и три вращательных. Есте­ственно, что жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения.

подставляя это выражение в (4)

получим

(10)

С учетом (10) выражение (7) примет вид

(11)

С учетом (10) и (11) получим теоретическое значение коэффициента Пуассона

(12)

II. Теория метода и описание установки

Величину γ можно определить с помощью установки (рис.1),

с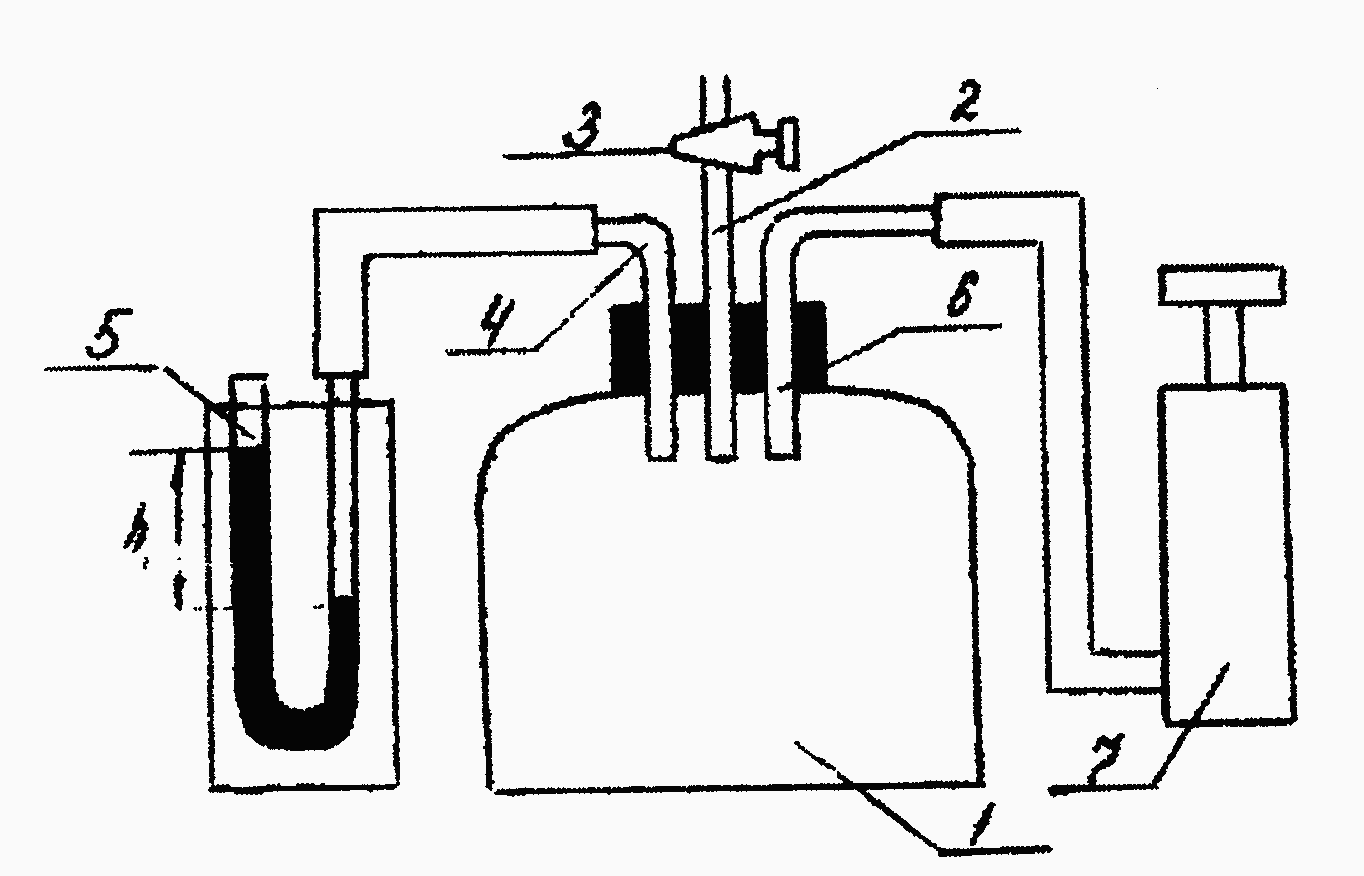 остоящей из стеклянного баллона 1,герметично зарытого пробкой, через пробку в баллон пропущена трубка 2, на верхнем конце которой имеется кран 3, соединяющий полость баллона с атмосферой. Через трубку 4, пропущенную через пробку в баллон, полость баллона соединяется с V-образным манометром 5. Через трубку 6 полость баллона соединяется с насосом 7.

Рис.1

В баллон при закрытом кране накачивается воздух. Давление воздуха в баллоне повысится и станет равным

где h₁ - избыток давления воздуха в баллоне над атмосферным давлением Н. Величи­на h₁ измеряется манометром. Открывают на короткое время кран 3, чтобы давление в баллоне сравнялось с атмосферным (р₂ ⁼ Н ), после чего закрывают кран.

Пусть масса воздуха поcле накачивания насосом в сосуде объемом V равна m. При открывании крана часть воздуха выходит. Обозначим массу вышедшего воздуха через Δm, тогда масса оставшегося воздуха

Масса воздуха m₁, которая заключается в объеме V, занимала перед открытием крана меньший объем Vi. Так как процесс кратковременный и заметного теплообмена между газом и стенками баллона нет, то его можно считать адиабатическим. Соглас­но уравнению Пуассона (для массы газа равной m₁) получим

(13)

Вследствие адиабатического расширения температура газа понизилась, а затем в результате теплообмена, температура его через небольшой промежуток времени станет равной комнатной. При этом давление газа поднимается до величины

Начальное и конечное состояние газа наблюдается при одинаковой температу­ре. Поэтому на основании закона Бойля-Мариотта получим

(14)

Решая уравнения (13) и (14) относительно у, получим

(15)

Разложим lg p₁ или lg p₃ в ряд Тейлора, ограничившись в этом случае двумя первыми членами:

Подставляя эти значения в формулу (15), получим окончательно

. (16)