4.1. Анализ конструкции

Стенки с ячейками, работающими под давлением, состоят из материала с очень высоким пределом прочности на разрыв по отношению к массе, например, боро- или кевларо-полиэтиленовый композит с толщиной, способной удерживать давление в ячейках с подходящим коэффициентом запаса в соответствии с инженерной практикой. Воздух или газ используется, чтобы создать давление в ячейках, используя связанную систему труб, такую, что в ячейки может подаваться давление время от времени. При обычных условиях у поверхности атмосферный воздух имеет плотность . Для сосуда под давлением изменение давление с высотой можно вывести при помощи компенсации силы тяжести на единицу площади части воздуха как , где - ускорение свободного падения ( на Земле), - плотность газа, - давление и - высота. При атмосферном давлении поведение газа может описываться при помощи закона идеального газа как , где - универсальная газовая постоянная, - молярная масса газа и - температура по Кельвину. Предполагая постоянной температуру ячейки и рассматривая гравитацию как постоянную по высоте, мы интегрируем, чтобы получить давление на вершине ячейки на высоте как:

(1)

где и является величиной высоты газового столба и является давлением у основания. Для земной атмосферы . Грузоподъёмность в килограммах вертикального цилиндра длиной и диаметром , который не имеет конструктивных усилий под давлением, является следующей

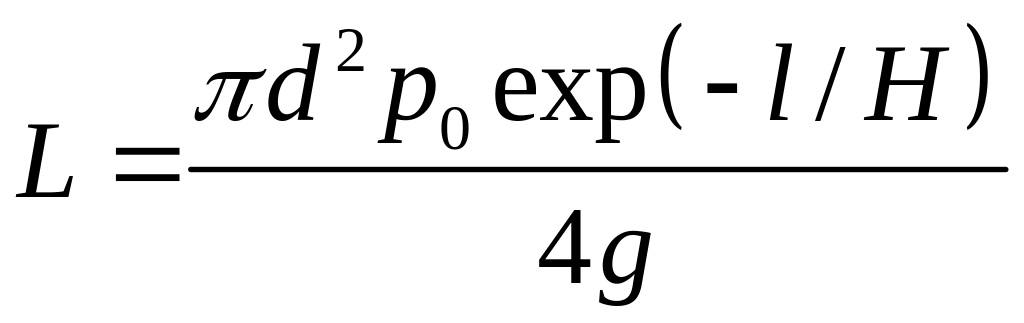. (2)

Предполагая случай конструкции из простой одиночной ячейки, масса такого сегмента получается как

. (3)

Если сегмент находится в непосредственном контакте с землёй, аппарат должен поддерживать только эту массу конструкции, поскольку масса сжатого газа может поддерживаться, начиная с основания. Если сегмент наращивает вверх конструкцию, поддерживаемая конструкция должна поддерживать массу сегмента и массу сжатого газа, которая получается как:

(4)

где - плотность газа при давлении в 1 атм. и - давление газа у основания в барах. Это выражение также может использоваться для подсчёта поднимаемой массы, которая обеспечивает некоторую поддержку для внутренней конструкции. Центр тяжести поддерживающего газа получается при помощи:

. (5)

Могут использоваться другие газы с более низкими молекулярными массами, чем у воздуха. Преимущества массы других создающих давление газов может быть приблизительно выражено при помощи отношения их молекулярной массы к молекулярной массе газообразного азота (главное составляющее атмосферного воздуха). Таким образом, конструкция, заполненная водородом, будет требовать 28/2=14 раз меньше массы газа и с гелием 28/4=7 раз меньше.

Сила, требуемая, чтобы сгибать простой столб, подобный лифту конструкции Б под нагрузкой, получается как:

, (6)

где - эффективная длина столба, зависящая от граничных условий столба, - эффективный модуль Юнга тонкостенного столба, где внутренняя конструкция поддерживается давлением и - момент инерции площади поперечного сечения. Предполагая, что внутренняя конструкция лифта зафиксирована у основания и гироскопически придавлена сверху, имеем . Для тонкостенного цилиндра круглого сечения, , где - толщина и - радиус.

Рассматривается пример внутренней конструкции, сконструированной для наземного лифта, чтобы получить доступ в околокосмическое пространство на высоте 20 км. Преимущественно, чтобы достичь орбиты, лифт может быть построен на высоте 5 км в одной из четырёх областей на экваторе. Внутренняя конструкция потребуется, чтобы перекрыть следующие 15 км до 20 км высоты. Основанная на лифте Б, подходящая конструкция содержит газовые ячейки с постоянной толщиной стенки 1,2 см, выполненной в виде тора с внутренним диаметром 228 м и наружным диаметром 230 м. Сделанный из бора, 15-тикилометровая конструкция лифта может поддерживаться при помощи газообразного водорода под давлением 150 бар. Рассматривая приближённо конструкцию как два концентрических цилиндра, имеем массу конструкции и массу требуемого газа для создания давления . Другие внутренние конструкции могут быть проанализированы путём сравнения с двухцилиндрической конструкцией и путём соответствующего согласования количества используемого материала для стенок.

Построенная на высоте 5 км, конструкция будет иметь поднимаемую массу , дающую общую массу . Грузоподъёмность конструкции в превышение требуемой для самоподдержки, составляет в силовом эквиваленте. Критическая изгибающая нагрузка на вершине составляет , в центре тяжести (расположенном на 7,3 км высоты внутренней конструкции) критическая нагрузка составляет , которая значительно превышает вес конструкции здания, включая массу газа, показывающего, что внутренняя конструкция будет устойчива и способна поддерживать поднимающуюся полезную нагрузку массой до . При помощи дальнейшего изменения толщины стенки, дальнейший предел конструкции может быть получен путём снижения центра тяжести и снижения массы конструкции, и более высокие конструкции могут быть построены. Напротив, диаметры внутренней конструкции могут быть изменены, чтобы увеличить жёсткость конструкции в основании, хотя изменение диаметра внутренней конструкции может быть нежелательной для установки оборудования лифта. Вдобавок к этому, внутренняя конструкция может быть сегментирована и соответствующе снабжена давлением без возникновения неуравновешенности поддерживающих сил между стенками сегмента. Перспектива использования пневматических балок требует экспериментального исследования, для того чтобы проверить теоретические предположения. Жу, Сет и Квин (2008) проверяют теоретические предположения, сравнив с экспериментом для наполненных газом консольных балок круглого сечения [9]. Работа по выполнению многобалочных конструкций ещё предстоит.