Лабораторная работа № 2

Переходные процессы в RLC цепях.

1. Общие сведения

Л

а б

Рис. 1. Линейные цепи второго порядка: а – последовательный резонансный контур; б – параллельный резонансный контур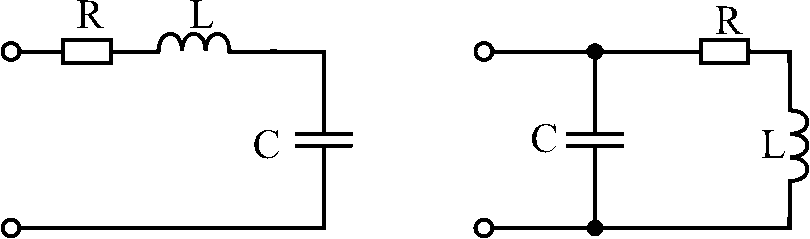

инейные цепи 2-го порядка содержат два разнотипных реактивных элемента L и C. Примерами таких цепей являются последовательный и параллельный резонансные контуры (рис.1). Переходные процессы в колебательных контурах описываются дифференциальными уравнениями 2-го порядка. Рассмотрим случай разряда емкости на RL цепь (рис.2). Составим уравнение цепи по первому закону Кирхгофа:

, (1)

где

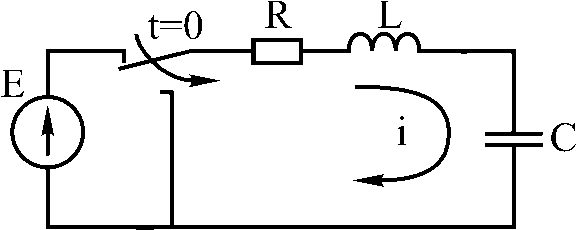
П

Рис. 2. Включение RLC цепи на постоянное напряжение

осле дифференцирования (1) получим

. (2)

Решение U_с(t) уравнения (2) находим как сумму свободной U_св(t) и принужденной U_пр составляющих

U_с=U_св+U_пр. (3)

U_пр зависит от Е, а U_св(t) определяется решением однородного дифференциального уравнения вида

. (4)

Характеристическое уравнение для (4) имеет вид

LCp² + RCp + 1 = 0, (5)

Корни характеристического уравнения

.

Величину R/2L = α называют коэффициентом затухания, – резонансной частотой контура. При этом

.

Характер переходных процессов в контуре зависит от вида корней p₁ и p₂. Они могут быть:

1) вещественные, различные при R > 2ρ, Q < 0,5;

2) вещественные и равные при R = 2ρ, Q = 0,5;

3) комплексно-сопряженные при R < 2ρ, Q > 0,5.

Здесь – характеристическое сопротивление, Q = ρ/R – добротность контура.

В схеме рис. 2 до коммутации при t<0 емкость заряжена до напряжения U_c(0_-) = E. После коммутации емкость начинает разряжаться и в контуре возникает переходный процесс. В случае 1 при Q < 0,5 решение уравнения (2) имеет вид

(6)

Для нахождения постоянных интегрирования А₁ и А₂ запишем выражение для тока в цепи

.

Используя начальные условия U_c(0_-) = E и i(0_-) = 0, получаем систему уравнений

(7)

Из решения системы имеем

.

В результате для тока и напряжений в контуре получим

В

Рис. 3. Диаграммы изменения тока и напряжений в контуре при Q < 0,5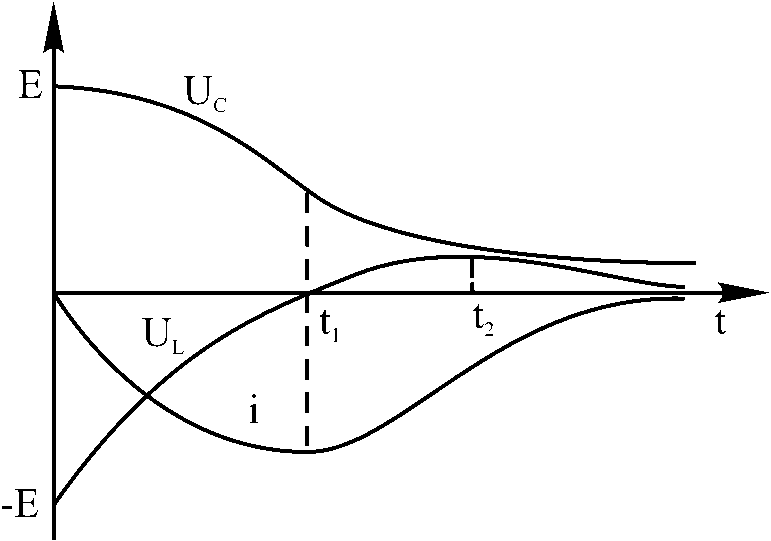

ременные диаграммы тока и напряжений показаны на рис. 3. Величины U_c, i, U_L состоят из двух слагаемых, затухающих по экспоненциальному закону с постоянными времени , . Момент времени соответствует максимуму тока и нулевому значению напряжения U_L. При низкой добротности Q < 0,5 в контуре происходит апериодический разряд емкости. На интервале 0–t₁ энергия конденсатора W_c=E²C/2 расходуется частично на создание магнитного поля индуктивности и частично на потери в сопротивлении R. При t > t₁ энергия конденсатора и индуктивности расходуется в резисторе R.

В случае Q > 0,5 корни характеристического уравнения (5) комплексные, сопряженные:

,

где – частота собственных затухающих колебаний контура. Решение дифференциального уравнения (2) для этого случая имеет вид

. (8)

Закон изменения тока

. (9)

Постоянные интегрирования А и  определяются из начальных условий для U_c и i и законов коммутации

Решая систему уравнений, находим

.

Окончательно имеем

(10)

Согласно (10) в контуре имеет место колебательный разряд емкости с частотой ω_с. Интервал T_c=2π/ω называется квазипериодом. Временные диаграммы изображены на рис.4. При Q>>1,  ≈ 90 напряжения на емкости и индуктивности противофазные: U_c(t)=-U_L(t). Колебательный процесс имеет затухающий характер из-за потерь в контуре на сопротивлении R. Затухание колебаний происходит по экспоненциальному закону со скоростью, зависящей от коэффициента α=R/2L. Для оценки скорости затухания используют декремент затухания

Затухание колебаний происходит тем быстрее, чем больше сопротивление R. При R=2ρ колебательный процесс переходит в апериодический. При колебательном разряде происходит

Рис. 4. Колебательный переходный процесс в RLC контуре.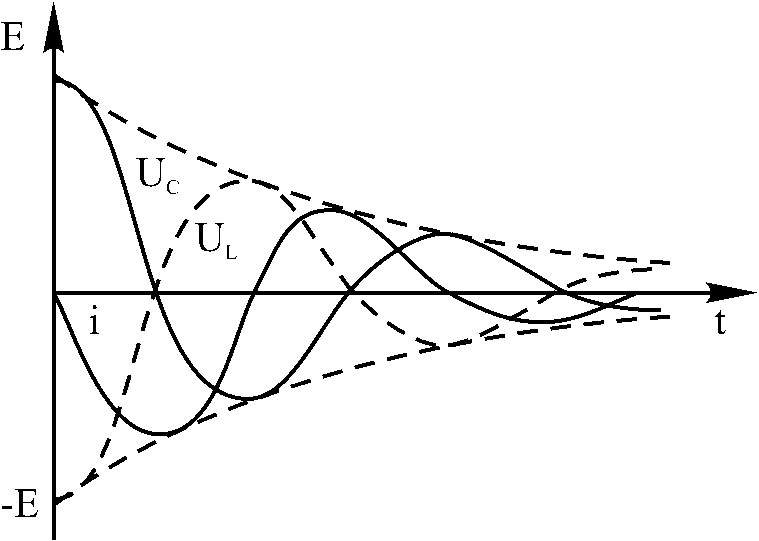

попеременный обмен энергией между емкостью и индуктивностью, энергия электрического поля переходит в энергию магнитного поля и наоборот. Часть энергии теряется в резисторе и процесс постепенно затухает. При R=0 колебания оказываются незатухающими с частотой . Такой колебательный контур называется без потерь.

Случай Q=0,5 является пограничным между апериодическим и колебательным процессами. При R=2ρ р₁=р₂=р=-α и выражение для тока и напряжений в контуре имеют вид

Значение R=2ρ называется критическим сопротивлением контура.