4.5 Метод Рунге – Кутта 4-го порядка
Пусть дано дифференциальное уравнение первого порядка
с начальным условием
y(x0) = y0.
В
ыберем
шаг h и введём обозначения:
xi = x0 + i.h и yi = y(xi) , где i = 0, 1, 2, … .
Аналогично описанным выше методам производится решение дифференциального уравнения. Отличие состоит в делении шага на 4 части.
Согласно методу Рунге – Кутта четвёртого порядка, последовательные значения yi искомой функции y определяются по формуле:
где
, i
= 0, 1, 2, …
а числа k1(i), k2(i), k3(i), k4(i) на каждом шаге вычисляются по формулам:
Это явный четырёхэтапный метод четвёртого порядка точности.
Методы Рунге – Кутта легко программируются и обладают значительной точностью и устойчивостью для широкого круга задач.
На рисунке 6 приведена блок-схема процедуры RUNGE(X0, XK, Y0, N, Y) для решения задачи Коши описанным выше методом Рунге – Кутта.
RUNGE4(X0, XK, Y0, N, Y)
h
F(x,
y)
– заданная функция – должна быть
описана отдельно.
Входные
параметры:
X0,
XK
– начальное и конечное значения
независимой переменной;
Y0
– значение y0
из начального условия y(x0)
= y0;
N
– количество отрезков разбиения;
Выходные
параметры:
Y
– массив значений искомого решения в
узлах сетки;
i = 0, … , N-1
x = X0 + i * h
K1 = h * F(x, Yi)
K2 = h * F(x + h/2, Yi + K1 / 2)
K3 = h * F(x + h/2, Yi + K2 / 2)
K4 = h * F(x + h, Yi + K3)
K = (K1 + 2*K2 + 2*K3 + K4) / 6
Yi+1 = Yi + K
End
Рисунок 6. Блок-схема процедуры RUNGE
На рисунке 7 приведена блок-схема алгоритма основной программы для решения задачи Коши и получения результатов с фиксированным количеством отрезков разбиения N. В основной программе происходит обращение к процедуре RUNGE(X0, XK, Y0, N, Y), вычисляющей значения искомой функции yj в точках xj методом Рунге – Кутта.
Исходными данными в данной задаче являются:
X0, XK – начальное и конечное значения независимой переменной;
Y0 – значение y0 из начального условия y(x0) = y0;
N – количество отрезков разбиения.
Результаты работы программы выводятся в виде двух столбцов:
X – массив значений узлов сетки;
Y – массив значений искомого решения в соответствующих узлах сетки.
В
вод
X0, XK, Y0, N
R
UNGE(X0,
XK, Y0, N, Y)
h = (XK – X0) / N
i
= 0 … N
X = X0 + i * h
В
ывод
X, Yi
E
nd
Рисунок 7. Блок-схема алгоритма основной программы для решения задачи Коши с фиксированным количеством отрезков разбиения N
4.6 Решение дифференциальных уравнений в среде MathCad
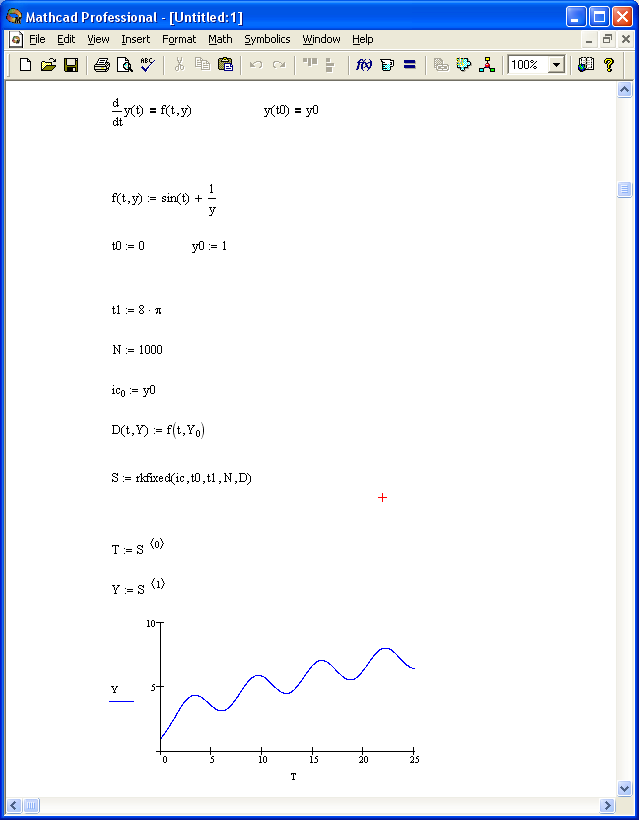
Рисунок 8. Пример решения дифференциального уравнения методом Рунге-Кутта 4 порядка в среде MathCad.
Задания
РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ 1–го ПОРЯДКА С ФИКСИРОВАННЫМ ШАГОМ
В курсовой работе необходимо указанными методами решить задачу Коши для дифференциального уравнения 1 – го порядка на отрезке [ Хо, Хк] с шагом h и начальным условием У(Хо)=Уо.
Ответ должен быть получен в виде таблицы результатов:
X |
Y(1) |
Y(2) |
Y(T) |
X0 |
Y0(1) |
Y0(2) |
Y(X0) |
X1 |
Y1(1) |
Y1(2) |
Y(X1) |
… |
… |
… |
… |
Xk |
Yk(1) |
Yk(2) |
Y(Xk) |
где : Y (1), Y (2) - решения, полученные различными численными методами, Y(T) – точное решение дифференциального уравнения.
Возможно представление результатов решения не в виде таблицы, а в виде списков.
Данные таблицы визуализировать на форме в виде графиков.
Исходные данные для различных вариантов представлены в таблице.
Перед вычислением последнего столбца таблицы результатов необходимо из начальных условий вычислить значение коэффициента с, используемое в общем решении.
Таблица - Задания для курсовых работ.
№ |
Дифференциальные уравнения |
X0 |
Xk |
h |
Y0 |
Общее решение |
Методы решения |
1 |
xydx+(x+1) dy=0 |
1.2 |
2 |
0.1 |
1 |
y=c(x+1) exp(-x) |
Эйлер, Рунге-Кутт |
2 |
y=xy 2+2xy |
0 |
2 |
0.2 |
-1.8 |
y=-2/(1+cexp(-x2)) |
Эйлер, Эйлер модифицированный |
3 |
y=2 |
1 |
2 |
0.1 |
16 |
y=(xln(x)-x+c) 2 |
Рунге-Кутт, Эйлер модифицированный |
4 |
yctg(x)=2-y |
0 |
1 |
0.1 |
1 |
y=2-cos(x) |
Эйлер, Рунге-Кутт |
5 |
yx=3y |
1 |
1.4 |
0.05 |
2 |
y=cx 3 |
Эйлер, Эйлер модифицированный |
6 |
yy+x=1 |
0 |
1 |
0.1 |
2 |
y= |
Рунге-Кутт, Эйлер модифицированный |
7 |
y=-0.05y |
1 |
2 |
0.1 |
2 |
y=cexp(-0.05•x) |
Эйлер, Рунге-Кутт |
8 |
y=4x-2y |
1.2 |
2 |
0.1 |
2.4 |
y=cexp(-2x)+2x-1 |
Эйлер, Эйлер модифицированный |
9 |
(y2-2xy)dx+x2dy =0 |
1 |
2 |
0.1 |
0.2 |
y=x2/(c+x) |
Рунге-Кутт, Эйлер модифицированный |
10 |
(y-y) x=e x |
1 |
2 |
0.1 |
4 |
y=exp(x)(lnx+c) |
Эйлер, Рунге-Кутт |
11 |
yx=exp(x)-y |
1.0 |
2 |
0.1 |
1 |
y=[exp(x)+1-e]/x |
Эйлер, Эйлер модифицированный |
12 |
yx=4y |
1 |
1.4 |
0.05 |
2 |
y=x4c |
Рунге-Кутт, Эйлер модифицированный |
13 |
y(x+1)=y + 2 |
0 |
0.8 |
0.1 |
0 |
y=(x+1) c-2 |
Эйлер, Рунге-Кутт |
14 |
2xydx-(x+1)dy=0 |
0 |
0.8 |
0.05 |
4 |
y=e2x c/(x+1)2 |
Эйлер, Эйлер модифицированный |
15 |
y+2xy=xexp(-x 2) |
0 |
1 |
0.1 |
1 |
y=exp(-x 2)(c+x 2/2) |
Рунге-Кутт, Эйлер модифицированный |
16 |
y+y=cos(x) |
0 |
/2 |
/10 |
1 |
y=cexp(-x)+[cos (x)+ +sin (x)] /2 |
Эйлер, Рунге-Кутт |
17 |
yx=y+1 |
1 |
5 |
0.5 |
-0.9 |
y=cx-1 |
Эйлер, Эйлер модифицированный |
18 |
3x2 – y=0 |
1 |
1.8 |
0.1 |
0 |
y=x3-c |
Рунге-Кутт, Эйлер модифицированный |
19 |
xy+y=y 2ln(x) |
1 |
1.6 |
0.1 |
4 |
y=[1+ln (x)+cx]-1 |
Эйлер, Рунге-Кутт |
20 |
(1+x 2)dy+ydx=0 |
1 |
1.8 |
0.1 |
1 |
lny=-arctg(x)+c |
Эйлер, Эйлер модифицированный |
21 |
y=y/x+sin(y/x) |
1 |
1.5 |
0.05 |
/2 |
y=2xarctg(cx) |
Рунге-Кутт, Эйлер модифицированный |
22 |
xy-y=x 2cos(x) |
1.8 |
2.4 |
0.1 |
0.5 |
y=x[sin(x)+c] |
Эйлер, Рунге-Кутт |
23 |
y+y/x=3/x |
1 |
1.8 |
0.1 |
0 |
y=3(x-1)/x |
Эйлер, Эйлер модифицированный |
24 |
y=2x2+2y |
0 |
1 |
0.1 |
1 |
y=1.5exp(2x)-x2-x-c |
Рунге-Кутт, Эйлер модифицированный |
25 |
ysin(x)-ycos (x)=0 |
/2 |
3/4 |
/20 |
1 |
y=sin (x) |
Эйлер, Рунге-Кутт |
26 |
(1+y 2) dx=xdy |
1 |
1.5 |
0.05 |
1 |
y=tg( ln (cx) ) |
Эйлер, Эйлер модифицированный |
27 |
(x-y) dx+xdy=0 |
1.2 |
2 |
0.1 |
2 |
y=x(c-ln (x)) |
Рунге-Кутт, Эйлер модифицированный |
28 |
xy=y [ln (y)-ln (x)] |
1 |
2 |
0.1 |
1 |
y=xexp(1+cx) |
Эйлер, Рунге-Кутт |
29 |
x 2+xy=y |
1 |
1.4 |
0.05 |
0 |
y=x-x 2 |
Эйлер, Эйлер модифицированный |
30 |
y+2xy=2xy 2 |
1 |
1.2 |
0.02 |
2 |
y=[(1+cexp(x 2)]-1 |
Рунге-Кутт, Эйлер модифицированный |
ln(x)