3. Частные случаи уравнения Бесселя.

В математической физике наиболее часто встречаются функ­ции Бесселя

где п—целое число.

Первые две из этих функций представляются следующими рядами:

Для них имеются подробные таблицы. Графики функций J₀(x), J₁(x) и У₀(x) приведены на рис.1 и 2.

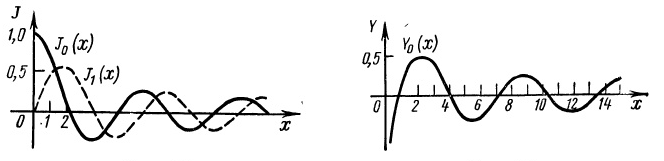
Рис.1 Рис.2

Из формулы (23) видно, что вычисление функций J₂(x), J₃(x) и т. д. сводится к вычислению соответствующих значении функций J₀(x) и J₁(x).

Обратимся теперь к функции J_n+1/2 (x), где n — целое число.

Найдем прежде всего значения функций J_1/2 (x) и J_-1/2 (x), для чего обратимся к разложению (14); из него видно, что

Но из формулы (11) непосредственно вытекает, что

Таким образом,

Последняя сумма представляет собой разложение sin x в степен­ной ряд, вследствие чего

Аналогично, из разложения (15) вытекает, что

Если теперь воспользоваться формулой (23), то нетрудно видеть, что

Вообще, функция Бесселя J_n+1/2 (x) при целом n выражается через элементарные функции, а именно:

где Р_n (1/x) — многочлен степени n относительно 1/x, а

Q_n-1 (1/x) —многочлен степени n—1, причем P_n(0) = 1, 0_n-1(0)=0. Отсюда следует, что при больших значениях х имеет место асимптотическое представление функции Бесселя:

где через О(x^-1) обозначена величина порядка 1/x.

Отметим, что асимптотическая формула (29) справедлива не только при =n+1/2, но и при всех значениях .

4. Ортогональность функций Бесселя и их корни.

Рассмотрим уравнение

где k — некоторая постоянная, отличная от нуля.

Введем вместо x новую независимую переменную t = kx. Тогда уравнение (30) преобразуется в такое:

а это есть уравнение Бесселя. Следовательно, функция y=J_v (kx) будет решением уравнения

которое разделив на x, можем написать в виде

Возьмем два различных значения k и напишем соответствую­щие дифференциальные уравнения:

Умножая первое из этих равенств на J_v (k₂ x), а второе— на J_v (k₁ x) и вычитая одно из другого, после несложных преобразований получим:

Если теперь воспользоваться формулой (14), то нетрудно убе­диться, что выражение, стоящее здесь в квадратных скобках, может быть разложено по степеням x, причем наинизшая степень х будет х^2(v+1). Отсюда ясно, что это выражение будет обра­щаться в нуль при х = 0, если > —1. Приняв это во внима­ние, проинтегрируем равенство (32) по некоторому конечному промежутку (0, l); тогда получим

где через (') обозначается, как обычно, дифференцирование по аргументу. При l = 1 эта формула принимает вид:

Покажем теперь, что при >—1 функция Бесселя J_V(x) не может иметь комплексных корней. Допустим, что она имеет такой корень а+ib, причем а . В разложении (14) все коэффициен­ты разложения вещественны и, следовательно, функция J₁(x) кроме корня a+ib должна иметь и сопряженный корень a-ib. Обра­тимся к формуле (34) и положим k₁=a+ib и k₂=a+ib; при этом k₁²≠k₂² и формула дает

Величины J_V(k₁x) и J_V(k₂x) будут комплексно сопряженными, следовательно, в предыдущей формуле под знаком интеграла стоит положительная величина и эта формула не может иметь места.

Функция Бесселя J_v(x) не может иметь и чисто мнимых корней. Действительно, подставив ± ib в формулу (14), получим разло­жение, содержащее только положительные члены:

так как, согласно формуле (8), гамма-функция Г(x) принимает положительные значения при х > 0.

Покажем теперь, что функция J_v(x) имеет вещественные корни. Для этого обратимся к асимптотическому разложению функции Бесселя (29):

Из этой формулы видно, что при беспредельном удалении x: вдоль положительной части оси Ох второе слагаемое в квадратных скобках стремится к нулю, а первое — бесчисленное множество раз изменяется от -1 к +1. Отсюда непосредственно вытекает, что функция J_v(x) имеет бесчисленное множество вещественных корней.

Таким образом, приходим к следующему результату: если > -1, то функция J_v(x)имеет все корни вещественные.

Заметим, кроме того, что из разложения (14), содержащего только четные степени, непосредственно вытекает, что корни J_v(x) будут попарно одинаковыми по абсолютной величине и обратными по знаку, так что достаточно рассматривать только положитель­ные корни.

Пусть k₁= , k₂= , где µ_i и µ_l—два различных положи­тельных корня уравнения.

Тогда формула (33) дает непосредственно следующее свойство ортогональности функций Бесселя:

Пусть теперь k= , где µ— положительный корень уравнения (35). Возьмем формулу (33), в которой положим k₁=k₂, k₂ а будем считать переменным и стремящимся к k, тогда получим

При k₂- >правая часть этого равенства становится неопре­деленной так как числитель и знаменатель стремятся к нулю. Раскрыв эту неопределенность по правилу Лопиталя, получим

Положив в формуле (22) х=µ и приняв во внимание, что есть корень уравнения (35), получим

и формулу (37) можно записать еще следующим образом:

Таким образом, мы имеем

( > -1)

где µ_i и µ_j—положительные корни уравнения J_V(x)=0.

Рассмотрим теперь более общее уравнение

где α и β—заданные вещественные числа.