3.2 Базовые функции

Функция, которая определяет, как сильно форма кривой зависит от конкретной контрольной точки Qi (иначе - Bi), называется базовой функцией (basis function) этой контрольной точки.

Замечание. Собственно, в названии В-сплайнов буква "В" и означает "базовые" (basis).

Значение базовой функции есть вещественное число и описание NURBS-кривой требует задания базовой функции для каждой контрольной точки.

Пример. Можно описать значения функции для выбранного значения параметра t, например, таким образом: 30% положения одной контрольной точки плюс 60% – другой и плюс 10% – третьей. Это, в частности, означает, что когда движущаяся частица удаляется от некоторой контрольной точки, она испытывает все меньшее воздействие. И, наоборот, при приближении частицы к контрольной точке ее положение все больше от нее зависит.Такой эффект повторяется всякий раз, когда движущаяся частица проходит все контрольные точки.

Подобное "влияние" контрольной точки может быть не только выражено числовыми значениями, но и визуализировано на графике (это тоже функция). Можно построить график базовой функции как зависимость влияния некоторого параметра на движущуюся частицу, например в процентах, от значения 1 (рис. 1.6).

Максимальный эффект (максимальное влияние) достигается в совершенно определенной точке и постепенно уменьшается по мере удаления. Форма кривой, описывающей эту зависимость, напоминает колокол.

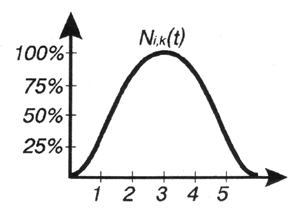Рис. 1.6. Типичный график базовой функции отдельной контрольной точки

Поскольку каждая контрольная точка "обязана" иметь свою базовую функцию, NURBS-кривая, построенная, например, по пяти контрольным точкам, должна иметь пять таких функций, перекрывающих некоторую область результирующей кривой (рис. 1.7).

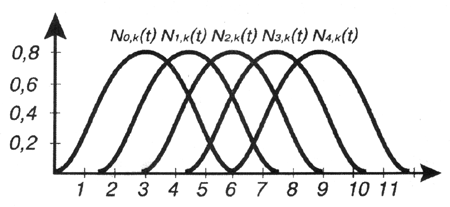Рис. 1.7. Однородные базовые функции для множества контрольных точек

3.3. Узлы. Характеристика семейства базовых функций.

На рис. 1.7 все базовые функции имеют одинаковую форму и размещены на равных расстояниях друг от друга. Это очень симметрично и элегантно, но для нас желательно варьировать длины интервалов таким образом, чтобы определенные контрольные точки влияли на значительно больший сегмент кривой, а определенные – на меньший. Это создает условие для неоднородности (Non-Uniform) в описании кривой.

Однако определение последовательности точек, на которые разбивается ось параметра t, задача не простая. Ведь при изменении относительных интервалов между такими точками, появляется возможность менять длительность воздействия контрольных точек на движущуюся вдоль кривой частицу.

Точки, разграничивающие интервалы, получили название узлов (knots), а их упорядоченный список – название узлового вектора (knot vector).

Узловой вектор базовой функции, представленный на рис. 1.8, имеет вид

{0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0}

Это пример однородного узлового вектора (uniform knot vector), в котором все функции определены на одинаковых временных интервалах.

Рис. 1.8. Пример однородного узлового вектора

Следующий рисунок (рис. 1.9) представляет пример кривой, созданной на основе такого узлового вектора.

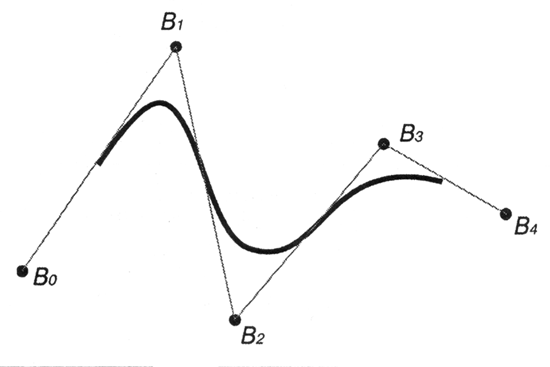Рис. 1.9. NURBS-кривая с однородным узловым вектором

Если изменить узловой вектор, например, так:

{0.0, 1.0, 2.0, 3.75, 4.0, 4.25, 6.0, 7.0}

то получится другое множество неоднородных (non-uniform) базовых функций (рис. 1.10) и, соответственно, другая форма кривой (рис. 1.11), которая строится на тех же контрольных точках, что и на рис. 1.9.

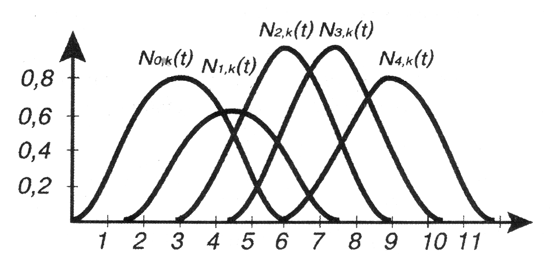Рис. 1.10. Неоднородные базовые функции для множества контрольных точек

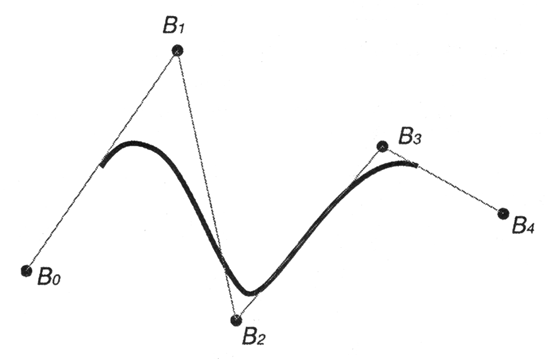Рис. 1.11. NURBS-кривая с неоднородным узловым вектором

Характеристика семейства базовых функций

Для любого значения параметра t сумма всех базовых функций строго равна 1.

Если веса всех контрольных точек положительны, кривая лежит в области, полученной соединением крайних (внешних) контрольных точек. Такой "габаритный" контейнер получил название "выпуклой оболочки" (convex hull).