Аморфні тіла

На відміну від кристалічних аморфні тіла повністю ізотропні, тобто їх властивості однакові в усіх напрямах.

• Аморфні тіла не мають певної температури плавлення. Якщо, наприклад, нагрівати скло, воно стає м’яким і тягучим.

• Друга їх характерна властивість – пластичність.

Залежно від характеру впливу (зокрема часу, протягом якого діє сила) аморфні речовини поводять себе або як крихкі тверді тіла, або як дуже в’язкі рідини.

Аморфний стан речовини нестійкий: через певний час аморфна речовина переходить у кристалічну.

Теплоємність кристалів.

К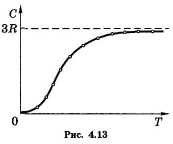 ласична модель. У основі класичної теорії теплоємності твердих тіл (кристалів) лежить закон рівнорозподілу енергії по ступенях свободи. Тверде тіло розглядають як систему N незалежних один від одного атомів, що мають по три коливальні ступені свободи. На кожну з них доводиться в середньому енергія kT (kT/2 у вигляді кінетичної і kT/2 у вигляді потенційної). Маючи на увазі, що число коливальних ступенів свободи рівне 3N, одержимо, що внутрішня енергія одного моля атомів U = 3N_AkT = 3RT. Звідси молярна теплоємність

C = U/T = 3R (4.35)

У цьому суть закону Дюлонга і Пті, який стверджує, що молярна теплоємність всіх хімічно простих твердих тіл однакова і рівна 3R. Цей закон виконується достатньо добре тільки при порівняно високих температурах. Дослід показує, що при низьких температурах теплоємність тіл убуває (рис. 4.13), прагнучи до нуля при Т  0 згідно із законом С  Т³.

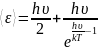(4.37)

Перший доданок тут - це так звана нульова енергія даного осцилятора. Вона не залежить від Т і не має відношення до теплового руху. Тому в теорії теплоємності тіл її можна опустити і вираз для внутрішньої енергії одного моля матиме вигляд:

U = 3N_A = 3N_A 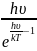(4.38)

Тепер можна знайти молярну теплоємність кристалічних решіток:

Цей вираз називають формулою Ейнштейна.

Модель Дебая. У цій моделі кристалічні грати розглядаються як зв'язана система взаємодіючих атомів. Коливання такої системи - результат накладення багатьох гармонійних коливань з різними частотами. Під гармонійним осцилятором тієї або іншої частоти. Задача зводиться до знаходження спектру частот цих осциляторів. Дебай звернув увагу на те, що при низьких температурах основний внесок в теплоємність вносять коливання (осцилятори) низьких частот, яким відповідають малі кванти енергії h. Практично тільки такі коливання і збуджені при низьких температурах. Низькочастотний же спектр коливань решіток може бути розрахований достатньо точно, і обчислення виявляються досить простими. З теорії виходило, що при Т  0 дійсне С  Т³.

де х_m = h_макс/kT = /T.

Вираз називають формулою Дебая.

Рідкі кристали.

Рідкокристалічним станом речовини називається такий стан, властивості якого є проміжними між властивостями твердого кристала і рідини. Згідно законам термодинаміки, агрегатні стани речовин підрозділяються на три види: тверде, рідке і газоподібне, проте таке розділення не відображає внутрішню будову речовини, ступінь впорядкованості його частинок. Деякі речовини (скло, смоли) володіють властивостями характерними і для твердих, і для дуже в'язких переохолоджених рідин. Зокрема, деякі органічні матеріали переходять з твердого стану в рідкий, випробовуючи ряд переходів, що включають утворення нової фази, яку називають рідкокристалічним станом (рідким кристалом).