2.5.2 Алгоритм формирования обратного кода. Арифметические и логические варианты алгоритмов.

Пусть прямой код операнда Х запишется как: X<0

[X]_пр. = 1, Х₁, Х₂,…, Х_i, …,Х_n (2.6)

Обратный код отрицательного операнда Х получают инверсией содержимого всех числовых разрядов

(логический алгоритм):

[Х]_обр. = 1, Х’₁, Х’₂, …, Х’_i, …, X’_n (2.7)

Для X_i = 1 инверсия равна: X’_I = 0

Для X_i = 0 инверсия равна: X’_I = 1

Для получения арифметического алгоритма образования обратного кода сложим, левые и правые части выражений

(2.6) и (2.7):

[X]_пр.+[X]_обр. = 10,11…1…1 = 11-1*10^-n

[Х]_обр. = Х, если Х>0

[Х]_обр. = Х – [X]_пр.-1*10^-n, для Х<0

Арифметический алгоритм образования обратного кода имеет вид:

[X]_обр. = Х, для Х≥0

[X]_обр. = 11-[X]_пр. – 1*10^-n, если Х<0

2.5.3 Сумматор обратных кодов (циклический сумматор), аксиомы обработки обратных кодов.

Аксиома 1: Сумма обратных кодов двух операндов X и Y эквивалентна (совпадает) обратному коду их суммы.

[X]_обр. + [Y]_обр. ≈ [X+Y]_обр.

Аксиома 2: Результат суммирования двух операндов на циклическом сумматоре получают в обратном коде, если он отрицательный и в прямом, если он положительный.

Если (X+Y)<0, то [X+Y]_обр.

Если (X+Y)≥0, то [X+Y]_пр.

Аксиома 3: Если при суммировании операндов │X│<1 и │Y│<1, образуется единица переноса из разряда знака ([X+Y]_зн.) эквивалентная P_зн.,

[X+Y]_зн. ≈ P_зн. 1*10^-n

то эта единица преобразуется в единицу младшего разряда и участвует в окончательном формировании результата как слагаемоее. Цепь, по которой происходит передача этой единицы, называется обратной связью и формируется в циклическом сумматоре.

2.5.4 Блок схема суммирования двоичной информации в форме с плавающей запятой

₁

начало

₂

Ввод мантисс операндов: m_x, m_y

Нормализация результата

конец

Запись в память

Нормализован ли результат операции?

[m_x]_доп. + [m_y]_доп.

Формирование инверсных кодов m_x и m_y

P_x-P_y

Денормализация m_x

Денормализация m_y

P_x>P_y

Ввод порядков операндов: P_x, P_y

P_y-P_x

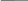
₃

Да ₄ Нет

_{5 6}

^{7 8}

₉

₁₀

Нет ¹¹ Да ¹²

₁₄

¹³

Реализация данного алгоритма после задания операндов в нормальной форме (Х= ±m_x*10^±Px; Y= ±m_y*10^±Py) требуют выравнивания порядков в сторону большего.

1/N≤|m|<1

X= 0,10010101*10¹⁰⁰¹

Y= -0,11001100*10¹¹⁰

P_x= 1001

-

P_y= 110

P_x-P_y= [11]₂=[3]₁₀

[m_x]_доп.= 010010101000

+ m_y= -0,00011001100

[m_y]_доп.= 111100110100

[m_x+m_y]_пр.= 0,01111011100

P_x+y=1001+1=1000

[m_x+m_y]_пр.=0,01111011100*10¹⁰⁰¹

X+Y = 0,11110111*10¹⁰⁰⁰