2.4 Алгоритмы обработки кодированной информации в арифметических устройствах.

Алгоритмы обработки арифметической информации используют специальные коды её представления для того, чтобы иметь на машинном уровне одно универсальное устройство для выполнения суммирования и вычитания кодов. Различают прямой и инверсные коды чисел. Прямой код служит для автоматического представления знака числа в микропроцессоре..

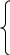
X, если x≥0

[X]_пр=

1-x, если x≤0

Ноль в прямом коде имеет два различных представления

Для x=+0, 0…0 [x]_пр=0, 0….0

Для x= - 0, 0…0 [x]_пр=1, 0….0-(-0, 0….0) = 1, 0…0

Для чисел представленных в форме с фиксированной запятой прямой код автоматически задаёт знак числа.

Именно в этом коде числа и могут быть размещены в памяти микропроцессора.

2.4.1 Логический алгоритм формирования дополнительного кода отрицательных чисел.

Логический алгоритм образования дополнительного кода отрицательного числа включает следующие шаги:

1. в разряд знака кода ставится 1 (т.к. число отрицательное);

2. все разряды числовой части инвертируются (т.е. 0 заменяется 1-й; а 1 заменяется на 0);

3. к младшему разряду кода прибавляют 1;

Пример: Х= -0,10111100

[Х]_доп.= 1 01000100

2.5 Аксиомы, сопровождающие суммирование дополнительных кодов.

1. Сумма дополнительных кодов двух операндов X и Y эквивалентна дополнительному коду их суммы , то-есть :[Х]_доп.+[Y]_доп. ≈ [X+Y]_доп.

2. Если при суммировании дополнительных кодов образуется единица переноса из разряда знака, то она не участвует в формировании окончательного результата (и теряется).

[Х]_доп. = Х_зн Х_n X_n-1…X_i…X₁

+

[Y]_доп. = Y_зн Y_n Y_n-1…Y_i…Y₁

3. Результат суммирования получают в дополнительном коде, если он отрицательный и в прямом коде если положительный.

4. Модули операндов и результат их суммирования должны быть меньше единицы.

2.5.1 Сумматор дополнительных кодов.

На рис.2.5 представлен многоразрядный двоичный сумматор дополнительных кодов.

S_зн S_n S_n-1 S₁

ОДС_n-1

ОДС₁

ОДС_н

ОДС_зн

ОДС₁

Р_зн . . . . . Р₁

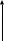Р_n-2

X_зн Y_зн X_n Y_n X_n-1 Y_n-1 X₁ Y₁

Рис.2.5 Многоразрядный двоичный сумматор дополнительных кодов.

ОДС – одноразрядный двоичный сумматор;

S – сумма;

Р – перенос информации из одного ряда в другой;

│X│< 1

│Y│< 1

│S│< 1

X, Y – операнды заданные дополнительными кодами, модули которых должны быть меньше единицы.

Пример 1:

Х = + 0,10011100

Y = - 0,00110101

X+Y= 0,01100111

Проверка:

[X]_доп. = 0 10011100^{перенос}

+

[Y]_доп. = 1 11001011

[X+Y]_доп. = 0 01100111 = [X+Y]_пр.

Пример 2:

X = - 0,01110101 [Х]_доп. = 1 10001011

Y = - 0,01001010 [Y]_доп. = 1 1011011

X+Y = -0,10111111 [X+Y]_доп. = 1 01000001

Пример нарушения условия 4 по результату операции:

X = - 0,10101010 [X]_под. = 101010110

Y = - 0,11000011 [Y]_доп. = 100111101

X+Y = - 1,01101101 [X+Y]_доп. = 010010011

Проверка показывает, что модуль результата > 1.

│X+Y│=│S│>1