Раздел 2.

Аналитическая геометрия

Глава 1. Геометрия на плоскости Системы координат на плоскости

Прямая, на которой указано направление, начало отсчета и масштаб называется числовой осью. Прямоугольная (декартова) система координат на плоскости состоит из двух взаимно перпендикулярных числовых осей, пересекающихся в точке O – начале системы координат. Горизонтальную ось называют осью абсцисс, а вертикальную - осью ординат.

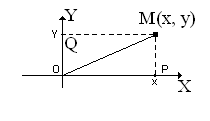
Каждой точке плоскости M сопоставляется ориентированный отрезок OM (радиус-вектор с началом в точке О и концом в точке M. Спроектируем точку М на оси координат (рис.1.1). Каждой точке плоскости M сопоставляется упорядоченная пара чисел (х,y), которые называются декартовыми координатами точки М(х,у). В любой системе координат существует взаимнооднозначное соответствие между точкой и ее координатами. На плоскости расстояние d между двумя точками M(х_i,y_i) и N(x_j,y_j) измеряется по прямой и вычисляется по формуле длины вектора

d² = (x_i - x_j)² + (y_i - y_j)²

или (1.1)

.

Рис. 1.1. Декартова система координат.

Пример. Найти расстояние d между двумя точками M(-3,4) и N((5.2). Согласно формуле (1.1) имеем

.

Полярная система координат. Выберем на плоскости фиксированную точку O, называемую полюсом, и исходящую из нее полуось OP, называемую полярной осью. На полярной оси указываем единицу масштаба. В этой системе координат (рис.1.2) положение точки M задается ее расстоянием r до полюса (т.е. длиной отрезка OM, называемого полярным радиусом точки M) и углом , который составляет полярный радиус с полярной осью (положительный отсчет угла идет против часовой стрелки), причем - <   или 0  <2. Числа r и  называются полярными координатами точки М(r, ).

Если на плоскости заданы прямоугольная и полярная системы координат, причем начало координат и положительная часть оси абсцисс совпадают с полюсом и осью полярной системы координат (рис.1.3), то декартовы и полярные координаты точки М связаны м соотношением

х = r cos y = r sin . (1.2)

Формулы (1.2) выражают координаты точки M в прямоугольной системе через ее же координаты в полярной системе. Отсюда

х² + y² = r²(cos²+ sin² )= r² . (1.3)

tg = . (1.4)

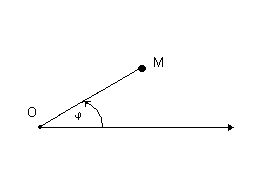
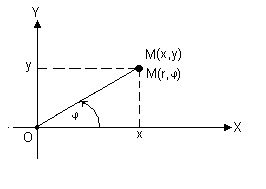
Рис. 1.2. Полярная система координат. Рис. 1.3. Связь полярной и декартовой систем координат.

Преобразование системы координат. Пусть даны две прямоугольные системы координат X₁Y₁ и X₂Y₂ (рис.1.4 а). Найдем связь координат точки M(x₁,y₁) в одной из систем координат с ее же координатами (x₂,y₂) в другой системе. Для этого вначале совместим начала координат, сохраняя старые направления осей (рис.1.4 б), потом одну из систем повернем так, чтобы оси совпали направления координат.

Параллельный перенос системы координат. В первой системе координат точка O₁ имеет координаты (0,0), точка O₂ - (а,b), а точка M - (x₁,y₁). Рассматривая проекции этих точек на оси координат первой системы имеем

х₁ = а + x₂, y₁ = b + y₂. (1.5а)

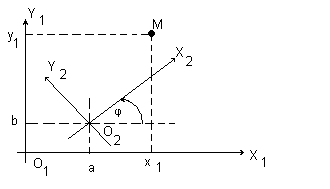
1.4 а. 1.4 б.

Рис. 1.4. Преобразования координат.

Чтобы получить координаты во второй системе, необходимо провести обратные действия. Это приведет к зависимостям

x₂ = x₁ - a. y₂ = y₁- b. (1.5 б)

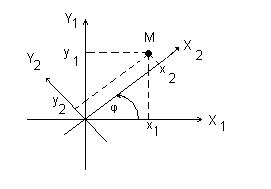
Поворот системы координат с совмещенной точкой начала. Пусть оси OX₁ и OX₂ повернуты на угол . Из рис. 1.4 б следуют соотношения

x₁ = x₂cos - y₂ sin (1.6)

y₁ = x₂ sin - y₂ cos.

В общем случае связь между координатами точки в различных прямоугольных системах координат выражается линейными соотношениями

х₁ = х₂cos - y₂ sin + a

y₁ = x₂ sin + y₂ cos + b (1.7)

или

x₂ = x₁ cos + y₁ sin - a

y₂ = -x₁ sin + y₁ cos - b.

Пример. Как изменятся координаты точки M(-2,3), если система будет повернута на 30⁰ и сдвинута вверх на две единицы?

Применяя формулы (1.7) для x₁= -2, y₂ = 3, угла  = 30⁰, а =0 и b = 2, имеем

x₂ = -2cos30⁰ + 3sin30⁰ = -2 + 3 = -

y₂ = 2sin30⁰ +3cos30⁰ - 2 = 2 + 3 -2 = - 1

Прямая линия на плоскости.

Пусть прямая линия пересекает ось ординат в точке B(0, b) под углом  к оси абсцисс (см. рис.1.5.а). Выберем на прямой произвольную точку M(x,y) (такая точка называется текущей). Проекции направленного отрезка BM на оси координат соответственно равны пр_хBM = х, пр_уBM = y - b. При скольжении точки M по прямой проекции изменяются, однако, их отношение, равное

tg  = = k (1.8)

сохраняется для всех точек прямой и не выполняется для точек не принадлежащих прямой. Тангенс угла φ называется угловым коэффициентом и обозначается k.