4 Тепловой расчет системы

Данная система будет использована для плавки меди, физические параметры приведены в таблице 4.1.

Таб.4.1-Исходные данные.

Плотность меди, г/см3
Масса слитка из меди, кг	m=20
Теплоемкость меди, Дж/кг*к	с=380
Удельная теплота плавления меди, кДж/кг
Температура плавления меди, K	Tпл=1312

4.1 Расчет импульсного режима.

Величина скважности:

Время одного импульса: с

Период следования импульсов: (с)

Частота следования импульсов: (Гц)

По условию сказано, что нужно расплавить 20кг меди. Рассчитаем количество тепла для расплавки материала:

_(4.1)

(МДж)

Где с=380Дж/кг*к – теплоемкость меди, кДж/кг- удельная теплота плавления меди, Tпл – температура плавления меди, m- масса меди.

Так как 1Вт = 1Дж/с, то можно посчитать, сколько выделится тепла за один импульс:

(Дж) (4.2)

где Р – мощность электронного пучка.

Рассчитаем количество импульсов и общее время необходимое для расплавки 20 кг меди:

_(4.3)

(с) (4.4)

_{Найдем массу, которая расплавиться за один импульс:}

=2 (г) (4.5)

(см³) (4.6)

Где г/см³- плотность меди.

На рисунке 4.1 изображена схема плавления меди.

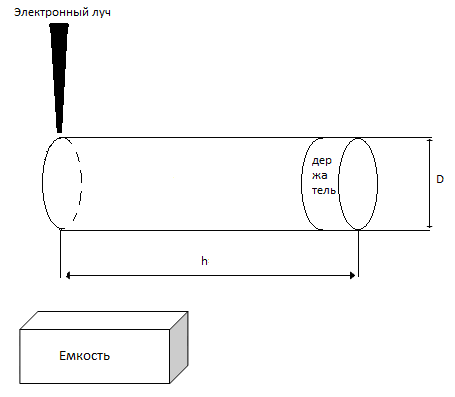
Рис.4.1 – Схема плавления меди.

Допустим, что заготовка меди представляет собой цилиндрический слиток с радиусом см. Объем меди:

см³ (4.7)

и высота слитка

см. (4.8)

Пусть начальная температура заготовки К (или 25°C). Количество тепла, необходимое для того, чтобы расплавить 20 кг меди будет равно:

(МДж) (4.9)

Тепло, излучаемое от заготовки со стороны плавки (P1), центральной части цилиндра (P2) и со стороны держателя (P3):

(Вт)

(Вт) (4.10)

(Вт) где - интегральный коэффициент излучения для меди ;

Вт/см²*К² - постоянная Больцмана;

(см²)

(см²) (4.11)

(см²)

Определим количество тепла теряющегося за счет теплопроводности меди:

, (4.12)

(кДж/кг)- удельная теплота плавления;

(кДж) (4.13)

Держатель возьмем из вольфрама.

- интегральный коэффициент излучения для вольфрама ( )

Тепло, излучаемое от держателя, когда плавим болванку в начале (P₄), в середине (P₅) и со стороны держателя (P₆):

(Вт)

(Вт) (4.14)

(Вт)

Где (см²)- площадь держателя (4.15)

Что бы учесть, тот факт, что слиток будет остывать между импульсами, рассчитаем время между импульсами и тепло, которое теряет слиток за это время:

(с) (4.16)

(с) (4.17)

Тепло, теряемое заготовкой за время охлаждения: со стороны плавки (Q₂), центральной части цилиндра (Q₃) и со стороны держателя (Q₄):

(кДж)

(кДж) (4.18)

(кДж)

Суммарное количество тепла, необходимое на нагрев, плавку, лучеиспускание и охлаждение через металл равно , где . Тогда выражение для расчета необходимого времени выглядит следующим образом:

(4.19)

с

Подставляя полученные значения , , , , , , , из (4.9)–(4.18) соответственно получим, что потребуется секунд для того, чтобы расплавить 20 кг меди если использовать непрерывный режим. Так как у нас режим импульсный надо учесть время между импульсами.

Рассчитаем сколько всего импульсов:

(шт.) (4.20)

Рассчитаем общее время в импульсном режиме:

(с) (4.21)

Сборочный чертеж, а так же 3D модель электронно-оптической установки представлены в приложении А и в приложении В, соответственно.