9.3 Пределы применимости формулы эйлера. Полная диаграмма критических напряжений

Вывод формулы Эйлера (9.4) основан на интегрировании дифференциального уравнения упругой линии стержня. Это уравнение справедливо только в пределах линейной зависимости между напряжениями (5.4) и деформациями (3.5), поэтому и формула Эйлера применима только до тех пор, пока критические напряжения, определяемые по этой формуле, не превосходят предела пропорциональности σ_пц, т. е. при условии

.

Используя соотношение i_min=I_min/F, где i_min – наименьший радиус инерции площади (3.15) поперечного сечения стержня, можем записать это условие так:

.

Введем обозначение гибкости стержня:

.

(9.3)

Безразмерная величина отношения расчетной длины стержня к радиусу инерции площади его поперечного сечения называется гибкостью.

Тогда критические напряжения определятся как

. Откуда нетрудно получить величину предельной гибкости, при которой деформации стержня будут упругими:

.

Например, для конструкционной малоуглеродистой стали с σ_пц=210 МПа и E=2.1·10⁵ МПа формулой Эйлера (9.4) можно пользоваться лишь при гибкости стержня

.

Тщательно поставленные опыты показали справедливость формулы Эйлера для стержней большой гибкости. В то же время эти опыты подтвердили неприменимость формулы Эйлера для стержней, гибкость которых . Для таких стержней формула Эйлера (9.4) дает значения критических нагрузок, превышающие их действительные значения. Попытки использовать формулу Эйлера для стержней средней и малой гибкости приводили иногда к серьезным катастрофам. Теория устойчивости стержней за пределом пропорциональности была развита Карманом, Энгессером, Шенли, Тетмайером, Ясинским...

Наибольшее распространение получила формула определения критических напряжений, предложенная Ф.С. Ясинским (1895 г.):

(9.4)

В этой формуле λ – гибкость стержня, a и b – коэффициенты, зависящие от свойств материала. Например, для стали 3 при σв=380 МПа и σт=240 МПа формула (13.17) имеет вид:

(МПа).

По формуле (9.4) проводится расчет на устойчивость стержней средней гибкости, разрушение которых при сжатии сопровождается значительным боковым выпучиванием. Для стержней малой гибкости (λ<λ₁) понятие потери устойчивости неприменимо в том смысле, в каком применяется для стержней большой гибкости. Стержни, у которых длина невелика по отношению к размерам поперечного сечения, выходят из строя главным образом из-за того, что напряжения сжатия в них достигают предела текучести σ_т (при пластичном материале) или предела прочности σ_вр (при хрупком материале). Поэтому для стержней малой гибкости в качестве критического напряжения принимается предел текучести σ_т или предел прочности σ_вр. Четкой границы между стержнями малой и средней гибкости провести нельзя. В расчетах принимают .

Зависимость критических напряжений σ_кр от гибкости λ изображается графически в виде полной диаграммы критических напряжений. Такая диаграмма для малоуглеродистой стали представлена на рис. 9.6.

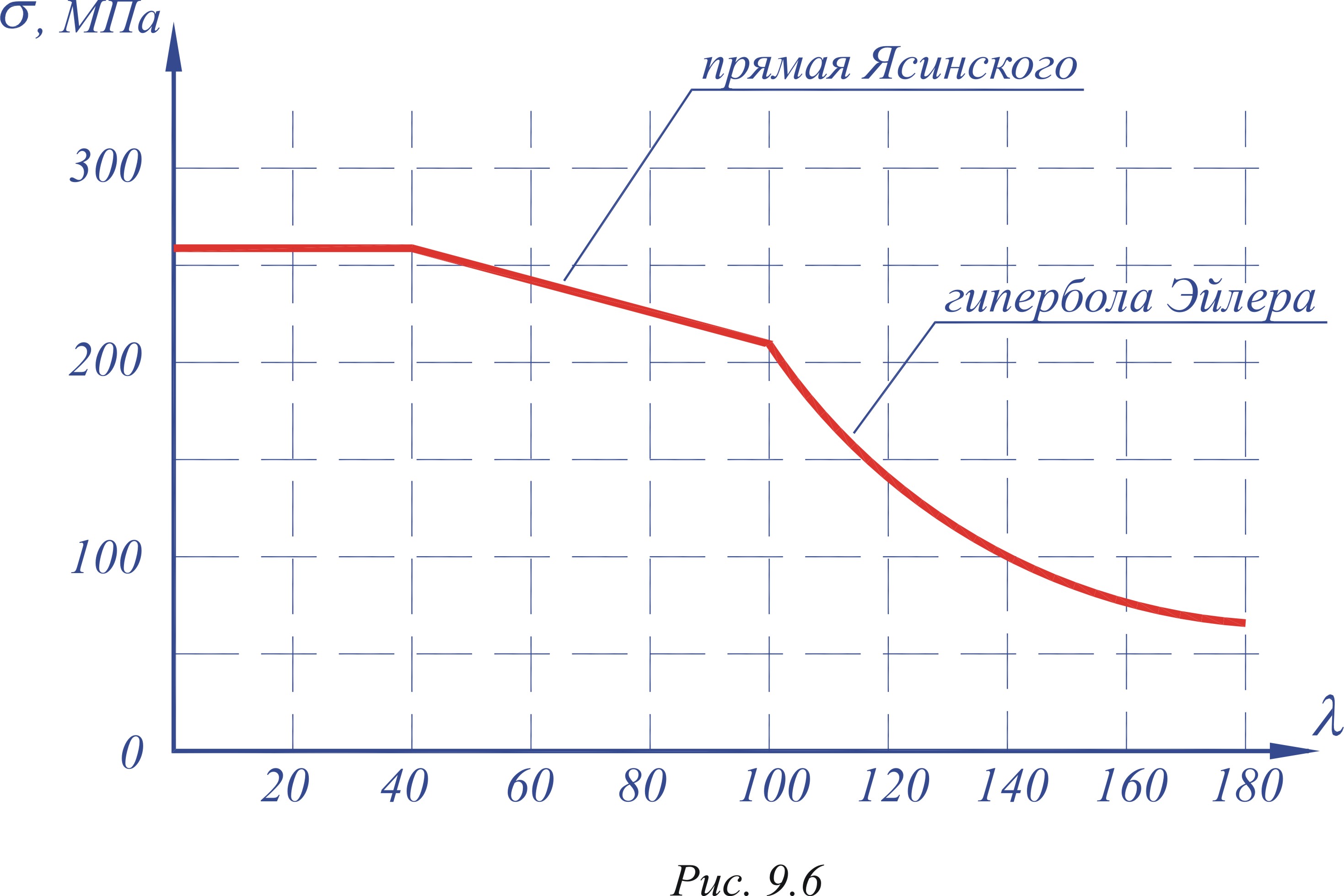
Для стержней малой гибкости ( ) зависимость σ_кр от λ выражена горизонтальной прямой, для стержней средней гибкости ( ) – наклонной прямой в соответствии с зависимостью Ясинского (9.4), а для стержней большой гибкости ( ) – гиперболой Эйлера. Если известна гибкость рассчитываемого стержня, то критическое напряжение может быть найдено непосредственно по диаграмме критических напряжений.