19. Проверка равенства двух коэффициентов детерминации

Важным направлением использования статистики Фишера является проверка гипотезы о равенстве нулю не всех коэффициентов регрессии одновременно, а только некоторой части этих коэффициентов.

Пусть первоначально построенное по n наблюдениям уравнение регрессии имеет вид:

Y=b₀+b₁X₁+b₂X₂+…+b_m-kX_m-k+…+b_mX_m

И коэффициент детерминации для этой модели равен R₁². Исключим из рассмотрения k объясняющих переменных. По первоначальным n наблюдениям для оставшихся факторов построим другое уравнение регрессии:

Y=c₀+c₁X₁+c₂X₂+…+c_m-kX_m-k

Для которого коэф. Детерминации равен R₂². Очевидно, R₂²≤R₁², т.к. каждая дополнительная переменная объясняет часть рассеивания зависимой переменной. Возникает вопрос: существенно ли ухудшилось качество описания поведения зависимой переменной Y? На него можно ответить, проверяя гипотезу H₀: R₁²-R₂²=0 и используя статистику F=[(R₁²-R₂²)/(1-R₁²)][(n-m-1)/k] (1). В случае справедливости H₀ приведенная статистика имеет распределение Фишера с числами степеней свободы v₁=k, v₂=n-m-1. Действительно, соотношение (1) может быть переписано в виде F=[(R₁²-R₂²)/k]/[(1-R₁²)/(n-m-1)]. Здесь (R₁²-R₂²) – потеря качества уравнения в результате отбрасывания k объясняющих переменных; k – число дополнительно появившихся степеней свободы; (1-R₁²)/(n-m-1) – необъясненная дисперсия первоначального уравнения.

По таблицам критических точек распределения Фишера находят Fкр=Fα;m;n-m-1 (α – требуемый уровень значимости). Если рассчитанное значение Fнабл статистики превосходит Fкр, то нулевая гипотеза о равенстве коэффициентов детерминации должна быть отклонена. В этом случае одновременное исключение из рассмотрения k объясняющих переменных некорректно, т.к. существенно превышает R₂². Если же наоборот наблюдаемая F-статистика невелика, то это означает, что разность R₁²-R₂² незначительна. Следовательно, можно сделать вывод, что в этом случае одновременное отбрасывание k объясняющих переменных не привело к существенному ухудшению общего качества уравнения регрессии, и оно вполне допустимо.

Аналогичные рассуждения могут быть использованы и по поводу обоснованности включения новых k объясняющих переменных. В этом случае рассчитывается F-статистика F=[(R₂²-R₁²)/(1-R₂²)][(n-m-1)/k].

Добавлять переменные целесообразно, как правило, по одной. Кроме того, при добавлении объясняющих переменных в уравнение регрессии логично использовать скорректированный коэф. детерминации.

20. Проверка гипотезы о совпадении уравнений регрессии для двух выборок. Распространенным тестом проверки данной гипотезы является тест Чоу, суть которого состоит в следующем.

Пусть имеются две выборки объемами n₁, n₂ соответственно. Для каждой из этих выборок оценено уравнение регрессии вида: Y=b_0k+b_1kX₁+b_2kX₂+…+b_mkX_m+e_k, k=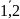 . Проверяется нулевая гипотеза о равенстве друг другу соответствующих коэффициентов регрессии H₀=b_j1=b_j2, j=0,1,…,m.

Другими словами будет ли уравнение регрессии одним и тем же для обеих выборок?

Пусть суммы ∑e_ik² (k=1,2) квадратов отклонений значений y_i от линий регрессии равны S₁, S₂ соответственно для первого и второго уравнений регрессии. Пусть по объединенной выборке объема (n₁+n₂) оценено еще одно уравнение регрессии, для которого сумма квадратов отклонений y_i от уравнения регрессии равнаS₀.

Для проверки H₀ в этом случае строится следующая F-статистика: F=[(S₀-S₁-S₂)/(S₁+S₂)][(n₁+n₂-2m-2)/(m+1)]

В случае справедливости H₀ построенная F-статистика имеет распределение Фишера с числами степеней свободы v₁=m+1; v₂=n₁+n₂-2m-2. Очевидно, F-статистика близка к нулю, если S₀≈S₁+S₂, и это фактически означает, что уравнения регрессии для обеих выборок практически одинаковы. В этом случае F>Fкр=Fα;v1;v2. Если же F>Fкр, то нулевая гипотеза отклоняется.

21. Статистика Дарбина-Уотсона. Для анализа коррелированности случайных отклонений используется статистика Дарбина-Уотсона (DW), которая определяется по следующей формуле: DW=∑(e_i-e_i-1)²/∑ e_i².

Для больших значений n считается, что ∑e_i²≈∑e_i-1². Тогда ∑(e_i-e_i-1)²=∑(e_i²-2e_ie_i-1+e_i-1²)=2(∑e_i²-∑e_ie_i-1).

Тогда DW=2(∑e_i²-∑e_ie_i-1)/∑e_i²=2(1-r_ei,ei-1). Если e_i≈e_i-1, то r_ei,ei-1=1, DW=0; если e_i≈-e_i-1, то r_ei,ei-1=-1. DW=4; 0<DW<4.

Понятно, что при случайном поведении случайных отклонений в одной половине случаев знаки последовательных отклонений совпадают, а в другом противоположны. А абсолютные значения случайных отклонений в среднем одинаковы DW=∑1/2(2e_i)²/∑e_i²=2. Следовательно, необходимым условием независимости случайных отклонений является близость к 2 значения DW. Грубым правилом можно считать отсутствие автокорреляции и остатков, если 1,5<DW<2,5

22. Логарифмические модели.Пусть некот. эконом. зависимость моделируется формулой Y=A*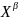 , (7.1) где А и β – параметры модели (т. е. константы, подлежащие определению). Эта функция может отражать зависимость спроса Y на благо от его цены X (в данном случае β < 0) или от дохода Х (в данном случае β > 0; при такой интерпретации переменных Х и Y функция (7.1) назыв. функцией Энгеля). Функция (7.1) может отражать также зависимость объема выпуска Y от использования ресурса Х (производ- ственная функция), в которой 0 < β < 1, а также ряд других зависимостей. Для упрощения выкладок случайное отклонение ε введем в соотношение позднее. Модель (7.1) не является линейной функцией относительно Х. Стандартным и широко исп-м подходом к анализу функцией данного рода в эконометрике является лога-рифмирование по экспоненте (по основанию e = 2.71828…). Такие логарифмы назыв. натур. логарифмами и обозначаются lnY, lnX. Прологарифмировав обе части (7.1), имеем:

lnY= lnA+ вlnX . (7.2) После замены lnA = β 0 , (7.2) примет вид: вlnY =в0+ вlnX . (7.3) С целью статистической оценки коэф-тов добавим в м-ль случайную погрешность ε и получим так называемую двойную логар-ю м-ль (и зависимая переменная и объясняющая переменная заданы в логарифмическом виде): lnY=в0+ вlnX+е. (7.4) Не являясь линейным относительно X и Y, данное ур-е явл. линейным относительно lnX и lnY, а также относительно параметров β 0 и β 1. Вводя замены и Y*= lnY и X*= lnX, (7.4) можно перепис. в виде: Y*=в0+ вX*+е. (7.5)

Модель (7.5) является лин. м-лью. Если все необх. предпосылки классич. ли н. регрессионной модели для (7.5) выполнены, то по МНК можно определить наилучшие линейные несмещенные оценки коэфф-в β 0 и β. Отметим, что коэфф-т β определяет эластичность перемен-ной Y по переменной Х, т. е. процентное изменение Y для данного процентного изменения Х. Действительно, продифференцировав ле-вую и правую части (7.4) по Х, получим:

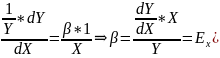) (7.6) Отметим, что в дан. случае коэфф. β является константой, указывая на пост. эластичность. Поэтому зачастую двойная лог. м-ль наз. м-лью пост. эла- стичности.

Заметим, что в случае парной регрессии обоснованность исполь- зования логарифмической модели проверить достаточно просто. Вме- сто наблюдений (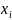 , ) рассм. наблюдения (ln , ln ), i = 1, 2, …, n. Вновь полученные точки наносятся на корреляционное поле. Если их расположение соответствует прямой линии, то произведенная замена удачна и исп. лог. м-ли обосновано. Данная м-ль легко обобщается на большее число переменных. Например,

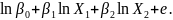
23. Полулогарифмич-е модели. Модели вида lnY=b₀+bX+e (лог-линейная) и Y=b₀+blnX+e (линейно-логарифмич-ая) назыв-ся полулогарифмич-ми мод-ми. Такие модели обычно исп-ют в тех случаях, когда необх-мо опред-ть темп роста или прироста каких-либо эконом-их показателей. Напр-р, или при анализе банк-го вклада по первонач-ому вкладу и %-ой ставке, прироста объема выпуска от относит-го (%-го) увелич-я затрат ресурса, бюджетный дефицит от темпа роста ВНП, темп роста инфляции от объема денежной массы и т.д.

24. Обратная модель. Модель вида 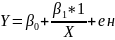азывается обратной моделью. Эта модель сводится к линейной заменой 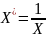. Данная модель обычно применяется в тех случаях, когда неограниченное увеличение объясняющей переменной Х асимптотически приближает зависимую переменную Y к некоторому пределу (в данном случае к . В зависимости от знаков и характерны следующие ситуации:

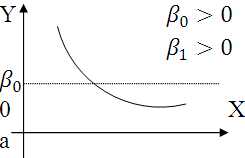
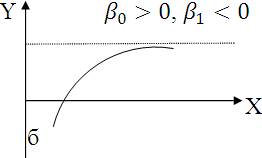
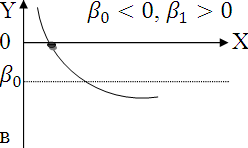
График а может отражать зависимость между объемом выпуска (Х) и средними фиксированными издержками (У). График б может отражать зависимость между доходом Х и спросом на блага У так называемые функции Торнквиста ( в этом случае 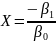- минимально необходимый уровень). Важным приложением графика, изображенного на рис. в является кривая Филлипса, отражающая зависимость между уровнем безработицы (Х) в процентах и процентным изменениям заработной платы (У). При этом точка пересечения кривой с осью 0Х определяет естественный уровень безработицы.

25 Степенная модель. 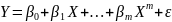Степенная функция вида при m=3 (кубическая функция) в микроэкономике моделирует зависимость общих издержек от объема выпуска; квадратичная функция (m=2) отражает зависимость между объемом выпуска и средними или предельными издержками (или между расходами на рекламу и прибылью). Модель может быть сведена к линейной модели множественной регрессии с помощью замены . X→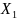 , 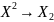…. 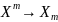Параметры модели ищут с помощью МНК.