10.2 Закон полного внутреннего отражения

Заменив в формуле (10.1) n₁₂ выражением (10.2), закон преломления можно представить в виде

. (10.3)

Из формулы (10.3) видно, что при переходе света из оптически более плотной среды в оптически менее плотную (n₁n₂) преломленный луч света удаляется от нормали к поверхности раздела двух сред, т.е. угол  больше угла . Увеличение угла падения  сопровождается более быстрым ростом угла преломления  и, при достижении углом  значения

, (10.4)

угол  становится равным /2. Угол падения, при котором угол преломления равен /2, называется предельным углом падения. Если угол падения  будет больше предельного угла падения _пред,, то наблюдается явление полного внутреннего отражения: луч света, падающий на границу раздела двух сред полностью отражается обратно в первую среду, а преломление прекращается.

Рисунок 10.2

Рисунок 10.2а

Таким образом, для того, чтобы наблюдалось явление полного внутреннего отражения необходимо осуществление двух условий: 1) луч должен переходить из среды оптически более плотной в среду оптически менее плотную; 2) угол падения должен быть больше значения предельного угла падения.

На измерении предельного угла падения основано устройство рефрактометров – приборов для определения показателя преломления жидкостей. В медицине рефрактометры применяются для определения концентрации веществ в растворе (например, позволяют контролировать качество приготовления лекарственных препаратов).

Рисунок 10.3.

Явление полного внутреннего отражения лежит в основе волоконной оптики. Свет, попадая внутрь прозрачного волокна, окруженного веществом с меньшим показателем преломления, многократно отражается от боковой поверхности волокна и распространяется вдоль этого волокна. Диаметр этих тонких стеклянных или пластиковых волокон может быть доведен до нескольких микрометров. Для передачи больших световых потоков и сохранения гибкости светопроводящей системы отдельные волокна собираются в пучки (жгуты) – световоды. Рисунок 10.3 демонстрирует, как распространяется свет по тонкому волокну, испытывая только скользящие отражения от стенок, т.е. полное внутреннее отражение. Если световоду придать сложную форму, то угол падения обычно превышает предельный, и свет будет передан от одного торца световода до другого практически без ослабления. Этот эффект используется в декоративных светильниках и при подсветке струй в фонтане. Световоды можно использовать для освещения труднодоступных мест, например, внутренних органов человека. Вводя через пищевод больного световод, врач получает возможность визуально обследовать стенки желудка. По одним волокнам посылается свет для освещения желудка, а по другим идет отраженный свет. На противоположном торце световода наблюдатель видит серию светлых и темных пятен (как на телевизионном экране), т.е. картину у противоположного торца световода. Волокна должны быть оптически изолированы друг от друга. Обычно на них наносится вещество с меньшим показателем преломления. Волокна должны быть строго параллельны, иначе изображение не получится четким. Чем больше волокон в световоде и чем они тоньше, тем лучше разрешаются детали изображения.

Рисунок 10.4

10.3 Принцип Ферма

В основу геометрической оптики может быть положен принцип Ферма. Из этого принципа вытекают законы прямолинейного распространения, отражения и преломления света. В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.

Для прохождения прямолинейного участка пути ds (cм. рис.10.4) свету требуется время , где – скорость распространения света в данной среде. Заменив через с/n, получим, что . Следовательно, время , затрачиваемое светом на прохождение пути от точки 1 до точки 2, равно . Имеющая разность длины величина называется оптической длиной пути. В однородной среде оптическая длина пути равна произведению геометрической длины пути s на показатель преломления среды n: . 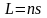Пропорциональность времени прохождения  оптической длине пути L дает возможность сформулировать принцип Ферма следующим образом:

свет распространяется по такому пути, оптическая длина которого минимальна.