3.1 Гармонические колебания

Рисунок 3.1

Самый простой вид собственных колебаний – это гармонические колебания.

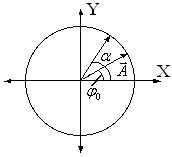
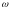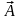Гармонические колебания представляют собой периодический процесс, в котором изменение величины происходит по закону синуса (или косинуса). Пусть движение материальной точки описывается радиус-вектором и пусть точка совершает равномерное движение по кругу с угловой скоростью вращения (см. рисунок 3.1). Тогда проекции радиус-вектора на оси и можно записать следующем образом,

. (3.0)

Таким образом, изменение проекций вектора на оси и происходит по законам синуса и косинуса. Поэтому движение по окружности можно считать гармоническим колебательным движением.

В формулах (3.0) величины и называются смещением. Смещение равно расстоянию колеблющейся точки от положения равновесия в произвольный момент времени.

Наибольшее смещение колеблющейся точки от положения равновесия называется амплитудой колебаний, в выражении (3.0) – это величина .

За один оборот колеблющаяся точка вернется в свое первоначальное положение, а проекция ее радиус-вектора совершит одно полное колебание.

Периодом колебаний (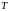 ) называется время, в течение, которого материальная точка совершит одно полное колебание.

Частотой колебаний ( ) называется число полных колебаний, совершенных в единицу времени, поэтому период и частота колебаний связаны следующим соотношением:

,

где – называют круговой (или циклической) частотой гармонических колебаний.

Циклическая частота колебаний связана с периодом колебаний и частотой

.

Частоту измеряют в герцах, размерность [Гц]=1/сек.

Переменная является аргументом синуса и косинуса и называется фазой колебания; параметр 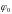называется начальной фазой. Начальная фаза показывает положение колеблющейся точки в начальный момент времени.

3.2 Скорость и ускорение гармонического колебания

Рисунок 3.2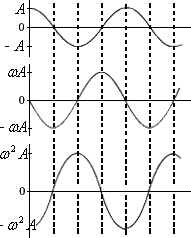

Пусть смещение колеблющейся точки определяется законом

(3.1)

Тогда согласно законам механики скорость движения этой точки определяется первой производной смещения по времени:

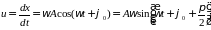, (3.2)

т.е. скорость изменяется по гармоническому закону, опережая смещение по фазе на 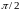. При прохождении положения равновесия скорость материальной точки достигает максимального значения .

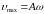Ускорение же определяется первой производной скорости по времени

(3.3)

и также как и скорость изменяется по гармоническому закону, опережая смещение по фазе на .

Графики смещения, скорости и ускорения гармонического осциллятора изображены на рисунке 3.2. Обратите внимание на то, что скорость отличается по фазе от смещения на , а ускорение – на .

3.3 Колебания пружины

Рисунок 3.3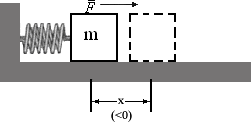

Простейшим примером гармонического колебания, служат колебания груза на конце пружины. Многие другие виды колебательных движений проявляют большое сходство с этими колебаниями; например, колебания, происходящие в системе кровообращения, дыхания, сокращения мышц. Поэтому мы разберем этот пример подробно. Будем считать, что массой пружины можно пренебречь и, что пружина установлена горизонтально, как показано на рисунке 3.3.

К одному концу пружины прикреплен груз массой m, который движется без трения по горизонтальной поверхности. Любая пружина имеет определенное значение длины, при котором с ее стороны на груз не действует сила; в этом случае говорят, что пружина находится в положении равновесия. Если сдвинуть груз вправо, растягивая пружину, или влево, сжимая ее, то пружина действует на груз с силой, которая стремится вернуть его в положение равновесия; такую силу называют возвращающей. Для нашей системы возвращающая сила прямо пропорциональна расстоянию , на которое сжимается или растягивается пружина (см. рисунок 3.3):

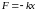. (3.4)

Знак минус означает, что возвращающая сила всегда противоположна по направлению перемещению . Если на рисунке 3.3 мы направим ось, например, вправо, заметим, что положение равновесия мы выбрали в точке 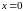. Когда пружину сжимают, сила направлена вправо (см. рисунок 3.3), а перемещение влево. Постоянная величина в формуле (3.4), называется жесткостью пружины.

Что же произойдет, если пружину растянуть на длину , и затем отпустить? Пружина действует на груз с силой, которая стремится вернуть его в положение равновесия. Но поскольку эта сила сообщает грузу ускорение, груз приходит в положение равновесия со значительной скоростью. Заметим, что в положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна (см. рисунок 3.2). Когда груз, проскочив положение равновесия, движется влево, сила со стороны пружины замедляет его, и в точке 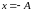груз на мгновение останавливается, а затем начинает двигаться в противоположном направлении, пока не придет в точку , откуда он начал движение. Затем весь этот процесс повторяется. Рассматриваемый колебательный процесс происходит лишь под действием внутренней силы – силы упругости, поэтому рассматриваемые колебания являются собственными.

Уравнение второго закона Ньютона для груза на пружине имеет вид:

.

Преобразуем это уравнение следующим образом:

. (3.5)

Коэффициент при положителен, поэтому его можно представить в следующем виде:

. (3.6)

Применяя в уравнении (3.5) обозначения (3.6), получим:

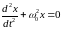. (3.7)

Таким образом, движение груза под действием силы вида (3.4) описывается линейным, однородным дифференциальным уравнением второго порядка.

Легко убедиться, что общее решение уравнения (3.7) имеет вид:

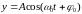. (3.8)

Смещение изменяется со временем по закону косинуса. Следовательно, движение системы, находящейся под действием силы , представляет собой гармоническое колебание. Из уравнения (3.8) следует, что введенный коэффициент представляет собой частоту колебаний и называется собственной частотой колебаний системы, находится по формуле

. (3.9)

Из формулы (3.9), очевидно, что частота собственных колебаний системы определяется свойствами самой системы, т.е. ее упругими свойствами.