8.3.2 Анализ колебаний нелинейной системы. Метод Гольдфарба

Условие возникновения автоколебаний в нелинейной системе имеет вид:

Это условие можно записать в виде .

Амплитуду и частоту автоколебаний можно определить из условии

Решить систему нелинейных уравнений относительно и не всегда удаётся. Гольдфарб предложил графический метод определения условий возникновения автоколебаний и амплитуды и частоты автоколебаний.

Условия возникновения автоколебаний представлены в виде:

,

где - инверсный комплексный коэффициент усиления нелинейного звена.

Для определения условий возникновения колебаний амплитуды и частоты построим годографы комплексного коэффициента передачи линейной части и инверсного .

Если годографы пересекаются, в системе возможны автоколебания (1 и 2). Для определения точки устойчивых автоколебаний положим, что область, лежащая слева эквивалентна наличию корней с отрицательной вещественной частью, а справа – положительной вещественной частью.

Рассмотрим точку 1. Пусть по каким-то причинам амплитуда уменьшилась, мы попадаем в область эквивалентную наличию корней с отрицательной вещественной частью и амплитуда со временем будет затухать до нуля. Пусть по каким-то причинам в точке амплитуда увеличилась, мы попадаем в область эквивалентную наличию корней с положительной вещественной частью, и амплитуда будет увеличиваться до точки 2. Из этого следует, что в точке 1 неустойчивые автоколебания.

Рассмотрим точку 2. Пусть по каким-то причинам амплитуда колебаний увеличилась, и попадаем в область эквивалентную наличию корней с отрицательной вещественной частью. Из этого следует, что амплитуда уменьшилась до точки 2. Пусть по каким-то причинам амплитуда уменьшилась, и мы попадаем в область эквивалентную наличию корней с отрицательной вещественной частью, амплитуда будет возрастать до точки 2. Из этого следует, что в точке 2 устойчивые автоколебания.

По известной реальной и мнимой части точки по таблица годографа определим амплитуду , а по таблица годографа определим частоту автоколебаний.

Пример №1. Исследуем автоколебания в линейной системе АСН, которые могут возникать из-за люфта редуктора.

Если - годографы не пересекаются, автоколебания отсутствуют. С увеличением возрастает амплитуда колебаний и уменьшается их частота.

8.4 Анализ линейных систем при случайных воздействиях

Используется следующие методы:

1. метод, основанный на теории Марковских случайных процессов и сводящихся к решению линейных дифференциальных уравнений 1-2-ого порядка. Уравнения Фоккера-Планка;

2. метод статистической линеаризации;

3. метод моделирования на ЭВМ.

8.4.1 Метод статистической линеаризации

Сущность метода состоит в замене нелинейного элемента статистически эквивалентным ему линейным.

Используются два критерия статистической эквивалентности:

1. равенство математических ожиданий и дисперсий на выходе НЭ и ЛЭК;

2. требуют минимум среднего квадрата отклонений процессов на выходах НЭ и ЛЭК

Представим в виде математического ожидания и центрированной составляющей:

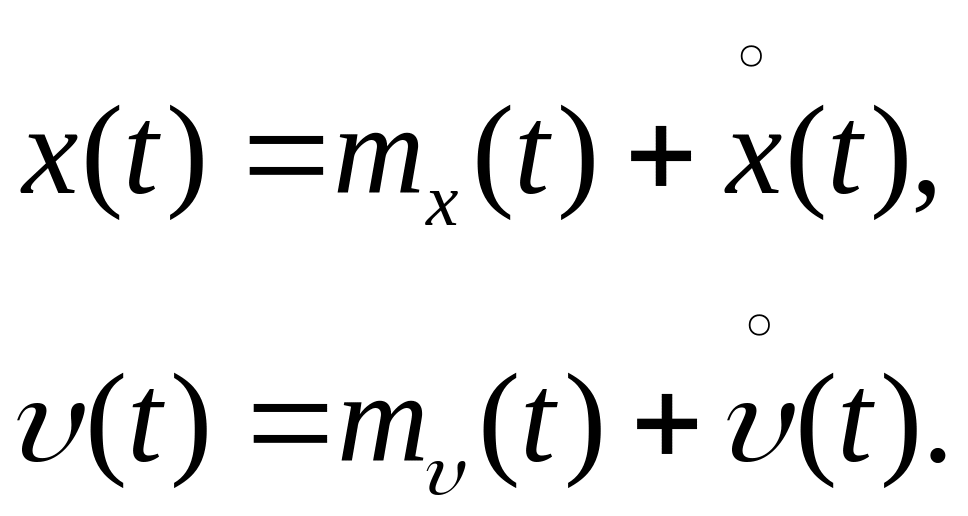
Аппроксимируем выходной сигнал ЛЭК ,

где - коэффициенты статистической линеаризации.

Рассмотри первый критерий:

, отсюда .

, отсюда

Рассмотрим второй критерий:

,

,

,

,

.

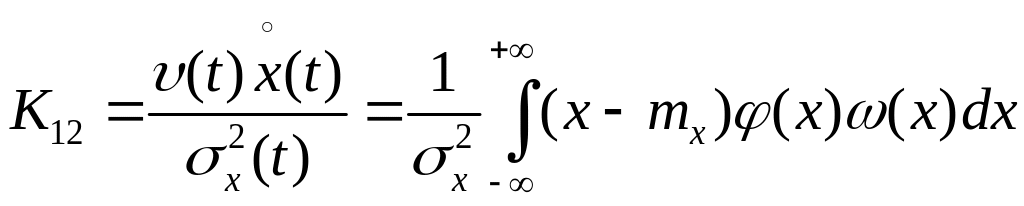Коэффициенты статистической линеаризации зависят не только от характера нелинейности, но и от законов распределений входного процесса. Часто полагают, что входной процесс описывается нормальным гауссовским законом распределением. В этом случае .

Метод является приближенным, потому что не учитывает изменения законов распределения и законов функции на выходе нелинейного элемента.

Пример №1. Найдём коэффициенты для дискриминатора с синусоидальной характеристикой и нормального закона распределения входного процесса.

,

,

.
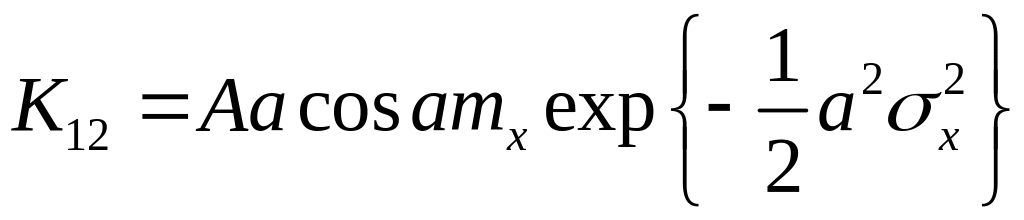