1.3 Обзор главной темы

LDPC коды являются одними из наиболее важных кодов, определённых на графах. Всё это из-за их выдающейся производительности и гибкой структуры. Как уже упоминалось выше, многие коды, определённые на графах были подвержены влиянию структурой LDPC кодов. Это делает исследование LDPC кодов центральным в этой области.

LDPC коды уже используются в таких стандартах, как ETSI EN 302 307 для цифрового видео вещания [26] и IEEE 802.16 (Вещательное Рабочее Сообщество Беспроводного доступа) для кодирования ортогональных систем частотно мультиплексного доступа (OFDMA систем) [27].

В области LDPC кодирования всё ещё остаётся много открытых вопросов. Данная работа ответит на многие вопросы, но в свою очередь откроет целый ряд новых.

1.3.1 Главная тема данной работы

В данной работе описываются эффективные методы разработки и анализа низкоплотных кодов с проверкой на чётность (LDPC кодов) и их декодирования. Эти проблемы изучаются с практической точки зрения, а также будет поднят ряд новых интересных вопросов. Некоторые из этих вопросов получат ответ в данной работе, а некоторые останутся в качестве открытых. Короче говоря, в этой работе рассматриваются три основные проблемы:

• эффективные методы для анализа LDPC кодов;

• эффективные методы проектирования нерегулярных LDPC кодов; • улучшенные стратегии для декодирования LDPC кодов.

Хотя основной упор делается на LDPC коды, некоторые из этих проблем обсуждаются за пределами их применения к LDPC кодам. В этом разделе мы рассмотрим общую структуру данной работы, а также представим краткое описание главных результатов.

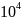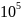На рис. 1.2 сравниваются типичные представления нерегулярных LDPC кодов длиной и с турбо кодами равной длины на AWGN канале. Турбо коды могут превзойти LDPC коды на коротких длинах блоков, но как можно увидеть из рис. 1.2, если длина блока является большой (как правило, более 5000), нерегулярные LDPC коды превосходят турбо коды равной длины. С увеличением длины кодов улучшается производительность. 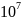LDPC коды длиной могут быть надежно расшифрованы с помощью отношения Eb/N0 с точностью, менее чем на 0,1 дБ отличающейся от предела Шеннона на AWGN канале, а при длине блока отклонение до предела Шеннона может составлять менее 0,04 дБ [28].

Эта удивительная производительность достигается за счет тщательной разработки нерегулярности кода. К сожалению, за исключением нескольких случаев, эти методики расчета могут быть очень насыщены вычислениями. Традиционный метод проектирования заключается в создание некоторой нерегулярности в коде, проверяющей работу с плотностью эволюции, и изменении неравномерности в коде до желаемой производительности. Одна интересная проблема, которая рассматривается в литературе, заключается в упрощении методики расчета LDPC кодов [24]. Это будет одним из основных направлений этой работы.

Рисунок 1.2: Сравнение производительности между уровнем ½ LDPC кодов различной длины с турбо кодами одинаковой длины.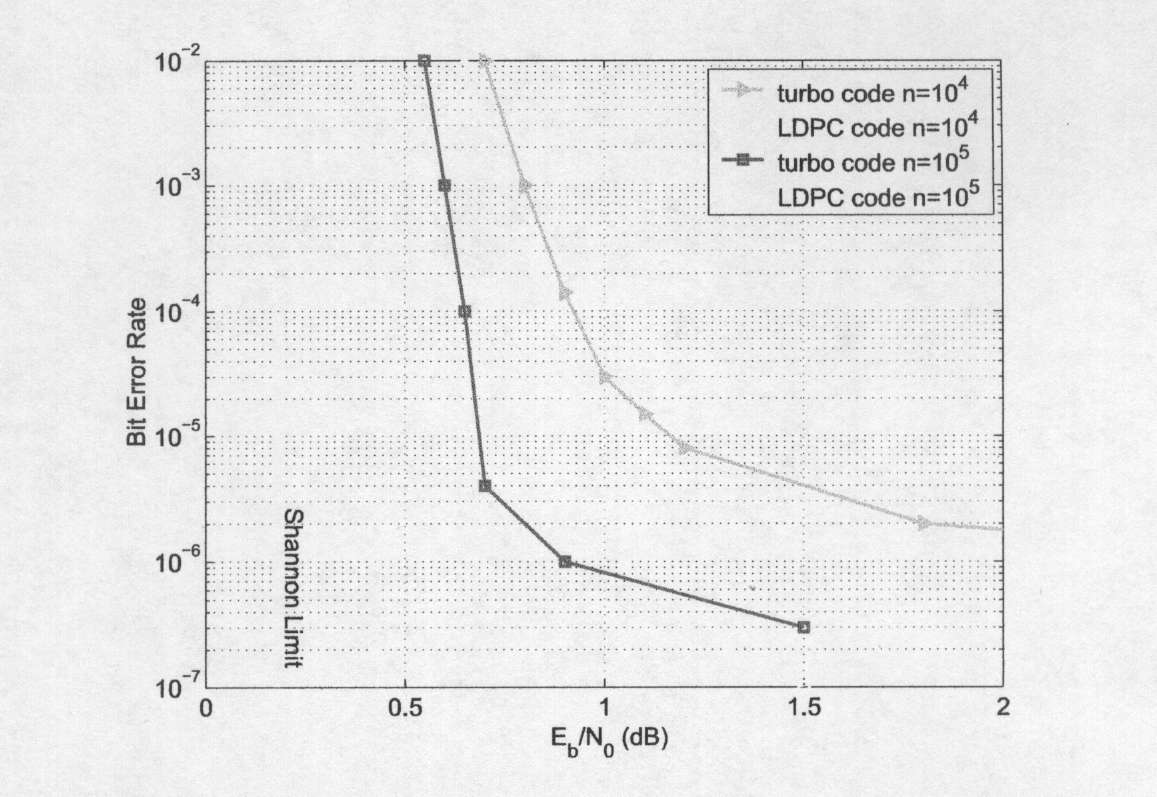

В результате получается двоичный линейный код длины n и размерности к> = п - г, с равенством тогда и только тогда, когда все проверочные ограничения линейно независимы. Проверочной матрицей H этого кода является матрица смежности графа G, т. е. (Ij) входящие в H, hij, равно 1, тогда и только тогда, когда Ci (i-ый узел проверки) подключен к Vj (j-ому переменному узлу).

LDPC коды могут быть расширены до GF(д), рассматривая множество ненулевых весов ш, J 6 GF (д) для рёбер В. Проверочная матрица в этом случае формируется с помощью множества весов. Другими словами HIJ - Wij. В оставшейся части данной работы мы предполагаем, что коды – двоичные, если не указано иное.

Это легко объясняется, если предположить, что любой двудольный граф Q приводит к линейному коду. В случае LDPC кодов число E ребер в фактор графе, сравнимое с количеством ребер в построенном случайно двудольном графе, то есть двудольном графе, который с вероятностью 1/2 имеет грань между левой вершиной V и правой вершиной с, очень мало. Как мы увидим позже, для LDPC кода с фиксированной скоростью R, число ребер порядка n, а случайно построен двудольном графе - R) края. Таким образом, с ростом п, количество уменьшается, что приводит к редкому коду.

LDPC коды, в зависимости от их структуры, могут быть классифицированы, как регулярные или нерегулярные. Регулярные коды имеют переменные узлы с фиксированными степенями и проверочные узлы с фиксированными степенями. Обозначая степень переменных узлов, как d_v и степень проверочных узлов, как d_c получим:

E — r ■ d_c = n ■ d_v.

Таким образом, скорость кода R может быть вычислена, как

Д:=*>И^Г ₌ (2.3)

n n d_c

Если строки H линейно независимы, то R - 1 - JFC. В ряде работ величина ^ называется проектируемой скоростью [12], но обычно возможная линейная зависимость между строками H игнорируется и проектируемая скорость считается равной действительной.

Теперь рассмотрим ансамбль регулярных LDPC кодов с переменной степенью d_v, проверочной степенью d_c и длиной п. Если п достаточно велико, среднее поведение этого ансамбля почти во всех случаях концентрируется вокруг ожидаемого поведения [12]. Следовательно, регулярные LDPC коды относятся к своим переменным и проверочным степеням и их длинам. Когда производительность и свойства бесконечно долгие (или достаточно долгие) на регулярные LDPC коды следует обратить внимание, они будут представлены только степенью их переменного и проверочного узла. Например, (3, 6) LDPC код ссылается на код с переменным узлом степени 3 и проверочным узлом степени 6. Проектируемая скорость этого кода из (2.3) 1/2.

Хотя показатели регулярных LDPC кодов близки к пропускной способности, они показывают больший интервал от пропускной способности, чем турбо коды. Основное преимущество регулярных LDPC коды над турбо кодами заключается в их лучшей, так называемой, "ошибке нижнего уровня". Из Рис. 1.2 следует, что, по сравнению с низким в SNR, для умеренных и высоких компании SNR, BER кривой турбо-коды имеют меньший наклон. Это явление называется ошибкой пола. Рис. 3 в [36] показывает качественное поведение BER против Eb/N0 для турбо кодов и классифицирует различные регионы кривой BER. Явление ошибка пола является фундаментальным свойством из-за низкой свободного расстояния турбо-коды [3]. Таким образом, турбо кодов будет испытывать ошибки пола даже при оптимальном декодировании. LDPC коды однако, как заметил в [9] и его можно увидеть на рис. 1,2 лучше ошибка пола. Кроме того, в работе [37], что LDPC кодов может достичь предела Шеннона при оптимальном декодировании.

LDPC коды стали более привлекательными, когда Luby соавт. показали, что разрыв в мощности могут быть сокращены с помощью нерегулярно коды LDPC [17].LDPC код называется нерегулярной, если, по его коэффициент графика, не все переменные (и / или проверить) узлы имеют равные степени. Тщательно проектирования неравномерность графика, коды, которые выполняют очень близко к мощности можно найти [13,17,21,28]. Ансамбль нерегулярные коды LDPC определяется его переменным распределением степени края Л = {Л2, Аз, ...} и его проверка края степень распределения V - {р2, Рз-• • •}, где обозначает долю ребра на переменную узлов степени г и р обозначает долю ребра на проверку узлов степени у. Другой способ описания той же ансамбль кодов, представляя последовательности и V с их порождающих многочленов Л (ж) = Yh и р (х) - YliPix% 1 - Оба обозначения, введенные в [17] и были использованы влитературы впоследствии. Обратите внимание, что график характеризуется с точки зрения доли краям каждой ступени, а не в узлах каждой степени. Позже мы увидим, что это представление является более удобным. В оставшейся части этого тезиса, по переменным (чек) степень распределения,

мы имеем в виду переменную (чек) края степень распространения. Как и регулярные коды, показано в [12], что среднее поведение почти во всех случаях ансамбля неправильный код сосредоточен вокруг ожидаемого поведения, когда код достаточно велик. Кроме того, ожидаемое поведение сходится к циклу без дела [12]. Учитывая степень распределения LDPC код и число ребер е, легко видеть, что число переменных узлов п

_{n = E}J2~ = E f X(x)dx, (2.4)

. г J о

и число контрольных узлов г

r = E= E fp(x)dx. (2.5)

< ¹

Поэтому дизайн скорости код будет

Я = 1-ЦлГ (2-6)

или, что эквивалентно

fn p(x)dx

Д = 1 — ° . (2.7)

/о 4x)dx

Найти хорошего асимптотически долго семьи нерегулярно коды эквивалентно нахождению хорошее распределение степени. Очевидно, что для различных приложений, различные атрибуты являются предпочтительными. Задача нахождения степени распределения в результате чего семейный кодекс с некоторыми нужными свойствами не является тривиальной задачей и будет одним из направлений этого тезиса. Мы пытаемся сформулировать исполнении семейного кодекса с точки зрения степени его распределения в легкой форме, чтобы обеспечить максимальную гибкость в стадии проектирования, и в то же время мы избегаем слишком упрощение, чтобы наши предсказал результаты, близкие к реальным результатам .