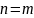Задача № 6 з теорії ймовірностей

Побудувати критерій перевірки гіпотези про рівність дисперсій при відомих математичних сподіваннях для нормального розподілу.

При побудові критеріїв для перевірки статистичних гіпотез діють наступним чином:

Обирається деяка статистика , яка являється мірою розбіжності статистичного і теоретичного законів розподілу і називається статистикою критеріїв або критерієм. Далі знаходять розподіл в припущенні, що розподіл спостережень співпадає з гіпотетичним.

Визначають таке , щоб , де - число (рівень значущості). Якщо міра обчислена по спостереженням , тоді відхилення від теоретичного розподілу вважається значущим і гіпотеза відхиляється. Якщо ж , то дані експерименту не суперечать гіпотезі.

Необхідно перевірити гіпотезу проти альтернативної гіпотези 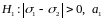і - відомі. Для цього існує критерій Фішера.

Незміщене значення вибіркової дисперсії:

Відомо, що та має розподіл відповідно з і ступенями свободи. Тоді при справедливості гіпотези відношення цих величин не залежить від значення дисперсії, і має розподіл Фішера з , ступенями свободи.

Задача № 7 з теорії ймовірностей

Нехай – незалежні події. Довести, що

.

і – незалежні події, якщо .

Застосуємо метод математичної індукції.

1. 

– очевидно, що виконується.

2. 

3. доведемо, що якщо виконується для , то виконується і для

Нехай

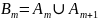
Задача № 8 з теорії ймовірностей

Нехай – незалежні події з . Довести, що ймовірність того, що жодна з цих подій не відбудеться, визначається формулою

.

З того, що – незалежні події та за властивістю спадковості слідує, що також незалежні події. Ймовірність, що подія не настала . Ймовірність перетину незалежних подій дорівнює добутку їх імовірностей. Тому

Задача № 9 з теорії ймовірностей

Нехай – випадкова величина. Довести, що

.

Дана нерівність називається нерівністю Чебишева.

Доведення

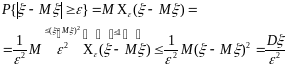
Задача № 10 з теорії ймовірностей

Побудувати критерій перевірки гіпотези про рівність математичних сподівань при невідомих рівних дисперсіях для нормального розподілу.

Маємо дві незалежні вибірки з розподілу та -

Необхідно перевірити гіпотезу проти альтернативної гіпотези = - але невідомі.

Випадкові величини мають нормальний розподіл і відповідно. Тоді має нормальний розподіл . Якщо вірна гіпотеза , то має стандартний нормальний розподіл .

.

З Леми Фішера 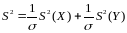має -розподіл з ступенями свободи і не залежить від . Величина має розподіл Стьюдента . Якщо підставити всі значення, легко переконатися, що 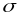скорочується. Отримаємо . Якщо С – відподіний до рівня значущості квантиль розподілу Стьюдента, то ми приймаємо , якщо