
Теорія Ймовірності практика
Зміст
Задача № 1 з теорії ймовірностей
Дати
означення дискретного ланцюга Маркова,
істотних та неістотних станів та
зробити класифікацію станів ланцюга
з матрицею перехідних ймовірностей
|
4 |
Задача № 2 з теорії ймовірностей
Дати означення дискретного ланцюга Маркова, істотних та неістотних станів та зробити класифікаціюстанів ланцюга з матрицею перехідних ймовірностей :
|
5 |
Задача № 3 з теорії ймовірностей
Дати
означення характеристичної функції
та довести, що сума двох незалежних
випадкових величин, що мають розподіл
Пуассона з параметрами
|
6 |
Задача № 4 з теорії ймовірностей
Дати
означення ефективної оцінки та
перевірити на ефективність оцінку
|
7 |
Задача № 5 з теорії ймовірностей
Побудувати критерій перевірки гіпотези про рівність математичних сподівань при відомих дисперсіях для нормального розподілу.
|
8 |
Задача № 6 з теорії ймовірностей
Побудувати критерій перевірки гіпотези про рівність дисперсій при відомих математичних сподіваннях для нормального розподілу.
|
9 |
Задача № 7 з теорії ймовірностей
Нехай
|
10 |
Задача № 8 з теорії ймовірностей
Нехай
– незалежні події з
|
11 |
Задача № 9 з теорії ймовірностей
Нехай
|
12 |
Задача № 10 з теорії ймовірностей
Побудувати критерій перевірки гіпотези про рівність математичних сподівань при невідомих рівних дисперсіях для нормального розподілу.
|
13 |
Задача № 1 з теорії ймовірностей
Дати означення дискретного ланцюга Маркова, істотних та неістотних станів та зробити класифікацію станів ланцюга з матрицею перехідних ймовірностей :
.
Озн:
X1,
X2,…,
Xn,…
послідовність
випадкових величин, кожна з яких приймає
значення з множини Xn={0,1,2,…},
називається ланцюгом Маркова, якщо має
місце властивість: для будь-яких
n1<n2<…<nk

 за
n
кроків.
за
n
кроків.
 -
матриця перехідних ймовірностей.
Перехідна ймовірність ланцюга Маркова
за один крок:
-
матриця перехідних ймовірностей.
Перехідна ймовірність ланцюга Маркова
за один крок:
 .
.
 -
матриця.
-
матриця.
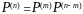

Стан
і назив. неістотним, якщо існують такі
числа m
(число кроків) та стан j,
що ми можемо перейти зі стану i
в j
за m
кроків
 >0,
але для всіх n>=1
>0,
але для всіх n>=1
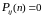 .
.
Нехай
d(i)
найбільший спільний дільник тих n
, для яких
 .
Якщо d(i)>1,
то і періодичний, d(i)=1,
то і неперіодичний.
.
Якщо d(i)>1,
то і періодичний, d(i)=1,
то і неперіодичний.
Розв'язок.
Класифікацію проводимо за таким планом:
Чи є матриця стохастичною (Матриця стохастична , коли сума чиел в кожному рядку = 1)
Які стани є суттєвими а які ні. (Стан А суттєвий, коли: для будь якого стану В, якщо В досяжний з А то А досяжний із В. А досяжний із В якщо ймовірність потрапити з А до В за n кроків більше нуля хочаб для одного натурального n.)
Які стани є періодичними а які ні. (Стан є періодичним якщо НСД( Pn ,n >0)) >1 , де Pn – ймовірність повернутися в наш стан рівно за n кроків)
Чи є ЛМ звідним чи ні (суттєві стани ЛМ за відношенням „досяжності" розбивається на класси еквівалентності. Якщо таких классів лише один – то ЛМ –незвідний.)

Матриця стохастична
Суттєві : 5,3. Несуттєві – 1,2,4 (бо можна потрапити в 3 а назад не можна)
3,4,5 – неперіодичні бо P1>0 і тому НСД =1. 1,2 –періодичні з періодом 2.
Звідний. Один класс – (3) і другий (5)

 :
:
 .
. .
.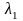 ,
,
 відповідно, має пуассонівський розподіл
з параметром
відповідно, має пуассонівський розподіл
з параметром
 .
. параметра
параметра
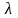 розподілу Пуассона.
розподілу Пуассона. .
.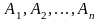 – незалежні події. Довести, що
– незалежні події. Довести, що .
. .
Довести, що ймовірність
.
Довести, що ймовірність
 того, що жодна з цих подій не відбудеться,
визначається формулою
того, що жодна з цих подій не відбудеться,
визначається формулою .
.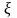 – випадкова величина. Довести, що
– випадкова величина. Довести, що

 .
.