Тема 5. Корреляционный метод

131. Задание {{ 116 }} ТЗ-1-111.

 r_xy = 0,982  r_xy = – 0 ,991  r_xy = 0,871

132. Задание {{ 117 }} ТЗ-1-112.

 r_xy = 0,982  r_xy = – 0 ,991  r_xy = 0,871

133. Задание {{ 118 }} ТЗ-1-113.

 r_xy = 0,982  r_xy = – 0 ,991  r_xy = 0,871

134. Задание {{ 119 }} ТЗ-1-114.

Межгрупповая дисперсия составляет 61% от общей дисперсии.

Эмпирическое корреляционное отношение = ... (с точностью до 0,01).

Правильные варианты ответа: 0,78; 0.78; РЕШЕНИЕ: = 61% = 0,61; = 0,7810 = 0,78

135. Задание {{ 120 }} ТЗ-1-115.

Для измерения тесноты корреляционной связи между двумя количественными признаками используются ... .

 коэффициент корреляции знаков  коэффициент эластичности

 линейный коэффициент корреляции  коэффициент корреляции рангов

136. Задание {{ 121 }} ТЗ-1-116.

Эмпирическое корреляционное отношение представляет собой корень квадратный из отношения ... дисперсии(й).

• средней из групповых дисперсий к общей

•  межгрупповой дисперсии к общей

 межгрупповой дисперсии к средней из групповых

 средней из групповых дисперсий к межгрупповой

137. Задание {{ 122 }} ТЗ-1-117.

Теснота связи двух признаков при нелинейной зависимости определяется по формуле

  

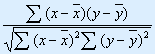
138. Задание {{ 123 }} ТЗ-1-118.

Корреляционный анализ используется для изучения ... .

 взаимосвязи явлений  развития явления во времени  структуры явлений

139. Задание {{ 124 }} ТЗ-1-119.

Тесноту связи между двумя альтернативными качественными признаками можно измерить с помощью коэффициентов ... .

 знаков Фехнера  корреляции рангов Спирмена

 ассоциации  контингенции  конкордации

140. Задание {{ 125 }} ТЗ-1-120.

Парный коэффициент корреляции показывает тесноту ... .

 линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель

 линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель

 связи между результативным признаком и остальными, включенными в модель

 нелинейной зависимости между двумя признаками

141. Задание {{ 126 }} ТЗ-1-121.

Частный коэффициент корреляции показывает тесноту ... .

 линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель

 линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель

 нелинейной зависимости

 связи между результативным признаком и остальными, включенными в модель

142. Задание {{ 127 }} ТЗ-1-122.

Парный коэффициент корреляции может принимать значения ... .

 от 0 до 1  от -1 до 9  от -1 до 1

 любые положительные  любые меньше нуля

143. Задание {{ 128 }} ТЗ-1-123.

Частный коэффициент корреляции может принимать значения ... .

 от 0 до 1  от -1 до 9  от -1 до 1

 любые положительные  любые меньше нуля

144. Задание {{ 129 }} ТЗ-1-124.

Множественный коэффициент корреляции может принимать значения ... .

 от 0 до 1  от -1 до 9  от -1 до 1

 любые положительные  любые меньше нуля

145. Задание {{ 130 }} ТЗ-1-125.

Коэффициент детерминации может принимать значения ... .

 от 0 до 1  от -1 до 9  от -1 до 1

 любые положительные  любые меньше нуля

146. Задание {{ 131 }} ТЗ-1-126.

В результате проведения регрессионного анализа получают функцию, описывающую ... показателей

 взаимосвязь  соотношение  структуру  темпы роста  темпы прироста

147. Задание {{ 132 }} ТЗ-1-127.

Если результативный и факторный признаки являются количественными, то для анализа тесноты связи между ними могут применяться...

 корреляционное отношение  линейный коэффициент корреляции

 коэффициент ассоциации  коэффициент корреляции рангов Спирмена

 коэффициент корреляции знаков Фехнера

148. Задание {{ 133 }} ТЗ-1-128.

Прямолинейная связь между факторами исследуется с помощью уравнения регрессии

   

149. Задание {{ 134 }} ТЗ-1-129.

Для аналитического выражения нелинейной связи между факторами используются формулы ... .

  

150. Задание {{ 135 }} ТЗ-1-130.

Параметр а₁ (а₁ = 0,016) линейного уравнения показывает, что

 с увеличением признака "х" на 1 признак "у" увеличивается на 0,694

 с увеличением признака "х" на 1 признак "у" увеличивается на 0,016

 связь между признаками "х" и "у" прямая

 связь между признаками "х" и "у" обратная

151. Задание {{ 136 }} ТЗ-1-131.

Параметр а₁ (а₁ = – 1,04) линейного уравнения показывает, что

 с увеличением признака "х" на 1 признак "у" уменьшается на 1,04

 связь между признаками "х" и "у" прямая

 связь между признаками "х" и "у" обратная

 с увеличением признака "х" на 1 признак "у" уменьшается на 36,5

152. Задание {{ 337 }} ТЗ № 337

 2  3  4  3,5

РЕШЕНИЕ: 2

153. Задание {{ 338 }} ТЗ № 338

Коэффициент детерминации представляет собой долю ...

 дисперсии теоретических значений в общей дисперсии

 межгрупповой дисперсии в общей  межгрупповой дисперсии в остаточной

 дисперсии теоретических значений в остаточной дисперсии