Тема 4. Ряды динамики

108. Задание {{ 100 }} ТЗ-1-95.

Cреднегодовой темп роста исчисляется по формулам ... .

   

109. Задание {{ 101 }} ТЗ-1-96.

По формуле определяется …

 базисный темп роста  цепной темп роста

 базисный темп прироста  цепной темп прироста

 абсолютное значение 1% прироста

110. Задание {{ 102 }} ТЗ-1-97.

По формуле определяется …

 базисный темп роста  цепной темп роста

 базисный темп прироста  цепной темп прироста  абсолютное значение 1% прироста

111. Задание {{ 103 }} ТЗ-1-98.

Ежеквартальные темпы прироста должны быть в среднем = ... % (с точностью до 0,1 %), чтобы выручка от реализации продукции в четвертом квартале текущего года по сравнению с четвертым кварталом предыдущего года возросла с 600 тыс. руб. до 798,6 тыс. руб.

Правильные варианты ответа: 7,4; 7.4;

РЕШЕНИЕ: = = 107,4% (+7,4%)

112. Задание {{ 104 }} ТЗ-1-99.

Средний уровень моментного ряда динамики с равными временными промежутками исчисляется по формуле

средней ...

 арифметической простой  арифметической взвешенной

 гармонической простой  гармонической взвешенной

 хронологической простой  хронологической взвешенной

113. Задание {{ 105 }} ТЗ-1-100.

Средний уровень моментного ряда динамики с неравными временными промежутками исчисляется по формуле средней ...

 арифметической простой  арифметической взвешенной

 гармонической простой  гармонической взвешенной

 хронологической простой  хронологической взвешенной

114. Задание {{ 106 }} ТЗ-1-101.

Средний уровень интервального ряда динамики с равными временными промежутками исчисляется по формуле средней ...

 арифметической простой  арифметической взвешенной

 гармонической простой  гармонической взвешенной

 хронологической простой  хронологической взвешенной

115. Задание {{ 107 }} ТЗ-1-102.

Средний уровень интервального ряда динамики с неравными временными промежутками исчисляется по формуле средней ...

 арифметической простой  арифметической взвешенной

 гармонической простой  хронологической взвешенной

 гармонической взвешенной  хронологической простой

116. Задание {{ 108 }} ТЗ-1-103.

Методы, используемые для выявления основной тенденции развития явления во времени:

 расчет средней гармонической  расчет показателей вариации

• аналитическое выравнивание ряда динамики

 метод укрупнения интервалов в ряду динамики

 метод скользящей средней уровней ряда динамики

117. Задание {{ 110 }} ТЗ-1-105.

Правильные варианты ответа: 1154;

РЕШЕНИЕ: продлим t на 2 года, на 2003 г. t = +3, на 2004 г. t = +4, следовательно, = 917,2 + 59,2*4 = 1154

118. Задание {{ 111 }} ТЗ-1-106.

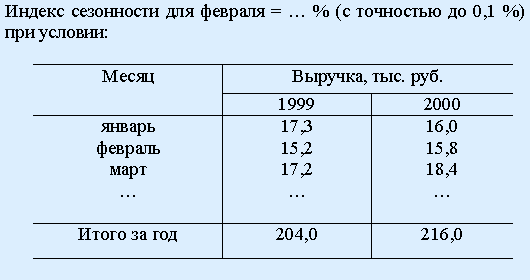
Правильные варианты ответа: 88,6; 88.6;

РЕШЕНИЕ: =(15,2+15,8)/2 = 15,5; =(204,0+216,0)/24 = 17,5; = 15,5/17,5*100 = 88,6

119. Задание {{ 112 }} ТЗ-1-107.

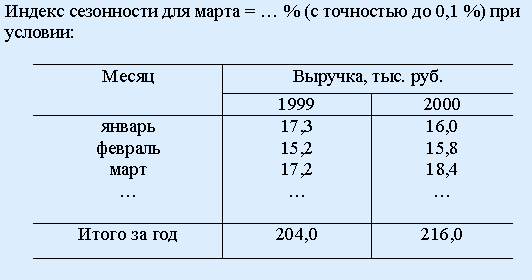
Правильные варианты ответа: 101,7; 101.7;

РЕШЕНИЕ: =(17,2+18,4)/2 = 17,8; =(204,0+216,0)/24 = 17,5; = 17,8/17,5*100 = 101,7

120. Задание {{ 331 }} ТЗ № 331

Ряд динамики характеризует:

 структуру совокупности по какому-либо признаку

 изменение значений признака во времени

 определенное значение варьирующего признака в совокупности

 факторы изменения показателя на определенную дату или за определенный период

121. Задание {{ 332 }} ТЗ № 332

Моментным рядом динамики является:

 остаток оборотных средств предприятия по состоянию на 1 число каждого месяца

 производительность труда на предприятии за каждый месяц года

 сумма банковских вкладов населения на конец каждого года

 средняя заработная плата рабочих и служащих по месяцам года

122. Задание {{ 333 }} ТЗ № 333

Средний уровень моментного ряда динамики при неравных интервалах между датами исчисляется как средняя ...

 арифметическая простая  геометрическая

 хронологическая простая  арифметическая взвешенная

 хронологическая взвешенная

123. Задание {{ 334 }} ТЗ № 334

Разность уровней ряда динамики называется ...

 абсолютным приростом  темпом роста  темпом прироста  коэффициентом роста

124. Задание {{ 335 }} ТЗ № 335

Отношение уровней ряда динамики называется ...

 абсолютным приростом  средним уровнем

 коэффициентом роста  абсолютным значением одного процента прироста

125. Задание {{ 336 }} ТЗ № 336

Базисный абсолютный прирост равен:

 произведению цепных абсолютных приростов

 сумме цепных абсолютных приростов

 корню n-1степени из произведения цепных абсолютных приростов

 корню n-1степени из суммы абсолютных приростов

126. Задание {{ 372 }} ТЗ № 372

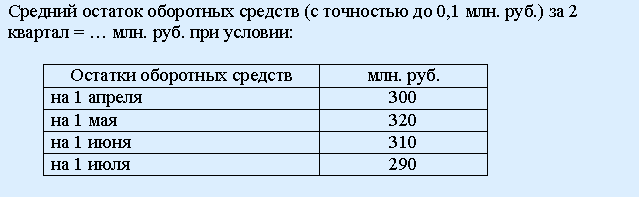
 305,0  310,0  308,3  312,5

РЕШЕНИЕ: моментный ряд, равные интервалы между датами, следовательно, считаем по хронологической простой. (300/2 + 320 + 310 + 290/2)/3 = 308,33333 = 308,3

127. Задание {{ 373 }} ТЗ № 373

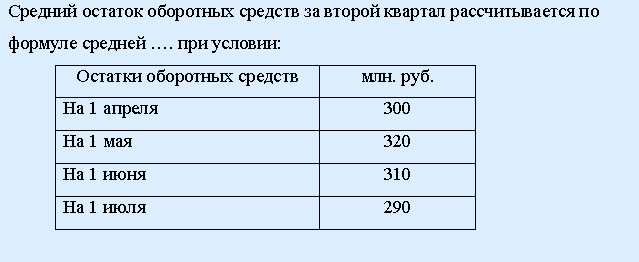
 арифметической  гармонической  геометрической  хронологической  квадратической

РЕШЕНИЕ: моментный ряд, следовательно, считаем по хронологической

128. Задание {{ 384 }} ТЗ № 384

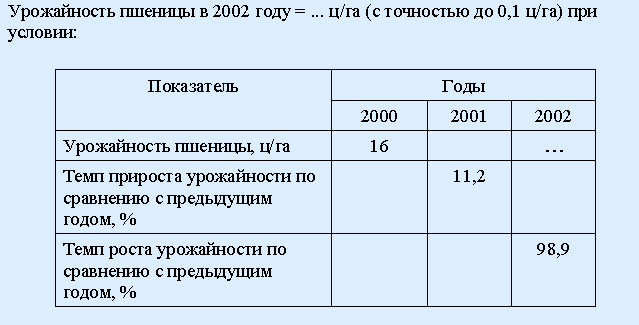
Правильные варианты ответа: 17,6; 17.6;

РЕШЕНИЕ: У₂₀₀₁= У₂₀₀₀*Кр_2001/0= 16 * 1,112; У₂₀₀₂= У₂₀₀₁*Кр_2002/1= 16*1,112 * 0,989 = 17,596 = 17,6

129. Задание {{ 385 }} ТЗ № 385

Правильные варианты ответа: 19,8; 19.8;

РЕШЕНИЕ: У₂₀₀₂= У₂₀₀₀*Кр_2002/0= 17,8 * 1,112 = 19,79 = 19,8

130. Задание {{ 386 }} ТЗ № 386

Правильные варианты ответа: 16;

РЕШЕНИЕ: У₂₀₀₁= У₂₀₀₀*Кр_2001/0; У₂₀₀₂= У₂₀₀₁*Кр_2002/1= У₂₀₀₀*1,112 * 0,989 = 17,6; У₂₀₀₀= 17,6/1,112/0,989=16,00= 16