Тема 3. Индексы
68. Задание {{ 66 }} ТЗ-1-62.
Индекс количества (физического объема) произведенной продукции = ... % (с точностью до 0,1 %) при увеличении объема производства продукции (в стоимостном выражении) на 1,3% и индексе цен, равном 105%.
Правильные варианты ответа: 96,5; 96.5; РЕШЕНИЕ: Iq = Ipq : Ip, 1,013 : 1,05 = 0,96476 = 0,965 = 96,5%
69. Задание {{ 67 }} ТЗ-1-63.
Формулы для расчета индекса фиксированного (постоянного) состава:
70. Задание {{ 71 }} ТЗ-1-67.
Соответствие формул индексов:
индекс цен переменного состава |
|
индекс физического объема продукции |
|
индекс стоимости продукции |
|
индекс цен Пааше |
|
71. Задание {{ 72 }} ТЗ-1-68.
Формула среднего гармонического индекса цен:
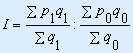
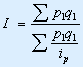
72. Задание {{ 73 }} ТЗ-1-68.
Формула индекса цен переменного состава:
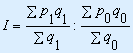
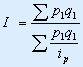
73. Задание {{ 74 }} ТЗ-1-69.
Индекс постоянного состава = ... % (с точностью до 1%), если
индекс переменного состава = 107,8%
индекс структурных сдвигов = 110%.
Правильные варианты ответа: 98; РЕШЕНИЕ: Iпост = Iперем : Iстр, 1,078 : 1,10 = 0,98=98%
74. Задание {{ 75 }} ТЗ-1-70.
Индекс структурных сдвигов = ... % (с точностью до 0,1%), если
индекс постоянного состава = 101,05%,
индекс переменного состава = 100,58%.
Правильные варианты ответа: 99,5; 99.5; РЕШЕНИЕ:
75. Задание {{ 76 }} ТЗ-1-71.
Индекс переменного состава = ... % (с точностью до 0,1%), если
индекс постоянного состава = 102,5%,
индекс структурных сдвигов = 100,6%.
Правильные варианты ответа: 103,1; 103.1; РЕШЕНИЕ:
76. Задание {{ 77 }} ТЗ-1-72.
p0q0 p1q1 q1 p1
77. Задание {{ 78 }} ТЗ-1-73.
Iq = Ipq x Ip Ip = Iq x Ipq Ipq = Iq x Ip Ipq = Iq : Ip
78. Задание {{ 82 }} ТЗ-1-77.
Агрегатный индекс цен при исчислении по одним и тем же данным будет ... среднему(го) гармоническому(го) индексу(а) цен.
меньше меньше или равен больше больше или равен равен
79. Задание {{ 83 }} ТЗ-1-78.
Агрегатный индекс физического объема при исчислении по одним и тем же данным будет ... среднему(го) арифметическому(го) индексу(а) физического объема.
меньше меньше или равен больше больше или равен равен
80. Задание {{ 84 }} ТЗ-1-79.
Агрегатные индексы цен Пааше строятся ...
с весами текущего периода с весами базисного периода без использования весов
81. Задание {{ 85 }} ТЗ-1-80.
Агрегатные индексы физического объема товарооборота строятся ...
с весами текущего периода с весами базисного периода без использования весов
82. Задание {{ 86 }} ТЗ-1-81.
Средний гармонический индекс цен исчисляется с использованием индивидуальных индексов ...
товарооборота и объемов товарооборота отчетного периода
цен и объемов товарооборота отчетного периода
цен и объемов товарооборота базисного периода
физического объема товарооборота и объемов товарооборота базисного периода
83. Задание {{ 87 }} ТЗ-1-82.
Средние индексы исчисляются как средняя величина из индексов ...
индивидуальных цепных агрегатных базисных агрегатных
84. Задание {{ 88 }} ТЗ-1-83.
Произведение промежуточных по периодам цепных индексов дает базисный индекс последнего периода, если это индексы ... .
стоимости индивидуальные
цен с постоянными весами физического объема с переменными весами
физического объема с постоянными весами цен с переменными весами
85. Задание {{ 89 }} ТЗ-1-84.
Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода, если это индексы...
стоимости индивидуальные цен с постоянными весами
физического объема с переменными весами
физического объема с постоянными весами цен с переменными весами
86. Задание {{ 90 }} ТЗ-1-85.
При построении агрегатных индексов качественных показателей используют веса ... периода
отчетного базисного
87. Задание {{ 91 }} ТЗ-1-86.
При построении агрегатных индексов количественных показателей, используют веса ... периода.
отчетного базисного
88. Задание {{ 92 }} ТЗ-1-87.
Iq = Izq x Iz Iz = Iq x Izq Izq = Iq x Iz Izq = Iq : Iz
89. Задание {{ 93 }} ТЗ-1-88.
Iпер.сост. = Iпост.сост. x Iстр.сд. Iпер.сост. = Iпост.сост. : Iстр.сд.
Iпост.сост. = Iпер.сост. x Iстр.сд. Iстр.сд. = Iпост.сост. x Iпер.сост.
90. Задание {{ 94 }} ТЗ-1-89.
Индекс изменения себестоимости газовых плит в ноябре по сравнению с сентябрем = ... % (с точностью до 0,1%) если известно, что в октябре она была меньше, чем в сентябре на 2 %, а в ноябре меньше, чем в октябре на 3,3%
Правильные варианты ответа: 94,8; 94.8;
РЕШЕНИЕ: Iнояб/сент = Iнояб/окт x Iокт/сент = (1-0,033) х (1-0,02) = 0,94766 = 94,8%
91. Задание {{ 95 }} ТЗ-1-90.
Индекс средней выработки продукции в расчете на одного рабочего = ... % (с точностью до 0,1%), если объем выпускаемой продукции увеличился на 15%, а численность рабочих сократилась на 2%.
Правильные варианты ответа: 117,3; 117.3;
РЕШЕНИЕ: ВырабРаб-ка = Выпуск / ЧислРаб-в, следовательно, 1,15 / 0,98 = 1,17347 = 117,3%
92. Задание {{ 96 }} ТЗ-1-91.
Численность рабочих увеличилась на ... % (с точностью до 0,1%), если средняя выработка продукции в расчете на одного рабочего возросла на 12%, а объем выпуска продукции увеличился с 50 тыс. шт. до 60 тыс. шт.
Правильные варианты ответа: 7,1; 7.1;
РЕШЕНИЕ: ЧислРаб-в = Выпуск / ВырабРаб-ка, следовательно, (60/50) / 1,12 = 1,07143 = 107,1% (+7,1%)
93. Задание {{ 97 }} ТЗ-1-92.
Индекс себестоимости единицы продукции = ... % (с точностью до 0,1%), если физический объем продукции снизился на 20%, а производственные затраты увеличились на 6%.
Правильные варианты ответа: 132,5; 132.5;
РЕШЕНИЕ: Iz = Izq : Iq, 1,06 : 0,8 = 1,325 = 132,5%
94. Задание {{ 98 }} ТЗ-1-93.
Индекс производственных затрат = ... % (с точностью до 0,1%), если себестоимость единицы продукции снизилась на 10%, а физический объем продукции возрос на 15%.
Правильные варианты ответа: 103,5; 103.5;
РЕШЕНИЕ: Izq = Iq х Iz, 0,9*1,15 = 1,035 = 103,5%
95. Задание {{ 317 }} ТЗ-1-65.
Формула для вычисления индекса переменного состава:
96. Задание {{ 318 }} ТЗ-1-66.
Формула для вычисления индекса структурных сдвигов:
97. Задание {{ 377 }} ТЗ № 377
уменьшилось на 4% увеличилось на 30% уменьшилось на 30%
увеличилось на 4% не изменилось
98. Задание {{ 378 }} ТЗ № 378
увеличилась на 53% уменьшилась на 53%
уменьшилась на 50% увеличилась на 50% не изменилась
99. Задание {{ 379 }} ТЗ № 379
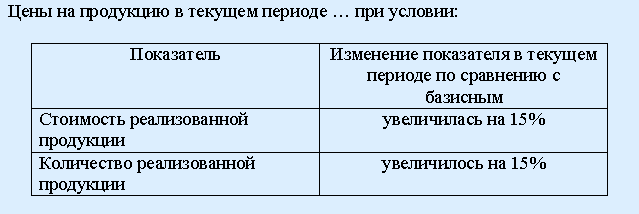
увеличились на 30% увеличились на 4%
уменьшились на 30% уменьшились на 4% не изменились
100. Задание {{ 380 }} ТЗ № 380
Правильные варианты ответа: 9,2; 9.2;
РЕШЕНИЕ: Iиюн/апр = Iиюн/май x Iмай/апр = 1,04*1,05 = 1,092 = 109,2% (+9,2%)
101. Задание {{ 381 }} ТЗ № 381
Произведение сводных (общих) цепных индексов равно базисному индексу только при ... весах.
переменных любых специально подобранных
неизменных (постоянных)
102. Задание {{ 382 }} ТЗ № 382
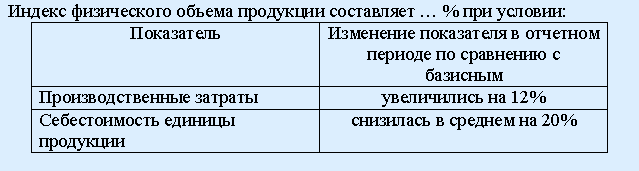
140 92 132 90
РЕШЕНИЕ: Iq = Izq : Iz = 1,12 : 0,8 = 1,4 = 140%
103. Задание {{ 383 }} ТЗ № 383
Изменение средней себестоимости однородной продукции по совокупности предприятий оценивается с помощью индекса ...
переменного состава среднего гармонического
среднего арифметического агрегатного
104. Задание {{ 490 }} ТЗ № 490
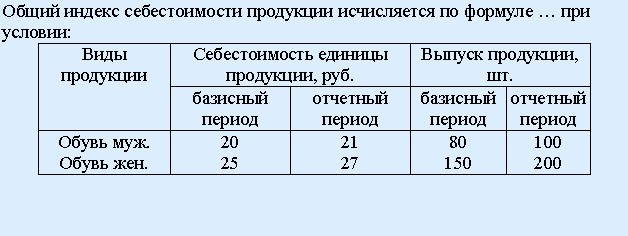
105. Задание {{ 491 }} ТЗ № 491
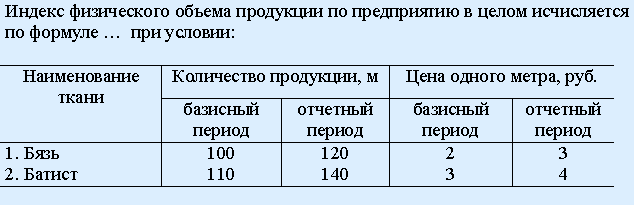
106. Задание {{ 492 }} ТЗ № 492
m = 1000; n = 800 m = 800; n = 1000 m = 32; n = 30 m = 30; n = 32
107. Задание {{ 493 }} ТЗ № 493
m = 200; n = 16 m = 800; n = 15 m = 200; n = 17 m = 300; n = 17