37. Задание {{ 39 }} тз-1-35.
Медиана в ряду распределения = ...:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Правильные варианты ответа: 4; четыре;
РЕШЕНИЕ: данные сгруппированы, следовательно, медиану ищем по накопленным частотам
Накопл. частоты: 8, 24, 41 – больше половины суммы всех частот
38. Задание {{ 40 }} ТЗ-1-36.
Абсолютные показатели вариации:
размах вариации коэффициент корреляции коэффициент осциляции
среднее линейное отклонение среднее квадратическое отклонение
дисперсия коэффициент вариации.
39. Задание {{ 41 }} ТЗ-1-37.
Правильные варианты ответа: 4; хорошо; хорошо;
РЕШЕНИЕ: данные сгруппированы, следовательно, медиану ищем по накопленным частотам
Накопл. частоты: 9, 21, 45 – больше половины суммы всех частот
40. Задание {{ 42 }} ТЗ-1-38.
Правило сложения дисперсий выражено формулой:
41. Задание {{ 43 }} ТЗ-1-39.
Размах вариации:
R
= Xmax
–
R
=
– Xmin
R
= Xmax
– Xmin
R
= X
– Xmin
42. Задание {{ 44 }} ТЗ-1-40.
Правильные варианты ответа: 106;
РЕШЕНИЕ: данные сгруппированы, следовательно, считаем по взвешенной средней арифметической
(108*500+102*300+110*10)/(500+300+10) = 105,8 = 106
43. Задание {{ 45 }} ТЗ-1-41.
Формулы для расчета дисперсии:
44. Задание {{ 46 }} ТЗ-1-42.
Если модальное значение признака больше средней величины признака, то это свидетельствует о ... .
правосторонней асимметрии в данном ряду распределения
левосторонней асимметрии в данном ряду распределения
нормальном законе распределения
биномиальном законе распределения
симметричности распределения
45. Задание {{ 47 }} ТЗ-1-43.
Относятся к относительным показателям вариации:
размах вариации дисперсия
коэффициент вариации среднее линейное отклонение
относительное линейное отклонение
46. Задание {{ 49 }} ТЗ-1-45.
47. Задание {{ 50 }} ТЗ-1-46.
Значение моды определяется на основе графика ...
кривой Лоренца полигона распределения
функции распределения кумуляты огивы
48. Задание {{ 53 }} ТЗ-1-49
Правильные варианты ответа: 4,2; 4.2;
РЕШЕНИЕ: данные сгруппированы, следовательно, считаем по взвешенной средней арифметической
(3*4*75+5*6*70)/(4*75+6*70) = 4,166666 = 4,2
49. Задание {{ 54 }} ТЗ-1-50.
В условиях задачи 48 рассчитайте средний размер товарооборота в расчете на одно предприятие (с точностью до 1 млн.руб)
Правильные варианты ответа: 72; семьдесят два;
РЕШЕНИЕ: данные сгруппированы, следовательно, считаем по взвешенной средней арифметической
(75*4+70*6)/(4+6) = 72
50. Задание {{ 55 }} ТЗ-1-51.
Правильные варианты ответа: 6200;
РЕШЕНИЕ: данные сгруппированы, следовательно, мода соответствует наибольшей частоте
51. Задание {{ 56 }} ТЗ-1-52.
Правильные варианты ответа: 6200;
РЕШЕНИЕ: данные сгруппированы, следовательно, ищем медиану по накопленным частотам
Накопленные частоты: 30, 75, 155 – больше половины суммы всех частот
52. Задание {{ 57 }} ТЗ-1-53.
Дисперсия альтернативного признака ... .
0,5 <
1
0
0
0,25
0,25
1
может принимать любое значение
53. Задание {{ 58 }} ТЗ-1-54.
Мода = ... для значений признака: 3, 3, 3, 5, 5, 6, 9, 11, 12, 13
3 5 6 9 11 12 13
54. Задание {{ 59 }} ТЗ-1-55.
Мода = ... для значений признака: 3, 3, 4, 4, 6, 6, 6, 7, 9, 9
3 4 6 7 9
55. Задание {{ 61 }} ТЗ-1-57.
Дисперсия = ... (с точностью до 0,0001), если при осмотре партии деталей среди них оказалось 2 % бракованных.
Правильные варианты ответа: 0,0196; 0.0196;
РЕШЕНИЕ: дисперсия альтернативного признака = доля*(1-доля) = 0,02*0,98 = 0,0196
56. Задание {{ 62 }} ТЗ-1-58.
Дисперсия = ... (с точностью до 0,0001), если при осмотре 200 деталей среди них оказалось 10 бракованных изделий.
Правильные варианты ответа: 0,0475; 0.0475;
РЕШЕНИЕ: дисперсия альтернативного признака = доля*(1-доля) = (10/200)*(1 – 10/200) = 0,05*0,95 = 0,0475
57. Задание {{ 316 }} ТЗ-1-25.
Формула для расчета дисперсии альтернативного признака:
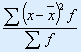
58. Задание {{ 330 }} ТЗ № 330
Расчет среднегодового темпа роста уровня среднедушевого денежного дохода проводится в форме средней ... , если известно, что в 2004 г. по сравнению с 2000 г. он увеличился на 14,5%.
гармонической простой гармонической взвешенной
геометрической арифметической простой арифметической взвешенной
59. Задание {{ 364 }} ТЗ № 364
Медиана в ряду распределения рабочих по уровню заработной платы равна 12 тыс. руб., следовательно ...
среднее значение заработной платы в данном ряду распределения равно 12 тыс. руб.
наиболее часто встречающееся значение заработной платы в данном ряду распределения равно 12 тыс. руб.
наименее часто встречающееся значение заработной платы в данном ряду распределения равно 12 тыс. руб.
50% рабочих имеют заработную плату 12 тыс. руб. и выше
50% рабочих имеют заработную плату не более 12 тыс. руб.
60. Задание {{ 367 }} ТЗ № 367
Правильные варианты ответа: 25;
РЕШЕНИЕ:
=(25*20/100)2=
25
61. Задание {{ 368 }} ТЗ № 368
Правильные варианты ответа: 32,7; 32.7;
РЕШЕНИЕ: =(26*22/100)2= 32,72= 32,7
62. Задание {{ 369 }} ТЗ № 369
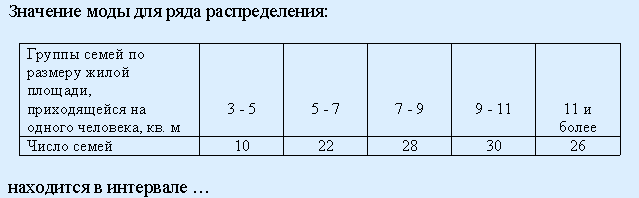
от 3 до 5 от 5 до 7 от 9 до 11 11 и более от 7 до 9
63. Задание {{ 370 }} ТЗ № 370
от 5 до 7 от 3 до 5 от 7 до 9 от 9 до 11 11 и более
РЕШЕНИЕ: данные сгруппированы, следовательно, ищем медиану по накопленным частотам
Накопленные частоты: 10, 32, 60 – больше половины суммы всех частот
64. Задание {{ 371 }} ТЗ № 371
Правильные варианты ответа: 27,3; 27.3;
РЕШЕНИЕ:
V
= (6/22)*100 = 27,2727 = 27,3
65. Задание {{ 374 }} ТЗ № 374
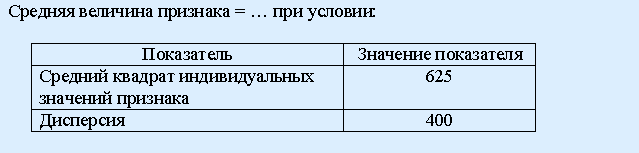
Правильные варианты ответа: 15;
РЕШЕНИЕ:
66. Задание {{ 375 }} ТЗ № 375
арифметической простой арифметической взвешенной
гармонической простой гармонической взвешенной геомерической
РЕШЕНИЕ: Данные сгруппированы, частоты известны, следовательно, по арифметической взвешенной
х – стаж одного рабочего; f – число рабочих
67. Задание {{ 376 }} ТЗ № 376
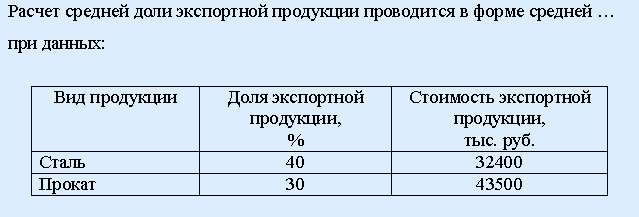
арифметической простой арифметической взвешенной
гармонической простой гармонической взвешенной хронологической
РЕШЕНИЕ: Данные сгруппированы, но частоты неизвестны, следовательно, по гармонической взвешенной
х – доля экспортной продукции; f – стоимость всей продукции = СтЭксп/ДоляЭксп