14. Методика вивчення рівнянь в основній школі. Методика вивчення

Змістова лінія РНС присутня у навчальному матеріалі з 1-го по 12й клас. У поч.шк лише закладаються основи понять рівність,

р-ння, що значить розв р-ння. Розв’язати рівняння означає знайти всі його корені або довести, що їх не існує. Забезпечення здобуття знань і вмінь щодо розв’язування РНС відбувається в основ в основ шк. Тут можна виділити 2 етапи вивчення:

1) 5-6кл(підготовчий)

2) 7-9(основний).

Поняття р-ння з’являється на поч.5-го кл. Зазвичай його тлумачать як рів-ть, що містить невідоме(змінну). Тут же ввод поняття корінь р-ння, що означає роз-ти р-ння. До введ від’ємних чисел методи розв-ня залишаються тими самими що й у поч.шк. за рахунок використання вл-й арифм.дій після введе від’ємних чисел на конкретних.прикладах ввод поняття рівносильності, це розширює види р-нь та методи їх розв-ня. Близько половини навч.часу займає лінія РНС у 7-9кл. У 7-му кл. вводиться поняття лінійного р-ння, розвязуються сис-ми лін. р-нь з 2ма змінними різними методами(графічний, підстановки, додавання).

У 8 кл вивчаються цілі та дробово-рац. р-ння, квадр. р-ння та їх види, р-ння, які зводяться до квадратних, р-ння 2го степеня, сис-ми р-нь 2го степеня. Також як додаткова інформація ввод р-ння з модулями та параметрами. Дана змістова лінія тісно пов’язана з іншими: з числовою (р-ння є мотивацією розширення відомих числових множин), з функціональною (у розв-ні р-нь та їх систем можуть використ. вл-ті відповідних функцій), з геометрією (в темі “Координати на площині”) та з ін. Серед основ понять важливим є пон. Рівносильності: 2 р-ння наз. рівносильними, якщо кожен корінь 1го є коренем 2го і навпаки. Зауважується, що р-ння, які не мають коренів теж є рівносильними. Щодо методів розв-ня, то крім вже названих використов також умова рівності добутку чи дробу нулю, графічний метод, розкладання на множники.

15. Методика вивчення нерівностей в основній школі. Метод інтервалів.

Систематичне вивчення числових нерівностей з однією змінною та їхніх систем передбачено у 9 кл., хоча з найпростішими числовими нерівностями учні мали справу в попередніх класах, порівнюючи числа і числові вирази.

Дана змістова лінія тісно пов’язана з іншими: з функціональною(у розв-ні нерівностей та їх систем можуть використ. властивості відповідних ф-цій), з геометрією(в темі “Нерівність трикутника”)

Поняття числової нерівності вводиться у 5 кл.

Дов­гий час у шкільних підручниках обмежувались геометричним тлумаченням числової нерівності: число а називали більшим за число b, якщо точка, що зображує число а на координатній прямій, міститься праворуч від точки, що зображує число b. В процесі систематичного вивчення нерівностей у курсі алгебри формулювалось і доводилось твердження про властивість число­вих нерівностей: число а більше за число b, якщо різниця а - b -додатне число, і число а менше від числа Ь, якщо різниця а-b - від ємне число; навпаки, якщо різниця а - b - додатне число, то число а більше за число b і якщо різниця а - b - від'ємне число, то число а менше від числа Ь.

В деяких сучасних підручниках автори поверну­лись до традиційного підходу до вивчення числових нерівностей - першу частину сформульованого вище твердження прийнято як означення числової нерівності.

У 9 кл. вивчаються числові нерівності, лінійні нерівності з однією змінною та їх системи, квадратні нерівності.

Під час розв'язування лінійних нерівностей з однією змін-ною доцільно використати аналогію з рівняннями і щодо означення і щодо розв’язування.

Лінійною нерівністю з однією змінною називають нерів-ність ви­гляду ах < b або ах > b (або ах ≤ b або ах ≥ b), де х -змінна, а і b -числа. Якщо 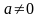то множ. розв’язків нерівн.

ах < b є або множина 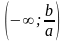, або множина . При а=0 множ. Розв’язків цієї нерівності є або множина всіх чисел (при 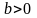) або Ø (при ).

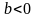Якщо то множ. розв’язків нерівн.

ах > b є або множина , або множина . При а=0 множ. розв’язків цієї нерівності є або Ø (при ) або множина всіх дійсних чисел (при ).

Вивчення нерівностей другого степеня з однією змінною перед­бачено в курсі алгебри 9 класу і по­в'язується з графіком квадратичної функції. Перш ніж розв'язувати та­кі нерівності загального вигляду, треба розглянути способи розв'язу­вання нерівностей вигляду х² < а, х²>а (відповідно х² ≤ а, х²≥ а). Саме в процесі знаходження роз­в'язків таких нерівностей частина учнів допускає помилки. 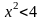Наприклад, для нерівності пишуть х < ±2, а для нерівності дістають х > ± 2 за аналогією з розв'язуванням квадратного рів­няння х² = 4, х² = ±2.

Доцільно розглянути три способи розв'язування, наприклад, нерівності х² < 4.

Графічний спосіб. Ліву і праву частини цієї нерівнос­ті задають функції у = х² і у = 4. Побудуємо в одній системі коор­динат графіки цих функцій і знайдемо множину тих значень х, за яких графік функції у = х лежить нижче, ніж графік фукнції у = 4. Такою множиною є проміжок (-2; 2), тобто - 2< х < 2.

Можна було б побудувати графік функції у = х² - 4 і знайти ті х, за яких графік міститься під віссю х.

Спосіб розкладання на множники. Перенесемо число 4 в ліву частину нерівності і розкладемо її на множники. Дістанемо х² - 4 < 0, (х - 2) (х + 2) < 0.

Добуток двох співмножників від'ємний тоді і тільки тоді, ко­ли їх знаки протилежні. Звідси можна скласти дві системи ліній­них нерівностей.

Спосіб добування арифметичного кореня з обох частин нерівності. Оскільки права частина нерівності - додатне число, то після добування кореня з обох час­тин нерівності дістаємо 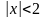. Числа, у яких модуль менший від числа 2, належить проміжку (-2; 2).

Серед методів розв-ня нер-й і сис-м нер-й центральне місце займає метод інтервалів. Поняття про метод інтервалів доцільно ввести на прикладі р.

Приклад:

Розв’язати нерівність:

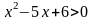
Далі можна навести приклад розв’язування дробової нерівності

Приклад:

Розв’язати нерівність: .

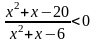В-дь: .
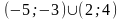