
- •1.Диференціація в навчанні математики, її особливості на сучасному етапі.
- •2.Діяльнісний підхід у навч. Мат-ки. Зміст і роль заг. Розум. Дій і прийомів розумової діялн.
- •3. Методи навчання математики.
- •4.Математичні поняття, методика їх формування
- •5.Методика вивчення теорем та їх доведень у школі.
- •6.Правила і алгоритми в шкм,методика роботи з ними.
- •7. Задачі в навчанні мат-ки. Методика навч. Учнів розвязувати матем.Задачі.
- •8. Урок математики в сучасній школі. Підготовка вчителя до уроку математики.
- •9. Методика вивчення натуральних чисел в основній школі. Формування в учнів обчислювальних умінь і навичок. Подільність чисел.
- •10.Звичайні і десяткові дроби, додатні і від'ємні числа; методика їх вивчення.
- •11. Числа та обчислення в 7- 9 класах. Наближені обчислення в основній школі. Застосування обчислювальних засобів в навчанні математики.
- •12. Методика вивчення тотожних перетворень в основній школі. Перетворення цілих виразів.
- •13. Методика вивчення тотожних перетворень в основній школі. Перетворення раціональних та ірраціональних виразів.
- •14. Методика вивчення рівнянь в основній школі. Методика вивчення
- •15. Методика вивчення нерівностей в основній школі. Метод інтервалів.
- •16. Текстові задачі в навчанні математики. Застосування методу рівнянь до розв’язування т. З. Математичне моделювання.
- •17. Функціональна лінія в основній школі. Ф-нальна пропедевтика. Методика вивчення лінійної ф-ії.
- •18.Методика вивчення окремих видів функцій у курсі алгебри 7-9 класів.
- •19.Логічна будова шкільного курсу геометрії. Методика проведення перших уроків планіметрії.
- •20.Особливості вивчення многокутників у шкільному курсі геометрії.
- •21. Методика вивчення трикутників
- •22.Паралельність і перпендикулярність прямих на площині. Методика вивчення.
- •23.Методика вивчення геометричних побудов на площині
- •24.Методика вивчення чотирикутників.
- •25.Методика вивчення декартових координат на площині .
- •26. Методика вивчення векторів на площині
- •27. Методика вивчення перетворень на площині.
- •28.Методика вивчення кола й круга,їх елементів.Вписані й описані фігури.
- •29.Поняття величини. Геометричні величини в шкільному курсі планіметрії, методика їх вивчення.
- •30.Методика вивчення початків стереометрії в основній школі.
13. Методика вивчення тотожних перетворень в основній школі. Перетворення раціональних та ірраціональних виразів.
До тотожних перетворень раціональних витворення раціональних виразів, відмінних від цілих, які вивчаються у 8 класі, належать скорочення раціональних дробів, додавання і віднімання таких дро-бів, множення, піднесення до степеня з натуральним показником, ділення дробів і тотожні перетворення раціональних виразів, до складу яких входять цілі і дробові вирази.
Під
час скорочення раціональних дробів,
що спирається на ос- новну властивість
дробу, типовою помилкою є такі: ;
;
 ;
; .
.
Одним із способів зменшення кількості названих помилок є об-числення даного й одержаного після «перетворення» виразу. Для никнення помилок треба зробити пряму вказівку про не припусти-мість таких перетворень ще при введенні нового матеріалу і пояс-нити учням, чому саме таке перетворення є помилковим.
Перетворення суми і різниці раціональних дробів з різними знаменниками спирається на вміння знаходити найпростіший
спільний знаменник.
Доцільно сформулювати правило (алгоритм) відшукання найпростішого спільного знаменника:
1) скласти добуток найменшого спільного кратного модулів коефіцієнтів знаменників даних дробів і степенів кожної змінної з найбільшим показником, з яким змінна входить до знаменників цих дробів;
2) знайти додаткові множники даних дробів; для цього досить записати спільний знаменник у вигляді добутку двох співмножників, з яких один - знаменник даного дробу, тоді другий буде додатковим множником його;
3) знайти добуток чисельника кожного дробу на додатковий множник і записати спільний знаменник.
Аналогія
у виконанні дій множення і ділення
раціональних дробів і звичайних дробів
як числових виразів полегшує сприймання
учнями цих тотожних перетворень. Разом
з тим, виконуючи перетворення, треба
враховувати, що два дробово-раціональні
вирази називаються тотожно рівними,
якщо вони мають одну й ту
саму область визначення і на ній тотожно
рівні. Тому,
перетворюючи у
дріб добуток дробів
 ,
дістанемо
дріб
,
дістанемо
дріб
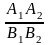 ,
який має ту саму область визначення що
і добуток
.
Отже
ці вирази тотожно рівні.
,
який має ту саму область визначення що
і добуток
.
Отже
ці вирази тотожно рівні.
Основною метою перетворення раціональних виразів, до складу яких входять цілі і дробові вирази, є перетворення їх у дріб, чисельник і знаменник якого є цілими раціональними виразами. Може трапитись так, що одержаний внаслідок перетворення дріб не тотожно рівний даному раціональному виразу внаслідок зміни області визначення. У таких випадках у відповіді разом зі знайденим дробом треба зазначати множину, на якій розглядається цей дріб.
Приклад:
Перетворити в раціональний дріб вираз
 .
Розв’язання:
.
Розв’язання:
 ;
;
 .
.
У
курсі алгебри основної школи учні
стикаються з ірраціональними виразами
(щоправда, термін не вживається) у
зв'язку з вивченням арифметичного
квадратного кореня. На цьому етапі
навчання розглядаються такі перетворення
ірраціональних виразів: перетворення
кореня із добутку, дробу, степеня,
множення і ділення коренів, винесення
множника з-під знака кореня, внесення
множника під знак кореня, звільнення
від ірраціональності в знаменнику,
зведення подібних доданків, що містять
корені. Символ
 вживається лише для арифметичних
коренів.
вживається лише для арифметичних
коренів.
Зазначимо,
що вже при вивченні коренів використовують
поняття не тільки раціонального дробу,
а й дробу
 ,
де а і b
- будь-які
вирази, у тому числі й такі, що містять
корені. Треба
мати на увазі, що в 10 класі вивчатимуться
далі ірраціональні вирази, які
містять корені будь-якого степеня і
пов'я-зані з ними степені з раціональними
показниками. Для вира-зів, що містять
корені, поняття стандартного виразу
,
де а і b
- будь-які
вирази, у тому числі й такі, що містять
корені. Треба
мати на увазі, що в 10 класі вивчатимуться
далі ірраціональні вирази, які
містять корені будь-якого степеня і
пов'я-зані з ними степені з раціональними
показниками. Для вира-зів, що містять
корені, поняття стандартного виразу
 встановлене
стосовно тих виразів, які містять ли-ше
дії множення, ділення, піднесення
до степеня і добування кореня. Якщо
вираз є раціональним
щодо виразів вигляду
,
то їх перетворення відбувається так
само, як і зведення раціональних виразів
до стандартного вигляду.
встановлене
стосовно тих виразів, які містять ли-ше
дії множення, ділення, піднесення
до степеня і добування кореня. Якщо
вираз є раціональним
щодо виразів вигляду
,
то їх перетворення відбувається так
само, як і зведення раціональних виразів
до стандартного вигляду.
У
курсі алгебри 8 класу перетворення
виразів, що містять квадратні корені,
передбачають використання означення
арифметичного кореня, тотожностей
 Тому
належну увагу треба приділити
засвоєнню суттєвих ознак квадратного
кореня, що входять в означення.
Найбільше помилок учні роблять, виносячи
з-під знака кореня числові і буквені
множники і вносячи їх під цей знак.
Для усунення формалізму в засвоєнні
навичок і умінь виконання тотожних
перетворень різних виразів треба поряд
із введенням основного завдання
перетворення (зведення до стандартного
вигляду) домагатись усвідомлення учнями
того, що у кожному конкретному випадку
метою тотожного перетворення є
подання виразу у вигляді, зручному для
розв'язування поставленої задачі.
Тому
належну увагу треба приділити
засвоєнню суттєвих ознак квадратного
кореня, що входять в означення.
Найбільше помилок учні роблять, виносячи
з-під знака кореня числові і буквені
множники і вносячи їх під цей знак.
Для усунення формалізму в засвоєнні
навичок і умінь виконання тотожних
перетворень різних виразів треба поряд
із введенням основного завдання
перетворення (зведення до стандартного
вигляду) домагатись усвідомлення учнями
того, що у кожному конкретному випадку
метою тотожного перетворення є
подання виразу у вигляді, зручному для
розв'язування поставленої задачі.
