
- •Екзаменаційний білет № 11
- •Формула Тейлора функції однієї змінної .
- •11.2 Перевiрка статистичних гiпотез. КритерiїКолмогорова та Пiрсона.
- •Екзаменаційний білет № 12
- •12.2Випадкове середнє та дисперсія. Емпiричнафункцiярозподiлу.
- •Екзаменаційний білет № 13
- •Теорема існування та єдиностi розв'язку задачi Кошiдиференцiальногорiвняння першого порядку.
- •Поняття випадкового процесу. Вiнерiвський та Пуасонiвський процеси.
- •Екзаменаційний білет № 14
- •14.1. Лiнiйнiоднорiднiдиференцiальнiрiвняння n-го порядку iз сталими коефiцiєнтами. Побудова загального розв'язку.
- •14.2. Центральна гранична теорема для однаково розподiлених незалежних випадкових величин.
- •Екзаменаційний білет № 15
- •15.1Системи лiнiйнихдиференцiальнихрiвнянь з сталими коефiцiєнтами. Знаходження загального розв'язку однорiдних систем.
- •Системилінійниходноріднихдиференціальнихрівнянь з сталимикоефіцієнтами.
- •4.3.1. Розв’язування систем однорідних рівнянь з сталими коефіцієнтами методом Ейлера.
- •Розв’язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом
- •15.2Основнi типи дискретних та неперервних розподiлiв.
- •Екзаменаційний білет № 16
- •Властивості розв’язків лінійних неоднорідних систем
- •Побудова частинного розв’язку неоднорідної системи методом варіації довільних сталих
- •Формула Коші
- •НерiвнiстьЧебишева. Закон великих чисел.
- •Екзаменаційний білет № 17
- •17.1Теорiя стiйкостi. Стiйкiстьлiнiйнихстацiонарних систем. Критерій Гурвiца. Теореми Ляпунова.
- •Фазовий портрет лінійноїсистеми на площині
- •17.2Випадковi величини. Властивостiфункцiйрозподiлу.
- •Екзаменаційний білет № 18
- •18.1Динамічні системи. Означення та класифікація динамічних систем за Калманом.
- •18.2Аксiоматичне означення ймовiрностей. Формула повної ймовiрностi та формула Байеса.
- •Екзаменаційний білет № 19
- •Задача однофакторного дисперсійного аналізу та її розв’язання.
- •19.2Первинні оператори. Оператор присвоєння. Структурні оператори (складені, умовні, циклічні). Оператор вводу-виводу.
- •Екзаменаційний білет № 20
- •Градiєнт, дивiргенцiя I вихор векторного поля.
- •20.2 Слабко-ефективні альтернативи. Теорема Гермейєра.
17.2Випадковi величини. Властивостiфункцiйрозподiлу.
Нехай
маємо ймовірносний простір (
,
F, P).
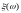 -
деяка функція, визначена на
.
-
деяка функція, визначена на
.
Озн. -буде вимірною функцією, якщо
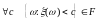 ,
де F
,
де F
 алгебра.
алгебра.
Озн.
Вимірна функція
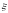 -
випадкова величина ,
-
випадкова величина ,
 .
.
Озн.
F(x)=
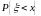 - функція розподілу випадкової величини
.
- функція розподілу випадкової величини
.
Властивості функцій розподілу.
1. F(x) – невід’ємна
2. F(x) - монотонно неспадна.(x1>=x2 => F(x1)>=F(x2) )Справді:
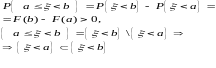 Отже
Отже
3. F(x) - неперервна зліва. Тобто F(x-0) = F(x)
4.
Нормованою F(- )
= 0 , F(+
)
= 1.
)
= 0 , F(+
)
= 1.
Дискретні випадкові величини.
Нехай
<>
ймовірнісний простір. Дискретноювипадковою
величиною називається функція
на ,
яка набуває скінченне або зліченне
число значень х1,
х2,
…, хn,
… і є вимірною відносно
алгебри .
Це означає, що для кожного хі{
: x}
(1).Дійсно, якщо для функції
має місце співвідношення (1), то ця
функція вимірна відносно ,
так як для кожного дійсного х {
: x}=
 {
: xі}
.
Крім того, якщо
вимірна відносно
алгебри ,
то за Теоремою 1 для кожного дійсного х
{
: x
} .
Таким чином, якщо
дискретна випадкова величина на
ймовірнісному просторі <>,
яка приймає значення х1,
х2,
…, хn,
…, то для кожного n визначена ймовірність
Рn=Р{
: xn}
Нехай
()
– дискретна випадкова величина, яка
набуває значення х1,…,
хі,….
Набір чисел Р{:()=xi}=pi(i=1,2,…)
називають
розподілом випадкової величини .
Зрозуміло, що рі
0,
{
: xі}
.
Крім того, якщо
вимірна відносно
алгебри ,
то за Теоремою 1 для кожного дійсного х
{
: x
} .
Таким чином, якщо
дискретна випадкова величина на
ймовірнісному просторі <>,
яка приймає значення х1,
х2,
…, хn,
…, то для кожного n визначена ймовірність
Рn=Р{
: xn}
Нехай
()
– дискретна випадкова величина, яка
набуває значення х1,…,
хі,….
Набір чисел Р{:()=xi}=pi(i=1,2,…)
називають
розподілом випадкової величини .
Зрозуміло, що рі
0,
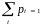 .
.
Функція розподілу дискретної випадкової величини () визначається рівністю

Сумісний розподіл випадкових величин() і (). Нехай () – дискретна випадкова величина, яка набуває значень х1, х2,…, хі,…,() – дискретна випадкова величина, яка набуває значень y1, y2,…, yі,…. Набір чисел Р{:()=xi, ()=yi}=pij(i=1, 2, …; j=1, 2, …) називається сумісним розподілом випадкових величин і (розподілом випадкового вектора (, )). Мають місце такі твердження:
а)
рij0,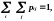
б)
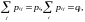 де {pi}
розподіл (),
{qi}
– розподіл ().
де {pi}
розподіл (),
{qi}
– розподіл ().
Незалежні випадкові величини. Випадкові величини і н а з и в а ю т ь с я н е з а л е ж н и м и, якщо для будь-яких i j
P{()=xi, ()= yi} = P{()=xi} P{()= yi}.
Математичне сподівання випадкової величини. Нехай () – дискретна випадкова величина, яка набуває значень хі з імовірностямирі(і=1, 2, …). Припустимо, що ряд хірі збігається. Тоді м а т е м а т и ч н и м с п оді-
в
а н н я м випадкової величини ()
називається сума ряду М
()
=
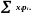 Якщо
хірі=+,
то кажуть, що випадкова величина ()
не має математичного сподівання.
Математичне сподівання суми випадкових
величин дорівнює сумі математичних
сподівань.
Якщо
хірі=+,
то кажуть, що випадкова величина ()
не має математичного сподівання.
Математичне сподівання суми випадкових
величин дорівнює сумі математичних
сподівань.
Дисперсія випадкової величини () визначається рівністю
D=M[-
M]2=
M2-(
M)2=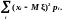
Властивості дисперсії.
D=0
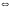 =соnst;
=соnst;D=

D(C)=c2 D;
D(
 C)=
D
.
C)=
D
.Якщо та
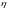 незалежні випадкові величини, то D(
)=
D
+D
.
незалежні випадкові величини, то D(
)=
D
+D
.
Коєфіцієнтковаріаціївипадкових величин та це: cov(, )=M(-M)(-M).
Коефіцієнт кореляції. К о є ф і ц і є н т о м к о р е л я ц і ї випадкових величин і називаються
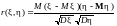
Мають місце такі твердження:
а) r(, ) 1;
б) якщо і незалежні, то r(, )=0;
в) якщо r(, )=1, то з імовірністю одиниця =а+b, де а і b – деякі сталі.
