Екзаменаційний білет № 11

1. Формула Тейлора функції однієї змінної .

Теорема 1 (локальна формула Тейлора).

Нехай функція 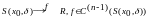і

– локальна формула Тейлора. (1)

де - залишковий член у формі Пеана.

Розглянемо дві функції:

;

, ;

,

,

формула (1).

У випадку х₀=0 формула Тейлора називається формулою Маклорена: (2).

Теорема 2 (формула Тейлора).

Якщо fCⁿ[a,b] і  f⁽ⁿ⁺¹⁾, x(a,b),то для двох довільних точок х та х₀ з [a,b] має місце формула (5), яка називається формулою Тейлора із залишковим членом (6) у формі Шльоміха-Рома.

(5),

де (6).

Розглянемо функцію [a,b] R; fCⁿ[a,b] і  f⁽ⁿ⁺¹⁾, x(a,b) і , де t[a,b], а х – деяка стала з [a,b], параметр р – довільний, додатній,  – деяка стала.

h(x)=0, x₀[a,b] і знайдемо h(x₀): .

Виберемо  таке, щоб h(x₀)=0.

Знайдемо похідну:

.

 . Тоді вірні формули (5) та (6).

Підставляючи різні значення р, можна отримати різні залишкові членів:

1. р=1 –залишк член у формі Коші;

2. р=n+1 – залишковий член у формі Лагранжа.

3. Якщо , тоді – залишковий член у формі Коші для формули Маклорена.

4. – залишковий член у формі Лагранжа для формули Маклорена.

5. Якщо h=x-x0, тоді: – формула Тейлора у диференційованому вигляді.

11.2 Перевiрка статистичних гiпотез. КритерiїКолмогорова та Пiрсона.

Задача перевірки гіпотез відноситься до 3-го типу задач мат. статистики. Ця задача полягає у визначенні на основі спостережень узгодженності наявної інформації з тим чи іншим припущенням про значення невідомого параметру . Існує два типи гіпотез, що перевіряються:

1. типу альтернативного вибору;

2. типу .

Альтернативний вибір.

У задачі перевірки гіпотез типу АВ формулюються два припущення, щодо можливості значення невідомого параметру . Ці припущення позначаються як та . На основі виборки , треба сформулювати правило, яке б робило вибір на користь тієї чи іншої гіпотези.

Оскільки кожна серія спостережень дає нову вибірку,то висновки про ту чи іншу гіпотезу ( що базуються на основі правила ) будуть носити випадковий характер. Отже, в задачі АВ вводять додаткову характеристику: довірчу ймовірність - ймовірність прийняття гіпотези , коли вона є справедливою.

Більш формально: , , , .

В задачі АВ необхідно з двох однотипних припущень та про значення параметру вибрати одне . Ймовірність вибору першого, коли воно дійсно вірне , повинна бути , а також ймовірність відхилення другого, якщо насправді воно справедливе, повинна бути мінімальною. Ці дві ймовірності в математичній статистиці прийнято називати похибками першого та другого роду відповідно. Тобто необхідно прийняти рішення при фіксованій похибці першого роду і так , щоб похибка другого роду була мінімальною.

Типу .

У задачі перевірки гіпотези типу висувається наступна гіпотеза: і її альтернатива: . Отже у цьому типі гіпотез на відміну від попередньго випадку, основна гіпотеза і альтернативна є різними за типом : - одинична та - множинна .

Отже в цій задачі треба із імовірністю підтвердити припущення , коли воно є вірним чи відхилити його.

Критерій Смірнова-Колмогорова.

Цей критерій застосовується для перевірки гіпотез типу , які мають форму припущення про вигляд функції розподілу.

Маємо вибірку з геральної сукупності

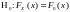, де - будь-яка задана, тобто функція розподілу перевіряється на співпадання з заданою.

Алгоритм критерію:

1. Будуємо статистику , де - емпірична функція розподілу. Тоді справедлива

Теорема. (Колмогорова).

Якщо вибірка була побудована з функцією розподілу ( повинна бути неперервною), тобто має місце наше припущення, то

. Тобто якщо припущення зроблено не правильно, то данної границі , взагалі кажучи, може не існувати.

2. По вибранному знаходимо : , далі - довірча область для .

1. Приймаємо рішення в залежності від справедливості співвідношення : : + - приймається

- - відхиляється

Критерій (Пірсона).

Цей критерій застосовуєьтся для перевірки гіпотез для групованих вибірок.

Озн. Групована вибірка - це представлення вихідної вибірки у вигляді розбиття на групи, що не мають спільних елементів і охоплюють всю вибірку. Висувається ознака кожної з груп і кількість елементів (абсолютна частота) у кожній групі. Ознаками групування (груп) у дискретному випадку є можливі значення спостережень, у неперервному - інтервали можливих значень спостережень.

Гіпотеза, до якої застосовується вказаний критерій, має вигляд припущень про ймовірність належності будь-якій з груп групованої вибірки:

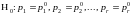
належить першій групі

Алгоритм критерію.

1. Статистика критерію: , де

- абсолютні кількості віднесення до i-ї групи у відповідності з припущенням гіпотези;

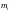- абсолютна частота;

- характеристика розходження наявної абсолютної частоти кожної групи і передбачуваної у відповідності з припущенням гіпотези.

Твердження про розподіл статистики має асимптотичних характер: розподіл _N при співпадає з .

Іноді користуються модифікованим твердженням про вигляд граничного розподілу.

Він має вигляд , де - кількість груп, - кількість невідомих параметрів , що ,залежать від цих параметрів.

Алгоритм подальших дій у критерії співпадає із звичайними кроками критерію згоди:

2. - довірча область;

3. : + - приймається

- - відхиляється