
- •Математичні методи
- •Мета застосування математичних методів у соціології: опис, пояснення та прогнозування соціальних процесів та явищ.
- •2. Логіка та основні етапи аналізу соціологічних даних.
- •3. Статистичні методи аналізу даних та задачі, що розв’язуються з їх застосуванням.
- •4. Вимірювання.
- •6. Шкала вимірювання, типи шкал.
- •Які математичні операції можна застосовувати до метричних ознак?
- •Які математичні перетворення можна застосовувати до порядкових ознак?
- •Які математичні операції можна застосовувати до номінальних ознак?
- •9. Характеристики форми розподілу.
- •10. Міри центральної тенденції та міри варіації.
- •11. Аналіз таблиць двомірного розподілу.
- •13. Обчислення коефіцієнту "хі-квадрат" Пірсона.
- •14. Коефіцієнти зв’язку, побудовані на основі "хі-квадрат".
- •18. Функціональний та кореляційних зв’язок.
- •19. Діаграма розсіяння.
- •20. Лінійний та нелінійних зв’язок.
- •21. Коефіцієнт кореляції Пірсона: правила обчислення та інтерпретації. Кореляційне відношення.
- •Як інтерпретуються коефіцієнти регресії в рівнянні лінійної регресії?
- •25. Лінійна парна регресія: побудова, запис та інтерпретація рівняння регресії. Множинна лінійна регресія, інтерпретація коефіцієнтів рівняння множинної лінійної регресії.
- •Запишіть загальний вигляд рівняння регресії.
- •Як інтерпретується коефіцієнт множинної кореляції?
- •Як інтерпретується коефіцієнт множинної кореляції?
- •27. Якість рівняння регресії, коефіцієнт детермінації.
- •Які Ви знаєте підходи до оцінювання якості рівняння регресії?
- •Як обчислюється і який зміст має коефіцієнт детермінації?
- •28. Класифікація статистичних мір за рівнем соціологічного вимірювання. Графічне представлення соціологічних даних: гістограма, полігон, огіва, кумулята. Графічне зображення даних
- •29. Діаграми: секторні, стовпчикові, рядкові.
- •30. Планування вибірки
- •31. Репрезентативність вибірки.
- •33. Обчислення обсягу вибірки за значенням припустимої похибки.
- •34. Проста випадкова вибірка
- •35. Багатоступенева вибірка.
- •37. Способи ремонту вибірки: відсікання, перезважування.
- •42. Поняття статистичної гіпотези.
- •43. Нульова та альтернативна гіпотези.
- •44. Помилки першого та другого роду.
- •45. Статистичні критерії.
- •46. Загальна процедура перевірки статистичних гіпотез.
- •47, 48, 49.Факторний аналіз. Застосування факторного аналізу в емпіричних соціологічних дослідженнях.
- •Задачи и условия факторного анализа
- •Процедура вращения. Выделение и интерпретация факторов
42. Поняття статистичної гіпотези.
Нехай
у (статистичному) експерименті
спостерігається реалізація
![]() деякої
випадкової
величини
X,
розподіл
якої
деякої
випадкової
величини
X,
розподіл
якої
![]() невідомий
повністю чи частково. Тоді будь-яке
твердження, що стосується
,
називається статистичною
гіпотезою.
Гіпотези розрізняються за видом
припущень, що містяться в них:
невідомий
повністю чи частково. Тоді будь-яке
твердження, що стосується
,
називається статистичною
гіпотезою.
Гіпотези розрізняються за видом
припущень, що містяться в них:
Статистична гіпотеза, що однозначно визначає розподіл , тобто
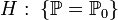 ,
де
,
де
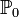 якийсь
конкретний закон, що має назву простий.
якийсь
конкретний закон, що має назву простий.Статистична гіпотеза, що стверджує, що розподіл належить до деякої сім'ї розподілів, тобто виду
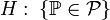 ,
де
,
де
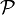 -
сім'ю розподілів, що має назву складна.
-
сім'ю розподілів, що має назву складна.
На практиці зазвичай потрібно перевірити якусь конкретну і, як правило, просту гіпотезу H0. Таку гіпотезу прийнято називати нульовою. При цьому паралельно розглядається гіпотеза, що протирічить їй H1, що називається конкуруючою або альтернативною.
Висунута гіпотеза потребує перевірки, яка здійснюється статистичними методами, тому гіпотезу називають статистичною. Для перевірки гіпотези використовують критерії, що дозволяють прийняти або спростувати гіпотезу.
В
більшості випадків статистичні критерії
засновані на випадковій вибірці
![]() фіксованого
об'єму
фіксованого
об'єму
![]() з
розподілу
з
розподілу
![]() .
У послідовному аналізі вибірка формується
в ході самого експерименту і тому її
об'єм є випадковим величиною.
.
У послідовному аналізі вибірка формується
в ході самого експерименту і тому її
об'єм є випадковим величиною.
[ред.] Приклад
Нехай
дано незалежну вибірку
![]() з
нормального
розподілу,
де μ — невідомий параметр. Тоді
з
нормального
розподілу,
де μ — невідомий параметр. Тоді
![]() ,
де μ0
— фіксована стала, є простою гіпотезою,
а альтернативна до неї
,
де μ0
— фіксована стала, є простою гіпотезою,
а альтернативна до неї
![]() —
складною.
—
складною.
Етапи перевірки статистичних гіпотез
Формулювання основної гіпотези H0 і конкуруючої гіпотези H1. Гіпотези повинні бути чітко формалізовані в математичних термінах.
Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези.
Розрахунок статистики φ критерію такий, що:
її величина залежить від початкової вибірки
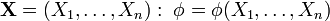 ;
;по її значенню можна зробити висновки про істинність гіпотези H0;
сама статистика φ повинна підкорятися якомусь невідомому закону розподілу, так як сама φ є випадковою в силу випадковості
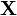 .
.
Побудова критичної області. З області значень φ виділяємо підмножину
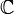 таких
значень, по яким можна судити про
суттєвість розбіжностей з припущенням.
Її розмір вибирається таким чином, щоб
виконувалась рівність
таких
значень, по яким можна судити про
суттєвість розбіжностей з припущенням.
Її розмір вибирається таким чином, щоб
виконувалась рівність
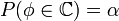 .
Ця множина
і
називається критичною
областю.
.
Ця множина
і
називається критичною
областю.Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику φ і по попаданню (або непопаданню) в критичну область виноситься ухвала про відкидання (або ухвалення) висунутої гіпотези H0.
Види критичної області
Д вобічна критична область визначається двома інтервалами
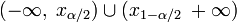 ,
де
,
де
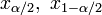 знаходять
з умов
знаходять
з умов
 .
.
Лівобічна
критична область
визначається інтервалом
![]() ,
де xα
знаходять з умови P(φ
< xα)
= α.
,
де xα
знаходять з умови P(φ
< xα)
= α.
Правобічна
критична
область визначається інтервалом
![]() ,
де x1
− α
знаходять з умови P(φ
< x1
− α)
= 1 − α.
,
де x1
− α
знаходять з умови P(φ
< x1
− α)
= 1 − α.
2. Поняття статистичної гіпотези та її вигляд Статистичною гіпотезою називається будь-яке твердження про вигляд або властивості розподілу випадкових величин, що спостерігаються в експерименті. Правило, згідно з яким гіпотеза Н0, що перевіряється, приймається чи відхиляється, називається статистичним критерієм для перевірки гіпотези Н0. Наведемо декілька прикладів статистичних гіпотез. 1. Гіпотеза про вигляд розподілу. Нехай о = (о1, о2, ..., оn) — вибірка з генеральної сукупності з невідомою функцією розподілу Fо(х). Тоді Н0: Fо(х) = F(X), де F(x) повністю задана, або Н0: Fо(х) є М, де М = {Fо(х, и), и є И} — задане сімейство функцій розподілу. 2. Гіпотеза однорідності. Нехай маємо k вибірок о = (о1, о2, ..., оn), і = 1, k з генеральних сукупностей з функціями розподілу Fі(х), і = 1, k. Потрібно перевірити гіпотезу про те, що це спостереження над однією і тією ж випадковою величною, тобто Н0: F1(х) ? F2(х) ? ... ? Fk(x). 3. Гіпотеза незалежності. Одночасно спостерігаються дві випадкові величини о та з, F(о,з)(х, у) — невідома їхня сумісна функція розподілу. Потрібно перевірити гіпотезу про те, що о та з — незалежні випадкові величини, тобто Н0: F(о,з)(х, у) = Fо,(х) Fз(у).
